experimental probability algebra meaning

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Prob. distribution

Experimental prob.

Experimental probability

Here you will learn about experimental probability, including using the relative frequency and finding the probability distribution.

Students will first learn about experimental probability as part of statistics and probability in 7 th grade.

What is experimental probability?

Experimental probability is the probability of an event happening based on an experiment or observation.

To calculate the experimental probability of an event, you calculate the relative frequency of the event.

Relative frequency =\cfrac{\text{frequency of event occurring}}{\text{total number of trials of the experiment}}

You can also express this as R=\cfrac{f}{n} where R is the relative frequency, f is the frequency of the event occurring, and n is the total number of trials of the experiment.

If you find the relative frequency for all possible events from the experiment, you can write the probability distribution for that experiment.

The relative frequency, experimental probability, and empirical probability are the same thing and are calculated using the data from random experiments. They also have a key use in real-life problem-solving.

For example, Jo made a four-sided spinner out of cardboard and a pencil.

She spun the spinner 50 times. The table shows the number of times the spinner landed on each of the numbers 1 to 4. The final column shows the relative frequency.

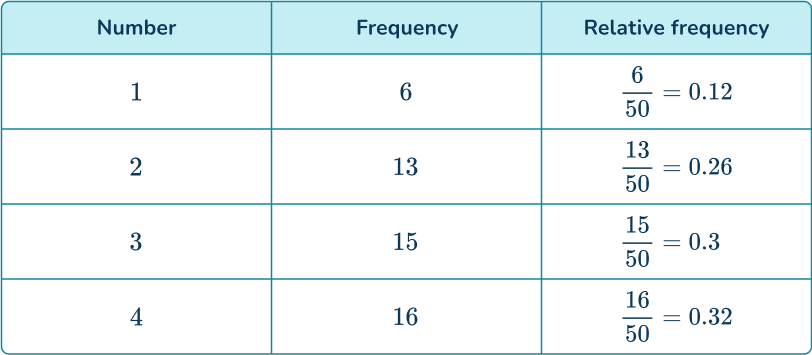
The relative frequencies of all possible events will add up to 1.

This is because the events are mutually exclusive.

See also: Mutually exclusive events

[FREE] Probability Check for Understanding Quiz (Grade 7 to 12)

Use this quiz to check your grade 7 to 12 students’ understanding of probability. 15+ questions with answers covering a range of 7th to 12th grade probability topics to identify areas of strength and support!

Experimental probability vs theoretical probability

You can see that the relative frequencies are not equal to the theoretical probabilities you would expect if the spinner was fair.

If the spinner is fair, the more times an experiment is done, the closer the relative frequencies should be to the theoretical probabilities.

In this case, the theoretical probability of each section of the spinner would be 0.25, or \cfrac{1}{4}.

Step-by-step guide: Theoretical probability

Common Core State Standards

How does this relate to 7 th grade math?

• Grade 7 – Statistics & Probability (7.SP.C.5) Understand that the probability of a chance event is a number between 0 and 1 that expresses the likelihood of the event occurring. Larger numbers indicate greater likelihood. A probability near 0 indicates an unlikely event, a probability around \cfrac{1}{2} indicates an event that is neither unlikely nor likely, and a probability near 1 indicates a likely event.

How to find an experimental probability distribution

In order to calculate an experimental probability distribution:

Draw a table showing the frequency of each outcome in the experiment.

Determine the total number of trials.

Write the experimental probability (relative frequency) of the required outcome(s).

Experimental probability examples

Example 1: finding an experimental probability distribution.

A 3- sided spinner numbered 1, \, 2, and 3 is spun and the results are recorded.

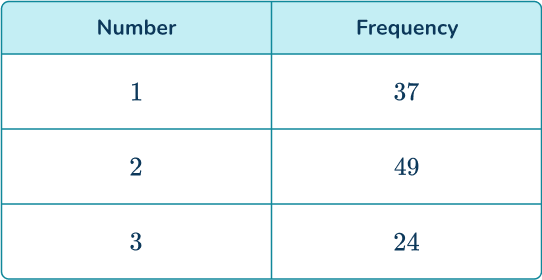
Find the probability distribution for the 3- sided spinner from these experimental results.

A table of results has already been provided. You can add an extra column for the relative frequencies.

2 Determine the total number of trials.

3 Write the experimental probability (relative frequency) of the required outcome(s).

Divide each frequency by 110 to find the relative frequencies.

Example 2: finding an experimental probability distribution

A normal 6- sided die is rolled 50 times. A tally chart was used to record the results.

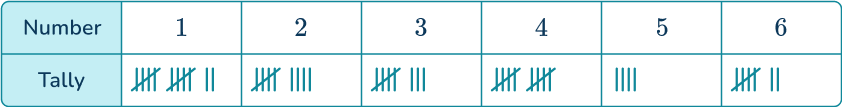
Determine the probability distribution for the 6- sided die. Give your answers as decimals.

Use the tally chart to find the frequencies and add a row for the relative frequencies.

The question stated that the experiment had 50 trials. You can also check that the frequencies add up to 50.

Divide each frequency by 50 to find the relative frequencies.

Example 3: using an experimental probability distribution

A student made a biased die and wanted to find its probability distribution for use in a game. They rolled the die 100 times and recorded the results.

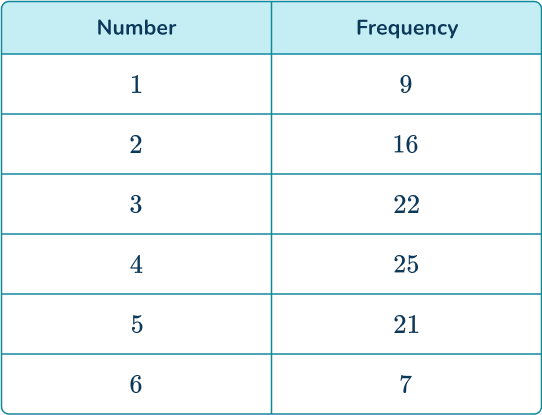
By calculating the probability distribution for the die, determine the probability of the die landing on a 3 or a 4.

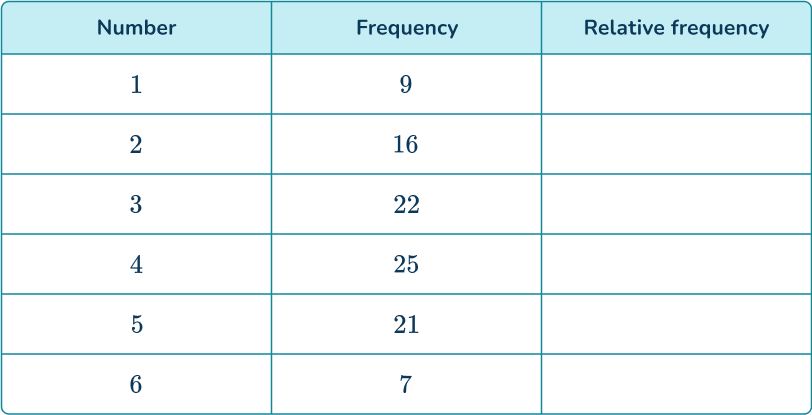
The die was rolled 100 times.

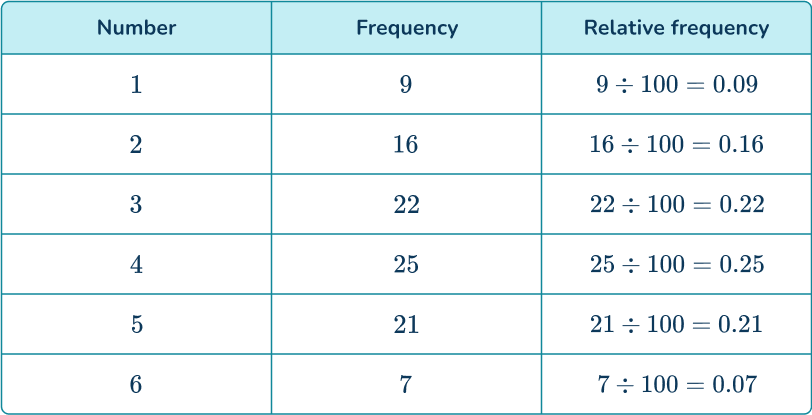
You can find the probability of rolling a 3 or a 4 by adding the relative frequencies for those numbers.

P(3\text{ or }4)=0.22+0.25=0.47

Note: P(\text{Event }A) means the probability of event A occurring.

Alternatively, it is only necessary to calculate the relative frequencies for the desired events but by calculating all of the relative frequencies and finding the sum of these values, your solution should equal 1.

The frequency of rolling a 3 or a 4 is 22+25=47.

As the total frequency is 100, the relative frequency is \cfrac{47}{100}=0.47.

Example 4: calculating the relative frequency without a known frequency of outcomes

A research study asked 1,200 people how they commute to work. 640 travel by car, 174 use the bus, and the rest walk. Determine the relative frequency of someone walking to work.

Writing the known information into a table, you have

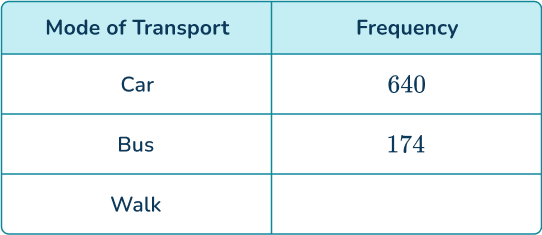
You currently do not know the frequency of people who walk to work. You can calculate this as you know the total frequency.

The number of people who walk to work is equal to

1200-(640+174)=386.

You now have the full table,

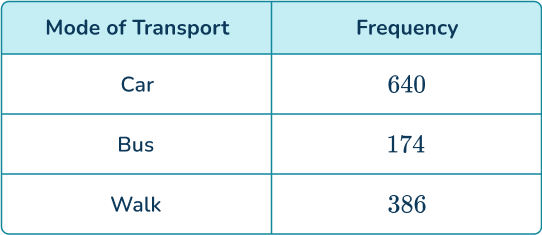
The total frequency is 1,200.

Divide each frequency by the total number of people (1,200), you have

The relative frequency of someone walking to work is 0.3216.

How to find a frequency using an experimental probability

In order to calculate a frequency using an experimental probability:

Determine the experimental probability of the event.

Multiply the total frequency by the experimental probability.

Example 5: calculating a frequency

A dice was rolled 300 times. The experimental probability of rolling an even number is \cfrac{27}{50}. How many times was an even number rolled?

The experimental probability is \cfrac{27}{50}.

An even number was rolled 162 times.

Example 6: calculating a frequency

A bag contains different colored counters. A counter is selected at random and replaced back into the bag 240 times. The probability distribution of the experiment is given below.

Determine the total number of times a blue counter was selected.

As the events are mutually exclusive, the sum of the probabilities must be equal to 1.

This means that you can determine the value of x.

1-(0.4+0.25+0.15)=0.2

The experimental probability (relative frequency) of a blue counter is 0.2.

Multiplying the total frequency by 0.2, you have

240 \times 0.2=48

A blue counter was selected 48 times.

Teaching tips for experimental probability

• Relate probability to everyday situations, such as the chance of getting heads or tails when flipping a fair coin, to make the concept more tangible.
• Rather than strictly using worksheets, let students conduct their own experiments, such as rolling dice or drawing marbles from a bag, to collect data and compute probabilities.
• Emphasize that in mathematics, experimental probability is based on actual trials or experiments, as opposed to theoretical probability which is based on possible outcomes.
• Teach students how to record the results of an experiment systematically and use them to calculate probabilities. Use charts or tables to help visualize the data.
• Discuss events that cannot occur, such as rolling a 7 with a single six-sided die. Explain that the probability of impossible events is always 0. This helps students understand the concept of probability in a broader context.

Easy mistakes to make

• Forgetting the differences between theoretical and experimental probability It is common to forget to use the relative frequencies from experiments for probability questions and use the theoretical probabilities instead. For example, they may be asked to find the probability of a die landing on an even number based on an experiment and the student will incorrectly answer it as 0.5.
• Thinking the relative frequency is an integer The relative frequency is the same as the experimental probability. This value is written as a fraction, decimal, or percentage, not an integer.
• Assuming future results will be the same Students might think that if an experiment yields a certain probability on one day, the results will be the same the next day. Explain that while probabilities are consistent over time in theory, each set of trials can have different outcomes due to randomness, and variations can occur from day to day.

Related probability distribution lessons

• Probability distribution
• Expected frequency

Practice experimental probability questions

1. A coin is flipped 80 times and the results are recorded.

Determine the probability distribution of the coin.

As the number of tosses is 80, dividing the frequencies for the number of heads and the number of tails by 80, you have

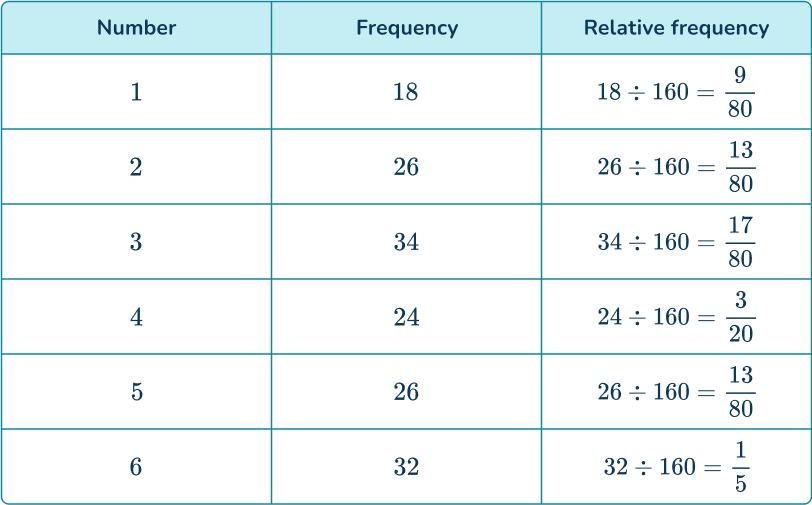
2. A 6- sided die is rolled 160 times and the results are recorded.

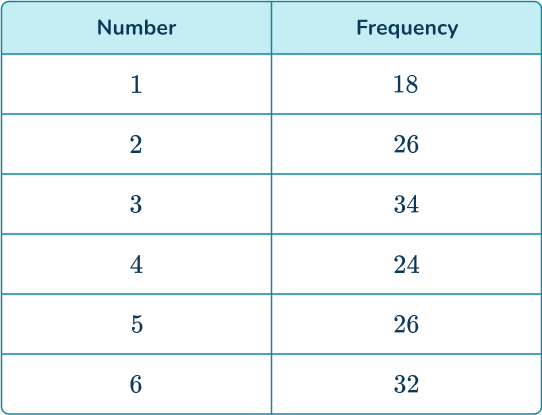
Determine the probability distribution of the die. Write your answers as fractions in their simplest form.

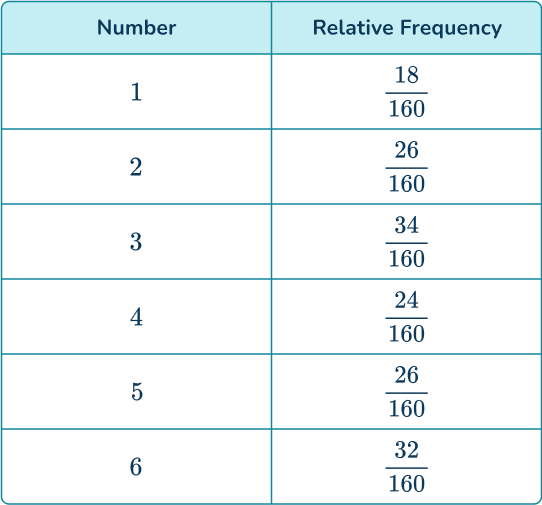
Dividing the frequencies of each number by 160, you get

3. A 3- sided spinner is spun and the results are recorded.

Find the probability distribution of the spinner, giving your answers as decimals to 2 decimal places.

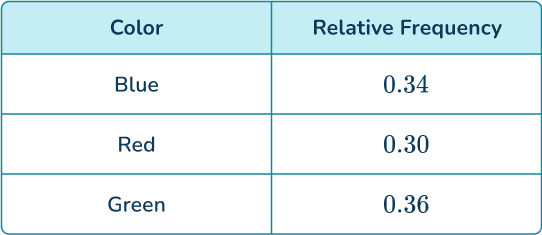
By dividing the frequencies of each color by 128 and simplifying, you have

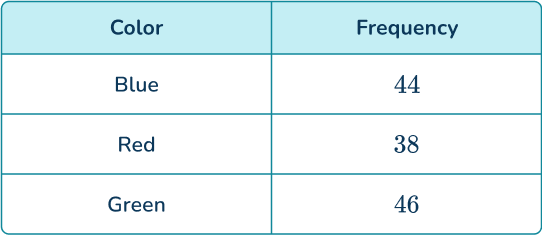
4. A 3- sided spinner is spun and the results are recorded.

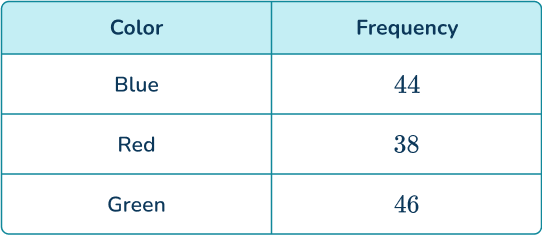
Find the probability of the spinner not landing on red. Give your answer as a fraction.

Add the frequencies of blue and green and divide by 128.

5. A card is picked at random from a deck and then replaced. This was repeated 4,000 times. The probability distribution of the experiment is given below.

How many times was a club picked?

6. Find the missing frequency from the probability distribution.

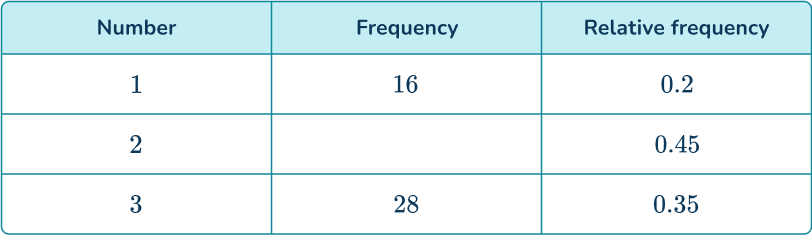
The total frequency is calculated by dividing the frequency by the relative frequency.

Experimental probability FAQs

Experimental probability is the likelihood of an event occurring based on the results of an actual experiment or trial. It is calculated as the ratio of the number of favorable outcomes to the total number of trials.

To calculate experimental probability, you calculate the relative frequency of the event: \text{Relative frequency}=\frac{\text{Frequency of event occurring}}{\text{Total number of trials of the experiment}}

Experimental Probability is based on actual results from an experiment or trial. Theoretical Probability is based on the possible outcomes of an event, calculated using probability rules and formulas without conducting experiments.

It helps us understand how likely events are in real-world scenarios based on actual data. For example, it can be used to predict outcomes in various fields such as social science, medicine, finance, and engineering.

The next lessons are

• Units of measurement
• Represent and interpret data

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Experimental Probability – Explanation & Examples

JUMP TO TOPIC

What is experimental probability? 

Practice questions, experimental probability – explanation & examples.

Experimental probability is the probability determined based on the results from performing the particular experiment. 

In this lesson we will go through:

• The meaning of experimental probability
• How to find experimental probability

The ratio of the number of outcomes favorable to an event to the total number of trials of the experiment.

Experimental Probability can be expressed mathematically as: 

$P(\text{E}) = \frac{\text{number of outcomes favorable to an event}}{\text{total number of trials of the experiment}}$

Let’s go back to the die tossing example. If after 12 throws you get one 6, then the experimental probability is $\frac{1}{12}$.  You can compare that to the theoretical probability. The theoretical probability of getting a 6 is $\frac{1}{6}$. This means that in 12 throws we would have expected to get 6 twice. 

Similarly, if in those 12 tosses you got a 1 five times, the experimental probability is $\frac{5}{12}$. 

How do we find experimental probability?

Now that we understand what is meant by experimental probability, let’s go through how it is found. 

To find the experimental probability of an event, divide the number of observed outcomes favorable to the event by the total number of trials of the experiment. 

Let’s go through some examples. 

Example 1:  There are 20 students in a class. Each student simultaneously flipped one coin. 12 students got a Head. From this experiment, what was the experimental probability of getting a head?

Number of coins showing Heads: 12

Total number of coins flipped: 20

$P(\text{Head}) = \frac{12}{20} = \frac{3}{5}$ 

Example 2:  The tally chart below shows the number of times a number was shown on the face of a tossed die. 

a. What was the probability of a 3 in this experiment?

b. What was the probability of a prime number?

First, sum the numbers in the frequency column to see that the experiment was performed 30 times. Then find the probabilities of the specified events. 

a. Number of times 3 showed = 7

Number of tosses = 30

$P(\text{3}) = \frac{7}{30}$ 

b. Frequency of primes = 6 + 7 + 2 = 15

Number of trials = 30 

$P(\text{prime}) = \frac{15}{30} = \frac{1}{2}$

Experimental probability can be used to predict the outcomes of experiments. This is shown in the following examples. 

Example 3: The table shows the attendance schedule of an employee for the month of May.

a. What is the probability that the employee is absent? 

b. How many times would we expect the employee to be present in June?

a. The employee was absent three times and the number of days in this experiment was 31. Therefore:

$P(\text{Absent}) = \frac{3}{31}$

b.  We expect the employee to be absent

$\frac{3}{31} × 30 = 2.9 ≈ 3$ days in June 

Example 4:  Tommy observed the color of cars owned by people in his small hometown. Of the 500 cars in town, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were grey. 

a. What is the probability that a car is red?

b. If a new car is bought by someone in town, what color do you think it would be? Explain. 

a. Number of red cars = 50 

Total number of cars = 500 

$P(\text{red car}) = \frac{50}{500} = \frac{1}{10}$ 

b. Based on the information provided, it is most likely that the new car will be black. This is because it has the highest frequency and the highest experimental probability. 

Now it is time for you to try these examples. 

The table below shows the colors of jeans in a clothing store and their respective frequencies. Use the table to answer the questions that follow.

• What is the probability of selecting a brown jeans?
• What is the probability of selecting a blue or a white jeans?

On a given day, a fast food restaurant notices that it sold 110 beef burgers, 60 chicken sandwiches, and 30 turkey sandwiches. From this observation, what is the experimental probability that a customer buys a beef burger?

Over a span of 20 seasons, a talent competition notices the following. Singers won 12 seasons, dancers won 2 seasons, comedians won 3 seasons, a poet won 1 season, and daring acts won the other 2 seasons. 

a. What is the experimental probability of a comedian winning  a season?

b. From the next 10 seasons, how many winners do you expect to be dancers?

Try this at home! Flip a coin 10 times. Record the number of tails you get. What is your P(tail)?

Number of brown jeans = 25

Total Number of jeans = 125

$P(\text{brown}) = \frac{25}{125}  = \frac{1}{5}$

Number of jeans that are blue or white = 75 + 20 = 95

$P(\text{blue or white}) = \frac{95}{125} = \frac{19}{25}$

Number of beef burgers = 110 

Number of burgers (or sandwiches) sold = 200 

$P(\text{beef burger}) = \frac{110}{200} = \frac{11}{20}$ 

a. Number of comedian winners = 3

Number of seasons = 20 

$P(\text{comedian}) = \frac{3}{20}$ 

b. First find the experimental probability that the winner is a dancer. 

Number of winners that are dancers = 2 

$P(\text{dancer}) = \frac{2}{20} = \frac{1}{10}$ 

Therefore we expect 

$\frac{1}{10} × 10 = 1$ winner to be a dancer in the next 10 seasons.

To find your P(tail) in 10 trials, complete the following with the number of tails you got. 

$P(\text{tail}) = \frac{\text{number of tails}}{10}$ 

Previous Lesson  |  Main Page | Next Lesson

• Math Article
• Experimental Probability

You and your 3 friends are playing a board game. It’s your turn to roll the die and to win the game you need a 5 on the dice. Now, is it possible that upon rolling the die you will get an exact 5? No, it is a matter of chance. We face multiple situations in real life where we have to take a chance or risk. Based on certain conditions, the chance of occurrence of a certain event can be easily predicted. In our day to day life, we are more familiar with the word ‘ chance and probability ’. In simple words, the chance of occurrence of a particular event is what we study in probability. In this article, we are going to discuss one of the types of probability called  “Experimental Probability” in detail.

What is Probability?

Probability, a branch of Math that deals with the likelihood of the occurrences of the given event. The probability values for the given experiment is usually defined between the range of numbers. The values lie between the numbers 0 and 1. The probability value cannot be a negative value. The basic rules such as addition, multiplication and complement rules are associated with the probability.

Experimental Probability Vs Theoretical Probability

There are two approaches to study probability:

• Theoretical Probability

What is Experimental Probability?

Experimental probability, also known as Empirical probability, is based on actual experiments and adequate recordings of the happening of events. To determine the occurrence of any event, a series of actual experiments are conducted. Experiments which do not have a fixed result are known as random experiments. The outcome of such experiments is uncertain. Random experiments are repeated multiple times to determine their likelihood. An experiment is repeated a fixed number of times and each repetition is known as a trial. Mathematically, the formula for the experimental probability is defined by;

Probability of an Event P(E) = Number of times an event occurs / Total number of trials.

What is Theoretical Probability?

In probability, the theoretical probability is used to find the probability of an event. Theoretical probability does not require any experiments to conduct. Instead of that, we should know about the situation to find the probability of an event occurring. Mathematically, the theoretical probability is described as the number of favourable outcomes divided by the number of possible outcomes.

Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.

Experimental Probability Example

Example: You asked your 3 friends Shakshi, Shreya and Ravi to toss a fair coin 15 times each in a row and the outcome of this experiment is given as below:

Calculate the probability of occurrence of heads and tails.

Solution: The experimental probability for the occurrence of heads and tails in this experiment can be calculated as:

Experimental Probability of Occurrence of heads = Number of times head occurs/Number of times coin is tossed.

Experimental Probability of Occurrence of tails = Number of times tails occurs/Number of times coin is tossed.

We observe that if the number of tosses of the coin increases then the probability of occurrence of heads or tails also approaches to 0.5.

To know more about experimental probability and theoretical probability please download BYJU’S – The Learning App.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Math tutors
• Math classes
• 1st Grade Math Worksheets
• 2nd Grade Math Worksheets
• 3rd Grade Math Worksheets
• 4th Grade Math Worksheets
• 5th Grade Math Worksheets
• 6th Grade Math Worksheets
• 7th Grade Math Worksheets
• 8th Grade Math Worksheets
• Knowledge Base

Experimental Probability – Formula, Definition With Examples

Updated on January 12, 2024

Welcome to another exciting journey with us at Brighterly , where we make the learning of complex mathematical concepts a fun and engaging process. Today, we embark on a venture into the world of experimental probability, a vital aspect of mathematics that breathes life into numbers through practical, real-world experiences. But what exactly is experimental probability, and how does it differ from theoretical probability? How can we calculate experimental probability, and how is it applicable in our everyday lives? This article aims to answer these questions and more, unraveling the mysteries of experimental probability in an easy-to-understand and approachable manner.

Our trip into the world of experimental probability will cover the core concepts, definitions, and the all-important formula that underpins this fascinating area of mathematics. We’ll take a step back to appreciate the broader context of probability before focusing our lens on experimental probability, understanding its properties and contrasts with theoretical probability. With plenty of examples and practice problems, you’ll have a firm grasp on experimental probability, ready to see and use it in the world around you!

What Is Experimental Probability?

Probability, as a field of mathematics, often focuses on predicting the likelihood of certain events. However, it’s important to note that there are two main types of probability: theoretical and experimental. In this article, we will zero in on experimental probability.

Experimental probability, also known as empirical probability, is all about actual experiments and real-world observations. The main idea behind experimental probability is that it calculates the chances of an event happening based on the actual results of an experiment. This method of calculation is particularly interesting because it revolves around practical events that have already occurred, rather than theoretical or hypothetical situations.

In experimental probability, we conduct a certain experiment multiple times and observe the number of times a specific event occurs. This might sound quite complex, but we’ll dive into this concept with a greater depth in the upcoming sections, making it easily understandable.

Definition of Probability

Before we delve into experimental probability, let’s take a step back and understand the basic concept of probability. Probability is defined as a branch of mathematics that measures the likelihood of events to occur. It’s expressed as a number between 0 and 1, where 0 indicates impossibility and 1 signifies certainty.

For example, consider flipping a fair coin. The probability of landing a “heads” is 1 out of 2, or 0.5, meaning there’s a 50% chance to get a “heads”. The same applies to “tails”.

Understanding probability can help us make predictions about the outcomes of a random event and aids in making informed decisions in various aspects of life including gaming, statistics, and even weather forecasting.

Definition of Experimental Probability

Moving on to experimental probability, it is defined as the ratio of the number of times an event occurs to the total number of trials or times the activity is performed. The experimental probability of an event is calculated by conducting an experiment and recording the results.

For instance, let’s say we roll a dice 100 times, and the number “4” comes up 15 times. Here, the experimental probability of rolling a “4” would be the number of successful outcomes (rolling a “4”) divided by the total number of outcomes (total dice rolls), or 15/100 = 0.15.

In other words, experimental probability is the actual probability obtained from the direct observation or testing during an experiment. Unlike theoretical probability, it doesn’t rely on the inherent nature of the experiment, but rather on the actual data collected.

Properties of Probability

Understanding the properties of probability can provide us with insights about how probability functions. Here are some of the essential properties:

• The probability of an event ranges from 0 to 1.
• The sum of probabilities of all possible outcomes is always 1.
• The probability of the complement of an event (an event not happening) is 1 minus the probability of the event.
• If two events are mutually exclusive (they can’t occur at the same time), the probability of either event occurring is the sum of their individual probabilities.

These properties provide a foundational understanding of how probability works, whether it’s theoretical or experimental probability.

Properties of Experimental Probability

The properties of experimental probability are closely tied to those of theoretical probability, but with an emphasis on the data collected through experimentation. Here are the primary properties:

• Experimental probability also ranges from 0 to 1. An experimental probability of 0 means the event never happened in the experiment, and a probability of 1 means the event always occurred.
• As more trials are conducted, the experimental probability tends to approach the theoretical probability, given that the experiment is unbiased. This is known as the law of large numbers.
• Like in theoretical probability, the sum of experimental probabilities of all possible outcomes is 1.

Understanding these properties can greatly aid in interpreting the results of experiments and the likelihood of outcomes.

Difference Between Theoretical and Experimental Probability

The primary difference between theoretical and experimental probability lies in their calculation and interpretation. Theoretical probability is based on the possible outcomes in theory. It assumes that all outcomes are equally likely, which isn’t always the case in real-world scenarios.

On the other hand, experimental probability is based on actual data collected from performed experiments. It deals with the frequency of occurrence of an event, providing a more empirical perspective on probability. For example, in theory, the probability of rolling a “6” on a fair die is 1/6. However, in an actual experiment of, say, 60 rolls, we might roll a “6” only 8 times. The experimental probability then becomes 8/60 or 0.1333.

Formula of Experimental Probability

The formula of experimental probability is quite straightforward:

By using this formula, we can calculate the experimental probability of an event based on the results of an actual experiment or observation.

Understanding the Formula of Experimental Probability

To understand the formula of experimental probability, let’s revisit the dice rolling example. If you roll a die 100 times, and the number “4” comes up 20 times, then the experimental probability of rolling a “4” is:

Experimental Probability = Number of times event occurs / Total number of trials

Experimental Probability = 20 / 100 = 0.2

Hence, based on the results of this experiment, the experimental probability of rolling a “4” is 0.2 or 20%.

This formula essentially calculates the frequency of occurrence of an event in an experiment, providing a realistic interpretation of probability.

Calculating Experimental Probability Using the Formula

Let’s consider another example to illustrate the calculation of experimental probability using the formula. Imagine you’re shooting basketball hoops. You take 30 shots and make 18 of them. What’s the experimental probability of making a shot?

Applying the formula, we get:

Experimental Probability = 18 / 30 = 0.6

So, the experimental probability of making a shot, based on this experiment, is 0.6 or 60%.

Practice Problems on Experimental Probability

To better understand how to calculate experimental probability, let’s work through some practice problems:

• A spinner with 8 equal sections numbered 1 to 8 is spun 50 times. The number 3 comes up 7 times. What is the experimental probability of the spinner landing on 3?
• In a school, a survey of what pet each student has at home is conducted. Out of 200 students, 45 have dogs. What is the experimental probability that a randomly selected student has a dog?
• In a bag of 100 marbles, 25 are red, and the rest are blue. If you randomly select a marble, replace it, and repeat this 100 times, and you get a red marble 28 times, what is the experimental probability of drawing a red marble?
• Experimental Probability = 7 / 50 = 0.14
• Experimental Probability = 45 / 200 = 0.225
• Experimental Probability = 28 / 100 = 0.28

And that wraps up our enlightening exploration of experimental probability! With Brighterly, we’ve unpacked this fascinating mathematical concept, revealing its significance and wide-ranging applications in our everyday life. Experimental probability, with its basis in real-world observations, lends us the power to anticipate outcomes based on our experiences, paving the way for more informed decision-making.

From understanding the basic definition of probability to distinguishing between theoretical and experimental probability and mastering the formula of experimental probability, we hope you’re now well-equipped to navigate the captivating world of probability. Remember, probability isn’t just a concept confined within the pages of a mathematics textbook; it’s very much a part of the world around us, informing everything from weather forecasts to game strategy and risk analysis.

So, the next time you play a game of cards, shoot hoops, or even make a decision based on certain outcomes, remember the role of experimental probability! As always, the team at Brighterly is dedicated to making the learning of complex concepts enjoyable, ensuring you have fun on your journey of exploration. Stay tuned for more exciting math adventures!

Frequently Asked Questions on Experimental Probability

What is experimental probability.

Experimental probability is a probability value that is based on actual experiments or observations. In other words, it’s a type of probability that quantifies the ratio of the number of times an event occurs to the total number of trials or times an activity is performed. For example, if you flip a coin 100 times and it lands on heads 45 times, the experimental probability of getting heads is 45/100 = 0.45 or 45%.

How do you calculate experimental probability?

Calculating experimental probability is straightforward. It involves dividing the number of times an event occurs by the total number of trials. For instance, if you roll a die 60 times and get a ‘6’ on 10 occasions, the experimental probability of rolling a ‘6’ would be 10 (number of successful outcomes) divided by 60 (total number of outcomes), which equals 0.1667 or 16.67%.

What is the difference between theoretical and experimental probability?

Theoretical probability and experimental probability differ in their calculation and interpretation. Theoretical probability is a type of probability that assumes that all outcomes of an experiment are equally likely. It’s calculated by dividing the number of favorable outcomes by the total number of possible outcomes.

On the other hand, experimental probability doesn’t rely on the assumption of equally likely outcomes but instead depends on actual data collected from conducted experiments. It deals with the frequency or proportion of times an event occurs based on experimental data.

Why is experimental probability important?

Experimental probability plays a crucial role in various fields and everyday life. Its importance lies in its basis on real-world data, which makes it a practical tool for predicting the likelihood of outcomes based on past experiences. Experimental probability is utilized in various sectors such as statistics, data analysis, gaming, weather forecasting, and in the medical field, among others. It also plays a key role in empirical research, where it aids in providing evidence-based conclusions.

• Wikipedia – Probability
• NCBI – Probability in Health
• Gov.uk – Understanding Uncertainty and Risk

As a seasoned educator with a Bachelor’s in Secondary Education and over three years of experience, I specialize in making mathematics accessible to students of all backgrounds through Brighterly. My expertise extends beyond teaching; I blog about innovative educational strategies and have a keen interest in child psychology and curriculum development. My approach is shaped by a belief in practical, real-life application of math, making learning both impactful and enjoyable.

Math homework help for grade 1-8

Get the homework support your child needs!

Choose kid's grade

Math Program Boost Your Child's Math Abilities! Ideal for 1st-8th Graders, Perfectly Synced with School Curriculum!

After-school math classes for grades 1-8

Personalized lessons for kids & teens.

Our after-school math curriculum includes

Related math, 16 times table – multiplication table.

Multiplication Table of 16 Learning the 16 times table is a vital step in mastering mathematics, especially for children in middle school. By knowing the multiplication table of 16, students can quickly solve problems and understand more complex mathematical concepts. The 16 times table is simply a set of mathematical results you get when you […]

Hexadecimal to Decimal Conversion: Steps, Chart, and Examples

Hexadecimal and decimal are some of the different types of number systems. There are other types; octal and binary number systems. These systems were designed to help us organize and represent numbers in maths, finance, engineering, and science. In this article, we discuss what the hexadecimal system is, convert hexadecimal to decimal number systems with […]

230000 in Words

We write 230000 in words as “two hundred thirty thousand”. This number is two hundred thirty sets of one thousand each. If a city has two hundred thirty thousand residents, it means it has two hundred thirty thousand residents in total. Thousands Hundreds Tens Ones 230 0 0 0 How to Write 230000 in Words? […]

Want your kid to excel in math?

Kid’s grade

Close a child’s math gaps with a tutor!

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More