word problem solving involving quadratic equation

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Rectangular Prism
• Fibonacci Sequence
• Golden Ratio
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation
• Triangular Number
• Complex Number
• Binary Number System
• Binomial Theorem
• Quartic Function
• Mathematical Induction
• Group Theory
• Modular Arithmetic
• Euler’s Number
• Inequalities
• De Morgan’s Laws
• Transcendental Numbers

Last modified on August 3rd, 2023

Quadratic Equation Word Problems

Here, we will solve different types of quadratic equation-based word problems. Use the appropriate method to solve them:

• By Completing the Square
• By Factoring
• By Quadratic Formula
• By graphing

For each process, follow the following typical steps:

• Make the equation
• Solve for the unknown variable using the appropriate method
• Interpret the result

The product of two consecutive integers is 462. Find the numbers?

Let the numbers be x and x + 1 According to the problem, x(x + 1) = 483 => x 2 + x – 483 = 0 => x 2 + 22x – 21x – 483 = 0 => x(x + 22) – 21(x + 22) = 0 => (x + 22)(x – 21) = 0 => x + 22 = 0 or x – 21 = 0 => x = {-22, 21} Thus, the two consecutive numbers are 21 and 22.

The product of two consecutive positive odd integers is 1 less than four times their sum. What are the two positive integers.

Let the numbers be n and n + 2 According to the problem, => n(n + 2) = 4[n + (n + 2)] – 1 => n 2 + 2n = 4[2n + 2] – 1 => n 2 + 2n = 8n + 7 => n 2 – 6n – 7 = 0 => n 2 -7n + n – 7 = 0 => n(n – 7) + 1(n – 7) = 0 => (n – 7) (n – 1) = 0 => n – 7 = 0 or n – 1 = 0 => n = {7, 1} If n = 7, then n + 2 = 9 If n = 1, then n + 1 = 2 Since 1 and 2 are not possible. The two numbers are 7 and 9

A projectile is launched vertically upwards with an initial velocity of 64 ft/s from a height of 96 feet tower. If height after t seconds is reprented by h(t) = -16t 2 + 64t + 96. Find the maximum height the projectile reaches. Also, find the time it takes to reach the highest point.

Since the graph of the given function is a parabola, it opens downward because the leading coefficient is negative. Thus, to get the maximum height, we have to find the vertex of this parabola. Given the function is in the standard form h(t) = a 2 x + bx + c, the formula to calculate the vertex is: Vertex (h, k) = ${\left\{ \left( \dfrac{-b}{2a}\right) ,h\left( -\dfrac{b}{2a}\right) \right\}}$ => ${\dfrac{-b}{2a}=\dfrac{-64}{2\times \left( -16\right) }}$ = 2 seconds Thus, the time the projectile takes to reach the highest point is 2 seconds ${h\left( \dfrac{-b}{2a}\right)}$ = h(2) = -16(2) 2 – 64(2) + 80 = 144 feet Thus, the maximum height the projectile reaches is 144 feet

The difference between the squares of two consecutive even integers is 68. Find the numbers.

Let the numbers be x and x + 2 According to the problem, (x + 2) 2 – x 2 = 68 => x 2 + 4x + 4 – x 2 = 68 => 4x + 4 = 68 => 4x = 68 – 4 => 4x = 64 => x = 16 Thus the two numbers are 16 and 18

The length of a rectangle is 5 units more than twice the number. The width is 4 unit less than the same number. Given the area of the rectangle is 15 sq. units, find the length and breadth of the rectangle.

Let the number be x Thus, Length = 2x + 5 Breadth = x – 4 According to the problem, (2x + 5)(x – 4) = 15 => 2x 2 – 8x + 5x – 20 – 15 = 0 => 2x 2 – 3x – 35 = 0 => 2x 2 – 10x + 7x – 35 = 0 => 2x(x – 5) + 7(x – 5) = 0 => (x – 5)(2x + 7) = 0 => x – 5 = 0 or 2x + 7 = 0 => x = {5, -7/2} Since we cannot have a negative measurement in mensuration, the number is 5 inches. Now, Length = 2x + 5 = 2(5) + 5 = 15 inches Breadth = x – 4 = 15 – 4 = 11 inches

A rectangular garden is 50 cm long and 34 cm wide, surrounded by a uniform boundary. Find the width of the boundary if the total area is 540 cm².

Given, Length of the garden = 50 cm Width of the garden = 34 cm Let the uniform width of the boundary be = x cm According to the problem, (50 + 2x)(34 + 2x) – 50 × 34 = 540 => 4x 2 + 168x – 540 = 0 => x 2 + 42x – 135 = 0 Since, this quadratic equation is in the standard form ax 2 + bx + c, we will use the quadratic formula, here a = 1, b = 42, c = -135 x = ${x=\dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}}$ => ${\dfrac{-42\pm \sqrt{\left( 42\right) ^{2}-4\times 1\times \left( -135\right) }}{2\times 1}}$ => ${\dfrac{-42\pm \sqrt{1764+540}}{2}}$ => ${\dfrac{-42\pm \sqrt{2304}}{2}}$ => ${\dfrac{-42\pm 48}{2}}$ => ${\dfrac{-42+48}{2}}$ and ${\dfrac{-42-48}{2}}$ => x = {-45, 3} Since we cannot have a negative measurement in mensuration the width of the boundary is 3 cm

The hypotenuse of a right-angled triangle is 20 cm. The difference between its other two sides is 4 cm. Find the length of the sides.

Let the length of the other two sides be x and x + 4 According to the problem, (x + 4) 2 + x 2 = 20 2 => x 2 + 8x + 16 + x 2 = 400 => 2x 2 + 8x + 16 = 400 => 2x 2 + 8x – 384 = 0 => x 2 + 4x – 192 = 0 => x 2 + 16x – 12x – 192 = 0 => x(x + 16) – 12(x + 16) = 0 => (x + 16)(x – 12) = 0 => x + 16 = 0 and x – 12 = 0 => x = {-16, 12} Since we cannot have a negative measurement in mensuration, the lengths of the sides are 12 and 16

Jennifer jumped off a cliff into the swimming pool. The function h can express her height as a function of time (t) = -16t 2 +16t + 480, where t is the time in seconds and h is the height in feet. a) How long did it take for Jennifer to attain a maximum length. b) What was the highest point that Jennifer reached. c) Calculate the time when Jennifer hit the water?

Comparing the given function with the given function f(x) = ax 2 + bx + c, here a = -16, b = 16, c = 480 a) Finding the vertex will give us the time taken by Jennifer to reach her maximum height  x = ${-\dfrac{b}{2a}}$ = ${\dfrac{-16}{2\left( -16\right) }}$ = 0.5 seconds Thus Jennifer took 0.5 seconds to reach her maximum height b) Putting the value of the vertex by substitution in the function, we get ${h\left( \dfrac{1}{2}\right) =-16\left( \dfrac{1}{2}\right) ^{2}+16\left( \dfrac{1}{2}\right) +480}$ => ${-16\left( \dfrac{1}{4}\right) +8+480}$ => 484 feet Thus the highest point that Jennifer reached was 484 feet c) When Jennifer hit the water, her height was 0 Thus, by substituting the value of the height in the function, we get -16t 2 +16t + 480 = 0 => -16(t 2 + t – 30) = 0 => t 2 + t – 30 = 0 => t 2 + 6t – 5t – 30 = 0 => t(t + 6) – 5(t + 6) = 0 => (t + 6)(t – 5) = 0 => t + 6 = 0 or t – 5 = 0 => x = {-6, 5} Since time cannot have any negative value, the time taken by Jennifer to hit the water is 5 seconds.

Leave a comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

Need Help Solving Those Dreaded Word Problems Involving Quadratic Equations?

Yes, I know it's tough. You've finally mastered factoring and using the quadratic formula and now you are asked to solve more problems!

Except these are even more tough. Now you have to figure out what the problem even means before trying to solve it. I completely understand and here's where I am going to try to help!

There are many types of problems that can easily be solved using your knowledge of quadratic equations. You may come across problems that deal with money and predicted incomes (financial) or problems that deal with physics such as projectiles. You may also come across construction type problems that deal with area or geometry problems that deal with right triangles.

Lucky for you, you can solve the quadratic equations, now you just have to learn how to apply this useful skill.

On this particular page, we are going to take a look at a physics "projectile problem".

Projectiles - Example 1

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. Find the maximum height attained by the ball.

Let's first take a minute to understand this problem and what it means. We know that a ball is being shot from a cannon. So, in your mind, imagine a cannon firing a ball. We know that the ball is going to shoot from the cannon, go into the air, and then fall to the ground.

So, here's a mathematical picture that I see in my head.

Now let's talk about what each part of this problem means. In our equation that we are given we must be given the value for the force of gravity (coefficient of t 2 ). We must also use our upward velocity (coefficient of t) and our original height of the cannon/ball (the constant or 1.5). Take a look...

Now that you have a mental picture of what's happening and you understand the formula given, we can go ahead and solve the problem.

• First, ask yourself, "What am I solving for?" "What do I need to find?" You are asked to find the maximum height (go back and take a look at the diagram). What part of the parabola is this? Yes, it's the vertex! We will need to use the vertex formula and I will need to know the y coordinate of the vertex because it's asking for the height.
• Next Step: Solve! Now that I know that I need to use the vertex formula, I can get to work.

Just as simple as that, this problem is solved.

Let's not stop here. Let's take this same problem and put a twist on it. There are many other things that we could find out about this ball!

Projectiles - Example 2

Same problem - different question. Take a look...

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long did it take for the ball to reach the ground?

Now, we've changed the question and we want to know how long did it take the ball to reach the ground.

What ground, you may ask. The problem didn't mention anything about a ground. Let's take a look at the picture "in our mind" again.

Do you see where the ball must fall to the ground. The x-axis is our "ground" in this problem. What do we know about points on the x-axis when we are dealing with quadratic equations and parabolas?

Yes, the points on the x-axis are our "zeros" or x-intercepts. This means that we must solve the quadratic equation in order to find the x-intercept.

Let's do it! Let's solve this equation. I'm thinking that this may not be a factorable equation. Do you agree? So, what's our solution?

Hopefully, you agree that we can use the quadratic formula to solve this equation.

The first time doesn't make sense because it's negative. This is the calculation for when the ball was on the ground initially before it was shot.

This actually never really occurred because the ball was shot from the cannon and was never shot from the ground. Therefore, we will disregard this answer.

The other answer was 2.54 seconds which is when the ball reached the ground (x-axis) after it was shot. Therefore, this is the only correct answer to this problem.

Ok, one more spin on this problem. What would you do in this case?

Projectiles - Example 3

A ball is shot from a cannon into the air with an upward velocity of 40 ft/sec. The equation that gives the height (h) of the ball at any time (t) is: h(t)= -16t 2 + 40ft + 1.5. How long does it take the ball to reach a height of 20 feet?

Yes, this problem is a little trickier because the question is not asking for the maximum height (vertex) or the time it takes to reach the ground (zeros), instead it it asking for the time it takes to reach a height of 20 feet.

Since the ball reaches a maximum height of 26.5 ft, we know that it will reach a height of 20 feet on the way up and on the way down.

Let's just estimate on our graph and also make sure that we get this visual in our head.

From looking at this graph, I would estimate the times to be about 0.7 sec and 1.9 sec. Do you see how the ball will reach 20 feet on the way up and on the way down?

Now, let's find the actual values. Where will we substitute 20 feet?

Yes, we must substitute 20 feet for h(t) because this is the given height. We will now be solving for t using the quadratic formula. Take a look.

Our actual times were pretty close to our estimates. Just don't forget that when you solve a quadratic equation, you must have the equation set equal to 0. Therefore, we had to subtract 20 from both sides in order to have the equation set to 0.

You've now seen it all when it comes to projectiles!

Great Job! Hopefully you've been able to understand how to solve problems involving quadratic equations. I also hope that you better understand these common velocity equations and how to think about what this problem looks like graphically in order to help you to understand which process or formula to use in order to solve the problem.

• Quadratic Equations
• Projectile Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

• The Basic math blog
• Member Login
• Pre-Algebra Lessons
• Pre-Algebra Word Problems
• Pre-Algebra Calculators
• Algebra Lessons
• Algebra Word Problems
• Algebra Proofs
• Advanced Algebra
• Algebra Calculators
• Geometry Lessons
• Geometry Word Problems
• Geometry Proofs
• Geometry Calculators
• Trigonometry Lessons
• Numeration System
• Basic Concepts of Set Theory
• Consumer Math
• Baseball Math
• Math for Nurses
• Statistics Made Easy
• High School Physics
• Basic Mathematics Store
• Math Vocabulary Quizzes
• SAT Math Prep
• Math Skills by Grade Level
• Ask an Expert
• Other Websites
• K-12 Worksheets
• Worksheets Generator
• Algebra Worksheets
• Geometry Worksheets
• Fun Online Math Games
• Pre-Algebra Games
• Math Puzzles
• Math Tricks

Word problems involving quadratic equations

Check out these four great word problems involving quadratic equations in this lesson. 

Problem #1: A rectangular garden has an area of 14 m 2 and a perimeter of 18 meters. Find the dimensions of the rectangular garden. The figure below shows how to set up the problem.

Let w = width and l = length

2l + 2w = 18

Divide both sides of 2l + 2w = 18 by 2 to get l + w = 9.

Using l + w = 9, solve for l. We get l = 9 - w.

Substitute 9 - w for l in lw = 14 ( 9 - w)w = 14   9w - w 2 = 14 9w - w 2  - 14 = 0 - w 2  + 9w - 14 = 0 w 2  - 9w + 14 = 0

(w - 7)(w - 2) = 0

w = 7 and w  = 2

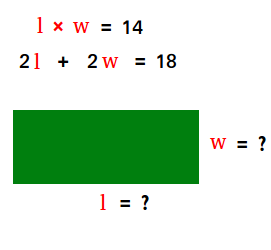
Problem #2: The sum of two numbers is 12 and their product is 35. What are the two numbers?

Solution: 

Let n and m be the two numbers.

n + m = 12  (1) n × m = 35  (2)

Using (1), n = 12 - m

(12 - m) × m = 35

Interesting word problems involving quadratic equations.

Problem #3: The quadratic equation for the cost in dollars of producing automobile tires is given below where x is the number of tires the company produces. Find the number of tires that will minimize the cost.

Solution:  The standard form of a quadratic equation is ax² + bx + c. To solve this problem, we just need 2 important concepts about quadratic equations. First, when we are trying to maximize or minimize, we need to use the formula below that will help us find the x-coordinate of the vertex. Second, if a > 0, the vertex is a minimum.  if a < 0, the vertex is a maximum.

Since a = 0.00002 and 0.00002 is bigger than 0, the quadratic equation will give a minimum.

Problem #4: You want to frame a collage of pictures with a 9-ft strip of wood. What dimensions will help you maximize the area? Solution:  First, we need to find the quadratic equation.  Area = l × w                                   Perimeter = 2l + 2w 9 = 2l + 2w. Solve for l and replace l in the formula for the area.

9 - 2w = 2l

A = -w 2 + 4.5w

A = -w 2  + 4.5w + 0

Since a = -1 and -1 is smaller than 0, the quadratic equation will give a maximum. 

If you found the word problems involving quadratic equations on this lesson difficult to understand, review the lesson about  factoring trinomials

Special Math Topics

Applied math.

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

QUADRATIC EQUATION WORD PROBLEMS WORKSHEET WITH ANSWERS

Problem 1 :

Difference between a number and its positive square root is 12. Find the number.

Problem 2 :

If the difference between a number and its reciprocal is ²⁴⁄₅ , find the number.

Problem 3 :

A piece of iron rod costs $60. If the rod was 2 meter shorter and each meter costs $1 more, the cost would remain unchanged. What is the length of the rod?

Problem 4 :

Divide 25 in two parts so that sum of their reciprocals is ⅙ .

Problem 5 :

The hypotenuse of a right angled triangle is 20 cm. The difference between its other two sides is 4 cm. Find the length of the sides.

Problem 6 :

The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.

Problem 7 :

A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article(in dollars) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was $90, find the number of articles produced and the cost of each article.

Problem 8 : 

The sides of an equilateral triangle are shortened by 12 units, 13 units and 14 units respectively and a right angle triangle is formed. Find the length of each side of the equilateral triangle.

1. Answer :

Let x be the required number.

Its positive square root is √x.  

Given : Difference between x and √x is 12.

x - √x = 12

x - 12 = √x

(x - 12) 2  = x

x 2 - 24x + 144 = x

Subtract x from both sides.

x 2  - 25x + 144 = 0

x 2  - 9x - 16x + 144 = 0

x(x - 9) - 16(x - 9) = 0

(x - 9)(x - 16) = 0

x = 9  or  x = 16

x = 9 does not satisfy the condition given in the question.

Then, 

x  =  16

Therefore, the required number is 16.

2. Answer :

Let y be the required number.

Then, its reciprocal is ¹⁄ y .

Given : D ifference between a number and its reciprocal is ²⁴⁄₅ .

y - ¹⁄ y   =  ²⁴⁄₅

Multiply both sides by 5y to get rid of the denominators y and 5.

5y(y  - ¹⁄ y ) = 5y( ²⁴⁄₅ )

5y(y) - 5y( ¹⁄ y ) = 24y 

5y 2 - 5 = 24y

Subtract 24y from boths sides.

5y 2 - 24y - 5 = 0

Solve by factoring.

5y 2 - 25y + y - 5 = 0

5y(y - 5) + 1(y - 5) = 0

(y - 5)(5y + 1) = 0

y - 5 = 0  or  5y + 1 = 0

y = 5  or  y =  ⁻¹⁄₅

Justification :

Both the values y =  5  and y =  ⁻¹⁄₅  satisfy the condition given in the question.

Therefore, the required number is 5 or  ⁻¹⁄₅ .

3. Answer :

Let x be the length of the given rod. Then the length of the rod 2 meter shorter is (x - 2) and the total cost of both the rods is $60 (Because cost would remain unchanged).  Cost of one meter of the given rod  is

=  ⁶⁰⁄ₓ 

Cost of one meter of the rod which is 2 meter shorter is

=  ⁶⁰⁄₍ₓ ₋ ₂₎

Given :  If the rod was 2 meter shorter and each meter costs $1 more.

That is,  60/(x-2) is $1 more than 60/x.

⁶⁰⁄₍ₓ ₋ ₂₎  -  ⁶⁰⁄ₓ  = 1

Multiply both sides by x(x - 2) to get rid of the denominators (x - 2) an x.

x(x - 2) [⁶⁰⁄₍ₓ ₋ ₂₎  -  ⁶⁰⁄ₓ]  = x(x - 2)

x(x - 2) [⁶⁰⁄₍ₓ ₋ ₂₎]  - x(x - 2) [⁶⁰⁄ₓ]  = x(x - 2)

60x - 60(x - 2) = x 2  - 2x

60x - 60x + 120 = x 2  - 2x

120 = x 2  - 2x

0 = x 2  - 2x - 120 

x 2  - 2x - 120 = 0

x 2  - 12x + 10x - 120 = 0

x(x - 12) + 10(x - 12) = 0

(x - 12)(x + 10) = 0

x - 12 = 0  or  x + 10 = 0

x = 12  or  x = -10

Because length can not be a negative number, we can ignore x = -10. 

Therefore, the length of the given rod is 12 m.

4. Answer :

Let x be one of the parts of 25.

Then, the other part is (25 - x).  Given : Sum of the reciprocals of the parts is 1/6. 

¹⁄ₓ  +  ¹⁄₍₂₅ ₋ ₓ₎ =  ⅙

Multiply both sides by 6x(25 - x) to get rid of the denominators x, (25 - x) and 6.

6x(25 - x) [ ¹⁄ₓ  +  ¹⁄₍₂₅ ₋ ₓ₎ ]  = 6x(25 - x) [⅙]

6x(25 - x) [ ¹⁄ₓ ]  - 6x(25 - x) [ ¹⁄₍₂₅ ₋ ₓ₎ ]  = x(25 - x)

6(25 - x) - 6x = 25x - x 2

150 - 6x + 6x = 25x - x 2

150 = 25x -  x 2

x 2  - 2 5x + 150 = 0

x 2  - 1 5x - 10x + 150 = 0

x(x - 15) - 10(x - 15) = 0

(x - 15)(x - 10) = 0

x - 15 = 0  or x - 10 = 0

x = 15  or  x = 10

When x = 15, 

25 - x = 25 - 15

When x = 10,

25 - x = 25 - 10

Therefore, the two parts of 25 are 10 and 15.

5. Answer :

From the given information. we can assume x and ( x + 4) as the lengths of the other two sides of the right triangle.

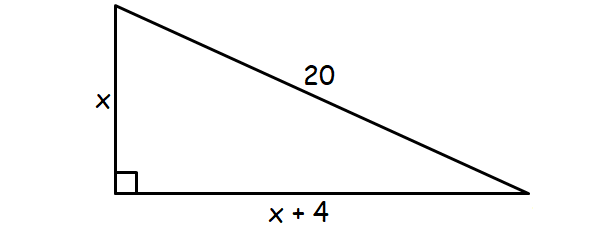
Using Pythagorean Theorem in the right triangle above,

x 2  + (x + 4) 2  = 20 2

x 2  + (x + 4)(x + 4) = 400

x 2  + x 2  + 4x + 4x + 16 = 400

2x 2  + 8x + 16 = 400

2 x 2  + 8x - 384 = 0

Divide both sides by 2. 

x 2  + 4x - 192 = 0

x 2  - 12x + 16x - 192 = 0

x(x - 12) + 16(x - 12) = 0

(x - 12)(x + 16) = 0

x - 12 = 0  or  x + 16 = 0

x = 12  or  x = -16

x = -16 can not be accepted. Because length can never be negative.

Therefore, the other two sides of the triangle are 12 cm and 16 cm.

6. Answer :

Let x be the base the right triangle.

Then, its altitude is ( x - 7).

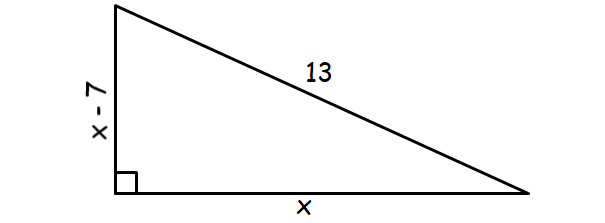
x 2 + (x - 7) 2 = 13 2

x 2 + (x - 7)(x - 7) = 169

x 2  + x 2  - 7x - 7x + 49  = 169

2x 2  - 14x + 49 = 169

2x 2  - 14x - 120 = 0

Divide both sides by 2.

x 2  - 7x - 60 = 0

x 2  - 12x + 5x - 60 = 0

x(x - 12) + 5(x - 12) = 0

(x + 5)(x - 12) = 0

x + 5 = 0  or  x - 12 = 0

x = -5  or  x = 12

Because x represents the base of the triangle, it can never be negative. So, x = 12 

Base = 12 cm

 Altitude = 5 cm

Therefore, the other two sides of the right triangle are 12 cm and 5 cm.

7. Answer :

Let x be the number of articles produced on that day.

Then, the cost of production of each article is

Total cost = N umber of articles  ⋅ cost of one article

90 = x(2x + 3)

90 = 2x 2  + 3x

2x 2  + 3x - 90 = 0

Solv by factoring.

2x 2  - 12x + 15 x - 90 = 0

2x(x - 6) + 15(x - 6) = 0

(2x + 15)(x - 6) = 0

2x + 15 = 0  or  x - 6 = 0

x = -7.5  or  x = 6

Because x represents the number of articles, it can never be negative value. Then,  x = 6.

So, the number of articles produced is 6.

The cost of each article : 

8. Answer :

Let x be the length of each side of the equilateral triangle.

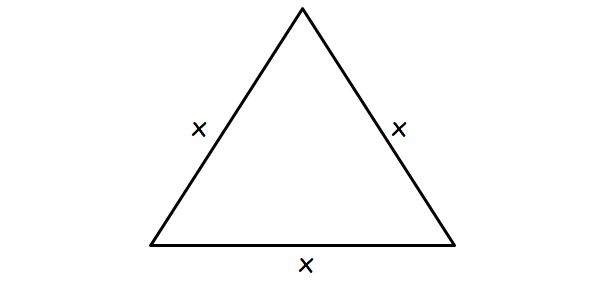
Then, the sides of the right angle triangle are

(x - 12), (x - 13) and (x - 14) 

In the above three sides, the side represented by ( x - 12) is hypotenuse (because, that is the longest side).

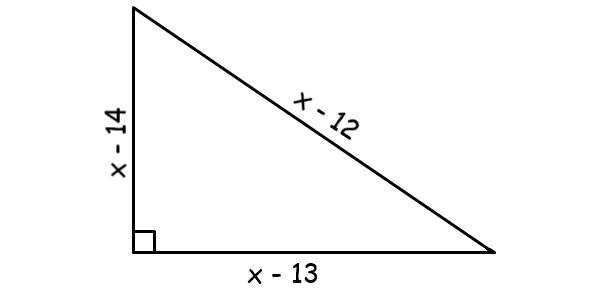
(x - 13) 2  + (x - 14) 2  = (x - 12) 2

(x - 13)(x - 13) + (x - 14)(x - 14)   = (x - 12)(x - 12)

x 2  - 26x + 169 + x 2  - 28x + 196 =  x 2  - 24x + 144

2x 2  - 54x + 365 = x 2  - 24x + 144

x 2  - 30x + 221 = 0

x 2  - 13x - 17x + 221 = 0

x(x - 13) - 17(x - 13) = 0

(x - 13)(x - 17) = 0

x - 13 = 0  or  x - 17 = 0

x = 13  or  x = 17 

x = 13 can not be accepted.

Because, if x = 13, the side represented by ( x - 14) is negative. So, x = 17. Therefore, the length of each side of the equilateral triangle is 17 units.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Nov 21, 24 06:23 AM

Digital SAT Math Problems and Solutions (Part - 75)

Nov 21, 24 06:13 AM

Digital SAT Math Problems and Solutions (Part - 74)

Nov 20, 24 08:12 AM

• Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
• Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
• Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
• Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
• Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Testing Solutions Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Quadrant Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Equation Given Points
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Testing Solutions
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Number Line

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic - solving...

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

Quadratic Equations Word Problems

These lessons, with videos, examples, and step-by-step solutions, help Algebra 1 students learn to solve geometry word problems using quadratic equations.

Related Pages Solving Quadratic Equations by Factoring Solving Quadratic Equations by Completing the Square More Lessons for Grade 9 Math Worksheets

Quadratic equations - Solving word problems using factoring of trinomials Question 1a: Find two consecutive integers that have a product of 42

Quadratic equations - Solving word problems using factoring of trinomials Question 1b: There are three consecutive integers. The product of the two larger integers is 30. Find the three integers.

Quadratic Equations - Solving Word problems by Factoring Question 1c: A rectangular building is to be placed on a lot that measures 30 m by 40 m. The building must be placed in the lot so that the width of the lawn is the same on all four sides of the building. Local restrictions state that the building cannot occupy any more than 50% of the property. What are the dimensions of the largest building that can be built on the property?

More Word Problems Using Quadratic Equations Example 1 Suppose the area of a rectangle is 114.4 m 2 and the length is 14 m longer than the width. Find the length and width of the rectangle.

More Word Problems Using Quadratic Equations Example 2 A manufacturer develops a formula to determine the demand for its product depending on the price in dollars. The formula is D = 2,000 + 100P - 6P 2 where P is the price per unit, and D is the number of units in demand. At what price will the demand drop to 1000 units?

More Word Problems Using Quadratic Equations Example 3 The length of a car’s skid mark in feet as a function of the car’s speed in miles per hour is given by l(s) = .046s 2 - .199s + 0.264 If the length of skid mark is 220 ft, find the speed in miles per hour the car was traveling.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Quadradic Equation Word Problems - Examples & Practice - Expii

Quadradic equation word problems - examples & practice, explanations (3), quadratic word problems.

Let's look at 2 pretty common types of word problems that use quadratic functions. Recall that quadratic expressions follow this general form: y=ax2+bx+c In a quadratic expression, a and b are coefficients (numbers in front of the variable x), and c is constant (a number by itself). It's important to remember that a≠0 . It's possible for b=0 and/or c=0, but they don't have to.

Example 1: Word problems involving area

Many quadratic word problems use the area of a rectangle. Here is a graphic to get you started

Image source: By Caroline Kulczycky

Here is another example.

Singh knows the total area of his garden is 50 m2, but he doesn't know the length or width. Use the diagram below to find the length and width in meters (m).

Recall that the formula for area of a rectangle is length⋅width. So, let's plug the values from Singh's garden into that formula, and set it equal to 50 (the area). area=length⋅width50=x⋅(x−5)

Now, let's multiply out this equation and get it in the standard quadratic form (written at the top of this explanation):

Once we multiply the equation out and rearrange it, what does it look like (in quadratic form)?

−x2−5x−50=0

−x2−5x+50=0

Related Lessons

(videos) solving geometry word problems using quadratic equations.

by PatrickJMT

This video by Patrick JMT covers a quadratic word problem based on area of a rectangle.

Patrick walks us through how to solve the following quadratic geometry problem:

“A picture inside a frame is 2 inches longer than it is wide. The picture is in a frame that has width 3 inches on each side of the picture. If the area of the pic, including the frame is 195 in.2, find the dimensions of the frame.”

He goes on to explain how we get the equations for the sides of the frame, so the whole problem looks like:

We know the area of the picture frame, 195 in2. We can set the two sides of the frame equal to that and find a value for x.

(x+6)(x+8)=195

Using the FOIL method , we get an equation that looks like

x2+14x+48=195

We want the left side to equal 0, so subtracting 195 from both sides will give us

x2+14x–147=0

This looks pretty hard to factor. Let’s use our handy dandy quadratic formula .

Our values are going to be a=1,b=14, and c=−147

x=−b±√b2−4ac2ax=−14±√142–4(1)(−147)2(1)x=−14±√196+5882x=−14±√7842x=−14±282x=−7±14

*Note: be careful with the square root!

This leaves us two values for x, x=7 or x=−21. We cannot have a negative measurement, so our final answer is x=7.

(Videos) Solve Projectile Problems Using Quadratics

This video by Patrick JMT works through a word problem based on projectile motion .

Solving a Projectile Problem Using Quadratics

Patrick uses the following problem as an example of projectile motion:

“Larry throws a rock in the air. The height, h, in feet above the ground of the rock is given by: h=−16t2+123t+40. How long is the rock in the air?”

From this equation, at time t=0, we gather that h=40. This means Larry is on a cliff with height 40. We want to know the time at which the rock reaches a height of 0. So, plugging in 0 for h, we get an equation:

0=−16t2+123t+40

This is now a quadratic equation, which we can solve for using the quadratic formula! We have values of a=16,b=123, and c=40. We can plug these into the quadratic formula: t=−b±√b2−4ac2at=−123±√(123)2−4(−16)(40)2(−16)t=−123±√17689−32t=123±√1768932t=123±13332t=8,−516

We get two solutions: 8 and −516. t is time, which can't be negative, so our answer is t=8.

Practice Problems

\(\textbf{1)}\) the length of a rectangle is 3 times its width. the area of the rectangle is 48 square yards. find the dimensions of the rectangle. show answer \( \text{width} = 4 \text{ yards}, \text{length} = 12 \text{ yards} \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=3w, \, a=48\) \(\,\,\,\,\, \left(3w\right)\left(w\right)=48\) \(\,\,\,\,\, 3w^2=48\) \(\,\,\,\,\, w^2=16\) \(\,\,\,\,\, w=\pm4\) \(\,\,\,\,\, w=4\) \(\,\,\,\,\, l=3(4)=12\) \(\,\,\,\,\, \text{width} = 4 \text{ yards}, \text{length} = 12 \text{ yards} \), \(\textbf{2)}\) the length of a rectangle is 4 times its width. the area of the rectangle is 100 square feet. find the dimensions of the rectangle. show answer \( \text{width} = 5 \text{ ft}, \text{length} = 20 \text{ ft} \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=4w, \, a=100\) \(\,\,\,\,\, \left(4w\right)\left(w\right)=100\) \(\,\,\,\,\, 4w^2=100\) \(\,\,\,\,\, w^2=25\) \(\,\,\,\,\, w=5\) \(\,\,\,\,\, l=4(w)=4(5)=20\) \(\,\,\,\,\, \text{width} = 5 \text{ ft}, \text{length} = 20 \text{ ft} \), \(\textbf{3)}\) the length of a rectangular plot is 5 ft more than its width. the area of the plot is 66 square ft. find the dimensions of the plot. show answer \( \text{width} = 6 \text{ ft}, \text{length} = 11 \text{ ft} \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=w+5, \, a=66\) \(\,\,\,\,\, (w+5)w=66\) \(\,\,\,\,\, w^2+5w-66=0\) \(\,\,\,\,\, (w+11)(w-6)=0\) \(\,\,\,\,\, w=-11 \text{ or } w=6\) \(\,\,\,\,\, l=6+5=11 \text{ or } l=-11+5=-6\) \(\,\,\,\,\, \text{width} = 6 \text{ ft}, \text{length} = 11 \text{ ft} \), \(\textbf{4)}\) the length of a rectangle is 15 feet less than its width. the area of the rectangle is 126 square feet. find the dimensions of the rectangle. show answer \( \text{width} = 6 \text{ ft}, \text{length} = 21 \text{ ft} \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=w-15, \, a=126\) \(\,\,\,\,\, (w-15)w=126\) \(\,\,\,\,\, w^2-15w-126=0\) \(\,\,\,\,\, (w-21)(w+6)=0\) \(\,\,\,\,\, w=21 \text{ or } w=-6\) \(\,\,\,\,\, l=21-15=6 \text{ or } l=-6-15=-21\) \(\,\,\,\,\, \text{width} = 21 \text{ ft}, \text{length} = 6 \text{ ft} \), \(\textbf{5)}\) the length of a rectangle is 3 inches more than double the width. the area of the rectangle is 230 square inches. find the dimensions of the rectangle. show answer \(\text{length} = 23 \text{ in}, \text{width} = 10 \text{ in} \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=2w+3, \, a=230\) \(\,\,\,\,\, (2w+3)w=230\) \(\,\,\,\,\, 2w^2+3w-230=0\) \(\,\,\,\,\, (2w+23)(w-10)=0\) \(\,\,\,\,\, w=-23/2 \text{ or } w=10\) \(\,\,\,\,\, l=2(10)+3=23 \text{ or } l=2(-23/2)+3=-23+3=-20\) \(\,\,\,\,\, \text{length} = 23 \text{ in}, \text{width} = 10 \text{ in} \), \(\textbf{6)}\) the length of a rectangle is 5 meters more than triple the width. the area is 138 square meters. find the dimensions of the rectangle. show answer \(\text{width} = 6 \text{ m}, \text{length} = 23 \text{ m}\) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l=3w+5, \, a=138\) \(\,\,\,\,\, (3w+5)w=138\) \(\,\,\,\,\, 3w^2+5w-138=0\) \(\,\,\,\,\, (3w+23)(w-6)=0\) \(\,\,\,\,\, w=-23/3 \text{ or } w=6\) \(\,\,\,\,\, l=3(6)+5=18+5=23 \text{ or } l=3(-23/3)+5=-23+5=-18\) \(\,\,\,\,\, \text{width} = 6 \text{ m}, \text{length} = 23 \text{ m}\), \(\textbf{7)}\) the width of a rectangle is 6 meters less than its length. the area is 72 square meters. find the dimensions of the rectangle. show answer the answer is \( w = 6, l = 12 \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l = w + 6, \, a = 72\) \(\,\,\,\,\, (w + 6)w = 72\) \(\,\,\,\,\, w^2 + 6w – 72 = 0\) \(\,\,\,\,\, (w + 12)(w – 6) = 0\) \(\,\,\,\,\, w = -12 \text{ or } w = 6\) \(\,\,\,\,\, l = 6 + 6 = 12 \text{ or } l = -12 + 6 = -6\) \(\,\,\,\,\, \text{width} = 6 \text{ meters}, \text{length} = 12 \text{ meters} \), \(\textbf{8)}\) the length of a rectangle is twice the width. the area is 32 square inches. find the dimensions of the rectangle. show answer the answer is \( w=4, l=8 \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l = 2w, \, a = 32\) \(\,\,\,\,\, (2w)w = 32\) \(\,\,\,\,\, 2w^2 = 32\) \(\,\,\,\,\, w^2 = 16\) \(\,\,\,\,\, w = 4\) \(\,\,\,\,\, l = 2(4) = 8\) \(\,\,\,\,\, \text{width} = 4 \text{ inches}, \text{length} = 8 \text{ inches} \), \(\textbf{9)}\) the length of a rectangle is 1 foot less than twice the width. the area is 120 square feet. find the dimensions of the rectangle. show answer the answer is \( w = 8, l = 15 \) show work \(\,\,\,\,\, \text{length } (l) \, \times \, \text{width } (w) = \text{area } (a)\) \(\,\,\,\,\, l = 2w – 1, \, a = 120\) \(\,\,\,\,\, (2w – 1)w = 120\) \(\,\,\,\,\, 2w^2 – w – 120 = 0\) \(\,\,\,\,\, (2w + 15)(w – 8) = 0\) \(\,\,\,\,\, w = -15/2 \text{ or } w = 8\) \(\,\,\,\,\, l = 2(8) – 1 = 16 – 1 = 15 \text{ or } l = 2(-15/2) – 1 = -15 – 1 = -16\) \(\,\,\,\,\, \text{width} = 8 \text{ feet}, \text{length} = 15 \text{ feet} \), \(\textbf{10)}\) the product of two positive consecutive integers is 56. find the integers. show answer the integers are \( 7, 8 \) show work let’s call the first integer “n” and the second integer “n + 1”. \(\,\,\,\,\, n(n + 1) = 56\) \(\,\,\,\,\, n^2 + n – 56 = 0\) \(\,\,\,\,\, (n + 8)(n – 7) = 0\) \(\,\,\,\,\, n = -8 \text{ or } n = 7\) since we’re looking for positive integers, the integers are \(7, 8\), \(\textbf{11)}\) the product of two positive consecutive odd integers is 99. find the integers. show answer the integers are \( 9, 11 \) show work let’s call the first odd integer “n” and the second odd integer “n + 2”. \(\,\,\,\,\, n(n + 2) = 99\) \(\,\,\,\,\, n^2 + 2n – 99 = 0\) \(\,\,\,\,\, (n + 11)(n – 9) = 0\) \(\,\,\,\,\, n = -11 \text{ or } n = 9\) since we’re looking for positive odd integers, the integers are \(9, 11\), \(\textbf{12)}\) the product of two positive consecutive odd integers is 1 less than 3 times their sum. find the integers. show answer the integers are \( 5, 7 \) show work let’s call the first odd integer “n” and the second odd integer “n + 2”. \(\,\,\,\,\, n(n + 2) = 3(n + n + 2) – 1\) \(\,\,\,\,\, n^2 + 2n = 6n + 6 – 1\) \(\,\,\,\,\, n^2 – 4n – 5 = 0\) \(\,\,\,\,\, (n – 5)(n + 1) = 0\) \(\,\,\,\,\, n = 5 \text{ or } n = -1\) since we’re looking for positive odd integers, the integers are \(5, 7\), \(\textbf{13)}\) the product of two positive consecutive integers is thirteen less than five times their sum. find the integers. show answer the answer is \( 8, 9 \) show work let’s call the first integer “n” and the second integer “n + 1”. \(\,\,\,\,\, n(n + 1) = 5(n + n + 1) – 13\) \(\,\,\,\,\, n^2 + n = 10n + 5 – 13\) \(\,\,\,\,\, n^2 – 9n – 8 = 0\) \(\,\,\,\,\, (n – 8)(n + 1) = 0\) \(\,\,\,\,\, n = 8 \text{ or } n = -1\) since we’re looking for positive integers, the integers are \(8, 9\), \(\textbf{14)}\) the product of two positive consecutive odd integers is 77 more than twice the larger. find the integers. show answer the integers are \( 9, 11 \) show work let’s call the first odd integer “n” and the second odd integer “n + 2”. \(\,\,\,\,\, n(n + 2) = 2(n + 2) + 77\) \(\,\,\,\,\, n^2 + 2n = 2n + 4 + 77\) \(\,\,\,\,\, n^2 – 75 = 0\) \(\,\,\,\,\, (n – 5)(n + 5) = 0\) \(\,\,\,\,\, n = 5 \text{ or } n = -5\) since we’re looking for positive odd integers, the integers are \(5, 7\), challenge problem, \(\textbf{15)}\) the width is twice the height. if the perimeter is 120, what is the area show area the area is \( 800\) units\(^2 \), see related pages\(\), \(\bullet\text{ adding and subtracting polynomials}\) \(\,\,\,\,\,\,\,\,(4d+7)−(2d−5)…\), \(\bullet\text{ multiplying polynomials}\) \(\,\,\,\,\,\,\,\,(x+2)(x^2+3x−5)…\), \(\bullet\text{ dividing polynomials}\) \(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\), \(\bullet\text{ dividing polynomials (synthetic division)}\) \(\,\,\,\,\,\,\,\,(x^3-8)÷(x-2)…\), \(\bullet\text{ synthetic substitution}\) \(\,\,\,\,\,\,\,\,f(x)=4x^4−3x^2+8x−2…\), \(\bullet\text{ end behavior}\) \(\,\,\,\,\,\,\,\, \text{as } x\rightarrow \infty, \quad f(x)\rightarrow \infty \) \(\,\,\,\,\,\,\,\, \text{as } x\rightarrow -\infty, \quad f(x)\rightarrow \infty… \), \(\bullet\text{ completing the square}\) \(\,\,\,\,\,\,\,\,x^2+10x−24=0…\), \(\bullet\text{ quadratic formula and the discriminant}\) \(\,\,\,\,\,\,\,\,x=-b \pm \displaystyle\frac{\sqrt{b^2-4ac}}{2a}…\), \(\bullet\text{ complex numbers}\) \(\,\,\,\,\,\,\,\,i=\sqrt{-1}…\), \(\bullet\text{ multiplicity of roots}\) \(\,\,\,\,\,\,\,\,\) \(…\), \(\bullet\text{ rational zero theorem}\) \(\,\,\,\,\,\,\,\, \pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 12…\), \(\bullet\text{ descartes rule of signs}\) \(\,\), \(\bullet\text{ roots and zeroes}\) \(\,\,\,\,\,\,\,\,\text{solve for }x. 3x^2+4x=0…\), \(\bullet\text{ linear factored form}\) \(\,\,\,\,\,\,\,\,f(x)=(x+4)(x+1)(x−3)…\), \(\bullet\text{ polynomial inequalities}\) \(\,\,\,\,\,\,\,\,x^3-4x^2-4x+16 \gt 0…\), doing quadratic word problems is a great way to reinforce the algebra behind quadratic equations. it also adds a fun element by demonstrating real-world applications., about andymath.com, andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. if you have any requests for additional content, please contact andy at [email protected] . he will promptly add the content. topics cover elementary math , middle school , algebra , geometry , algebra 2/pre-calculus/trig , calculus and probability/statistics . in the future, i hope to add physics and linear algebra content. visit me on youtube , tiktok , instagram and facebook . andymath content has a unique approach to presenting mathematics. the clear explanations, strong visuals mixed with dry humor regularly get millions of views. we are open to collaborations of all types, please contact andy at [email protected] for all enquiries. to offer financial support, visit my patreon page. let’s help students understand the math way of thinking thank you for visiting. how exciting, [latex]\textbf{10)}[/latex] words [latex]123[/latex] [showhide type="link1001" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{11)}[/latex] words [latex]123[/latex] [showhide type="link1101" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{14)}[/latex] words [latex]123[/latex] [showhide type="link1401" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{17)}[/latex] words [latex]123[/latex] [showhide type="link1701" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{19)}[/latex] words [latex]123[/latex] [showhide type="link1901" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{20)}[/latex] words [latex]123[/latex] [showhide type="link2001" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{21)}[/latex] words [latex]123[/latex] [showhide type="link2101" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{22)}[/latex] words [latex]123[/latex] [showhide type="link2201" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{23)}[/latex] words [latex]123[/latex] [showhide type="link2301" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{24)}[/latex] words [latex]123[/latex] [showhide type="link2401" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{25)}[/latex] words [latex]123[/latex] [showhide type="link2501" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{26)}[/latex] words [latex]123[/latex] [showhide type="link2601" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{27)}[/latex] words [latex]123[/latex] [showhide type="link2701" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{28)}[/latex] words [latex]123[/latex] [showhide type="link2801" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{29)}[/latex] words [latex]123[/latex] [showhide type="link2901" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide], [latex]\textbf{30)}[/latex] words [latex]123[/latex] [showhide type="link3001" more_text="show answer" less_text="" hidden="yes"] the answer is [latex] x=3 [/latex] [/showhide].