hypothesis testing statistics practice problems

Data Science Duniya

Learn Data Science, Machine Learning and Artificial Intelligence

Practice Problems on Hypothesis Testing

In this post I have put together the practice problems (from my academics study notes) to explain how in practical Hypothesis Testing works. This post is written mostly for the learners who want to deep dive into the statistics for data science. Focus will be on problem solving. For concepts please refer my previous posts on testing of hypothesis.

Prerequisite to understand Hypothesis testing examples:

Understanding of hypothesis testing concepts
How to use z-table, t-table and chi square table.

Formula list:

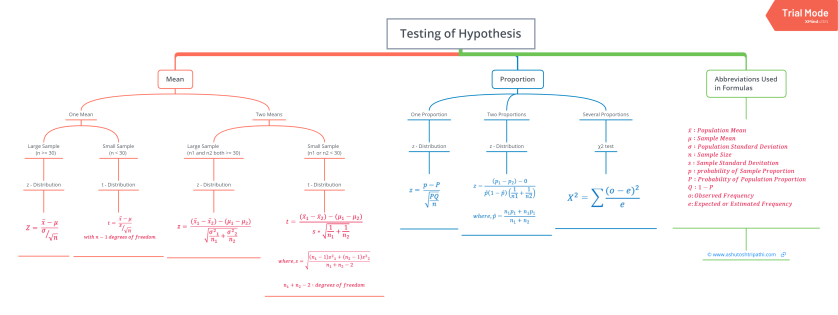
hypothesis testing statistics practice problems

Critical Regions

In hypothesis testing, critical region is represented by set of values, where null hypothesis is rejected. So it is also know as region of rejection. It takes different boundary values for different level of significance. Below info graphics shows the region of rejection that is critical region and region of acceptance with respect to the level of significance 1%.

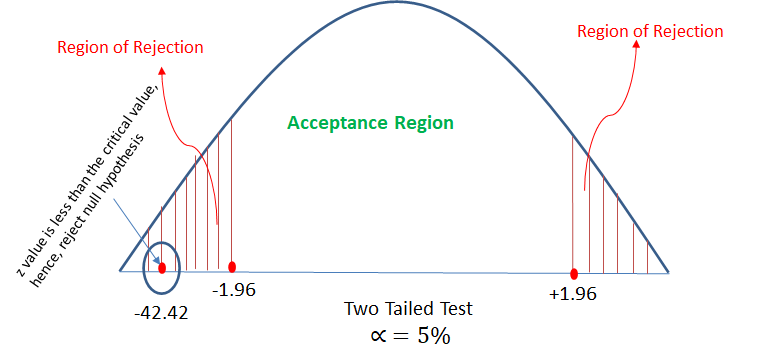
A Telecom service provider claims that individual customers pay on an average 400 rs. per month with standard deviation of 25 rs. A random sample of 50 customers bills during a given month is taken with a mean of 250 and standard deviation of 15. What to say with respect to the claim made by the service provider?

From the data available, it is observed that 400 out of 850 customers purchased the groceries online. Can we say that most of the customers are moving towards online shopping even for groceries?

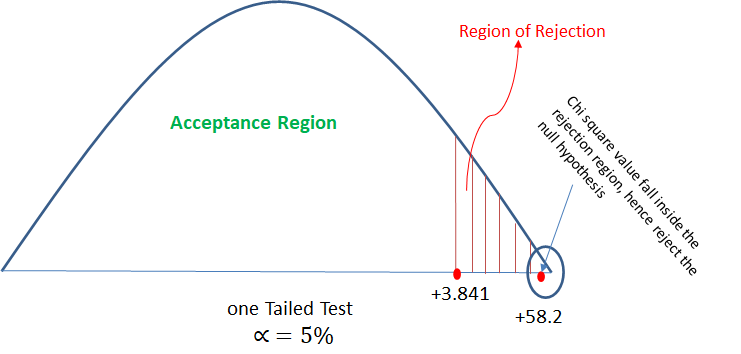
It is found that 250 errors in the randomly selected 1000 lines of code from Team A and 300 errors in 800 lines of code from Team B. Can we assume that team B’s performance is superior to that of A.

Following is the record of number of accidents took place during the various days of the week.

Can we conclude that accident s are independent of the day of week?

Analyze the below data and tell whether you can conclude that smoking causes cancer or not?

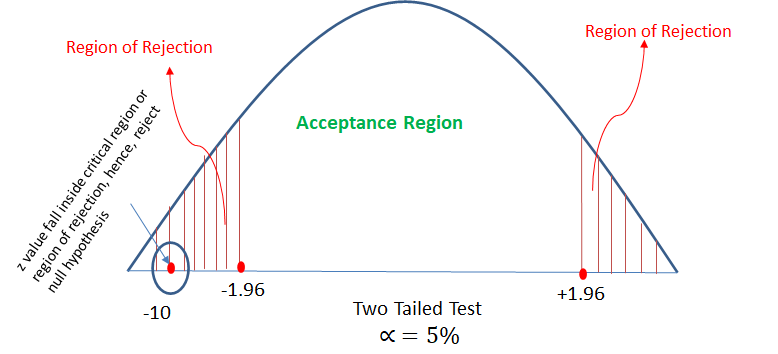
It is claimed that the mean of the population is 67 at 5% level of significance. Mean obtained from a random sample of size 100 is 64 with SD 3. Validate the claim.

There is an assumption that there is no significant difference between boys and girls with respect to intelligence. Tests are conducted on two groups and the following are the observations

Validate the claim with 5% LoS (Level of Significance)

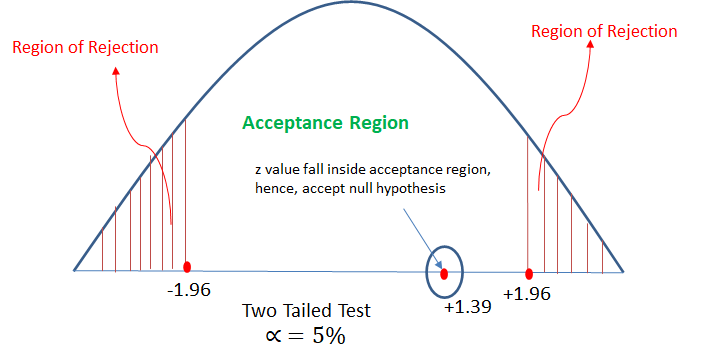
An automobile tyre manufacturer claims that the average life of a particular grade of tyre is more than 20,000 km. A random sample of 16 tyres is having mean 22,000 km with a standard deviation of 5000 km.

Validate the claim of the manufacturer at 5% LoS.

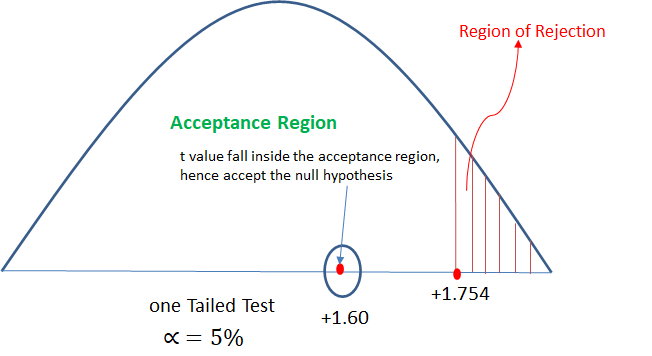
That is all for now. Please share your thoughts using the comment section below.

Hypothesis Testing Solved Examples(Questions and Solutions)

Here is a list hypothesis testing exercises and solutions. Try to solve a question by yourself first before you look at the solution.

Question 1 In the population, the average IQ is 100 with a standard deviation of 15. A team of scientists want to test a new medication to see if it has either a positive or negative effect on intelligence, or not effect at all. A sample of 30 participants who have taken the medication has a mean of 140. Did the medication affect intelligence? View Solution to Question 1

A professor wants to know if her introductory statistics class has a good grasp of basic math. Six students are chosen at random from the class and given a math proficiency test. The professor wants the class to be able to score above 70 on the test. The six students get the following scores:62, 92, 75, 68, 83, 95. Can the professor have 90% confidence that the mean score for the class on the test would be above 70. Solution to Question 2

Question 3 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.

Do the data provide sufficient evidence to conclude that, on the average, the new machine packs faster? Perform the required hypothesis test at the 5% level of significance. Solution to Question 3

Question 4 We want to compare the heights in inches of two groups of individuals. Here are the measurements: X: 175, 168, 168, 190, 156, 181, 182, 175, 174, 179 Y: 120, 180, 125, 188, 130, 190, 110, 185, 112, 188 Solution to Question 4

Question 5 A clinic provides a program to help their clients lose weight and asks a consumer agency to investigate the effectiveness of the program. The agency takes a sample of 15 people, weighing each person in the sample before the program begins and 3 months later. The results a tabulated below

Determine is the program is effective. Solution to Question 5

Question 6 A sample of 20 students were selected and given a diagnostic module prior to studying for a test. And then they were given the test again after completing the module. . The result of the students scores in the test before and after the test is tabulated below.

We want to see if there is significant improvement in the student’s performance due to this teaching method Solution to Question 6

Question 7 A study was performed to test wether cars get better mileage on premium gas than on regular gas. Each of 10 cars was first filled with regular or premium gas, decided by a coin toss, and the mileage for the tank was recorded. The mileage was recorded again for the same cars using other kind of gasoline. Determine wether cars get significantly better mileage with premium gas.

Mileage with regular gas: 16,20,21,22,23,22,27,25,27,28 Mileage with premium gas: 19, 22,24,24,25,25,26,26,28,32 Solution to Question 7

Question 8 An automatic cutter machine must cut steel strips of 1200 mm length. From a preliminary data, we checked that the lengths of the pieces produced by the machine can be considered as normal random variables with a 3mm standard deviation. We want to make sure that the machine is set correctly. Therefore 16 pieces of the products are randomly selected and weight. The figures were in mm: 1193,1196,1198,1195,1198,1199,1204,1193,1203,1201,1196,1200,1191,1196,1198,1191 Examine wether there is any significant deviation from the required size Solution to Question 8

Question 9 Blood pressure reading of ten patients before and after medication for reducing the blood pressure are as follows

Patient: 1,2,3,4,5,6,7,8,9,10 Before treatment: 86,84,78,90,92,77,89,90,90,86 After treatment: 80,80,92,79,92,82,88,89,92,83

Test the null hypothesis of no effect agains the alternate hypothesis that medication is effective. Execute it with Wilcoxon test Solution to Question 9

Question on ANOVA Sussan Sound predicts that students will learn most effectively with a constant background sound, as opposed to an unpredictable sound or no sound at all. She randomly divides 24 students into three groups of 8 each. All students study a passage of text for 30 minutes. Those in group 1 study with background sound at a constant volume in the background. Those in group 2 study with nose that changes volume periodically. Those in group 3 study with no sound at all. After studying, all students take a 10 point multiple choice test over the material. Their scores are tabulated below.

Group1: Constant sound: 7,4,6,8,6,6,2,9 Group 2: Random sound: 5,5,3,4,4,7,2,2 Group 3: No sound at all: 2,4,7,1,2,1,5,5 Solution to Question 10

Question 11 Using the following three groups of data, perform a one-way analysis of variance using α = 0.05.

Solution to Question 11

Question 12 In a packaging plant, a machine packs cartons with jars. It is supposed that a new machine would pack faster on the average than the machine currently used. To test the hypothesis, the time it takes each machine to pack ten cartons are recorded. The result in seconds is as follows.

New Machine: 42,41,41.3,41.8,42.4,42.8,43.2,42.3,41.8,42.7 Old Machine: 42.7,43.6,43.8,43.3,42.5,43.5,43.1,41.7,44,44.1

Perform an F-test to determine if the null hypothesis should be accepted. Solution to Question 12

Question 13 A random sample 500 U.S adults are questioned about their political affiliation and opinion on a tax reform bill. We need to test if the political affiliation and their opinon on a tax reform bill are dependent, at 5% level of significance. The observed contingency table is given below.

Solution to Question 13

Question 14 Can a dice be considered regular which is showing the following frequency distribution during 1000 throws?

Solution to Question 14

Solution to Question 15

Question 16 A newly developed muesli contains five types of seeds (A, B, C, D and E). The percentage of which is 35%, 25%, 20%, 10% and 10% according to the product information. In a randomly selected muesli, the following volume distribution was found.

Lets us decide about the null hypothesis whether the composition of the sample corresponds to the distribution indicated on the packaging at alpha = 0.1 significance level. Solution to Question 16

Question 17 A research team investigated whether there was any significant correlation between the severity of a certain disease runoff and the age of the patients. During the study, data for n = 200 patients were collected and grouped according to the severity of the disease and the age of the patient. The table below shows the result

Let us decided about the correlation between the age of the patients and the severity of disease progression. Solution to Question 17

Question 18 A publisher is interested in determine which of three book cover is most attractive. He interviews 400 people in each of the three states (California, Illinois and New York), and asks each person which of the cover he or she prefers. The number of preference for each cover is as follows:

Do these data indicate that there are regional differences in people’s preferences concerning these covers? Use the 0.05 level of significance. Solution to Question 18

Question 19 Trees planted along the road were checked for which ones are healthy(H) or diseased (D) and the following arrangement of the trees were obtained:

H H H H D D D H H H H H H H D D H H D D D

Test at the = 0.05 significance wether this arrangement may be regarded as random

Solution to Question 19

Question 20 Suppose we flip a coin n = 15 times and come up with the following arrangements

H T T T H H T T T T H H T H H

(H = head, T = tail)

Test at the alpha = 0.05 significance level whether this arrangement may be regarded as random.

Solution to Question 20

kindsonthegenius

You might also like, hypothesis testing problems – question 5 ( a clinic provides a program to…, hypothesis testing problems – question 4( we want to compare the heights of…, how to perform mann-witney u test(step by step) – hypothesis testing.

I am really impressed with your writing abilities as well as with the structure to your weblog. Is this a paid subject matter or did you modify it yourself?

Either way stay up the excellent high quality writing, it’s uncommon to look a great blog like this one these days..

Below are given the gain in weights (in lbs.) of pigs fed on two diet A and B Dieta 25 32 30 34 24 14 32 24 30 31 35 25 – – DietB 44 34 22 10 47 31 40 30 32 35 18 21 35 29

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.3 hypothesis testing examples.

Example: Right-Tailed Test
Example: Left-Tailed Test
Example: Two-Tailed Test

Brinell Hardness Scores

An engineer measured the Brinell hardness of 25 pieces of ductile iron that were subcritically annealed. The resulting data were:

The engineer hypothesized that the mean Brinell hardness of all such ductile iron pieces is greater than 170. Therefore, he was interested in testing the hypotheses:

H 0 : μ = 170 H A : μ > 170

The engineer entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

Descriptive Statistics

$\mu$: mean of Brinelli

Null hypothesis H₀: $\mu$ = 170 Alternative hypothesis H₁: $\mu$ > 170

The output tells us that the average Brinell hardness of the n = 25 pieces of ductile iron was 172.52 with a standard deviation of 10.31. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 10.31 by the square root of n = 25, is 2.06). The test statistic t * is 1.22, and the P -value is 0.117.

If the engineer set his significance level α at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were greater than 1.7109 (determined using statistical software or a t -table):

t distribution graph for df = 24 and a right tailed test of .05 significance level

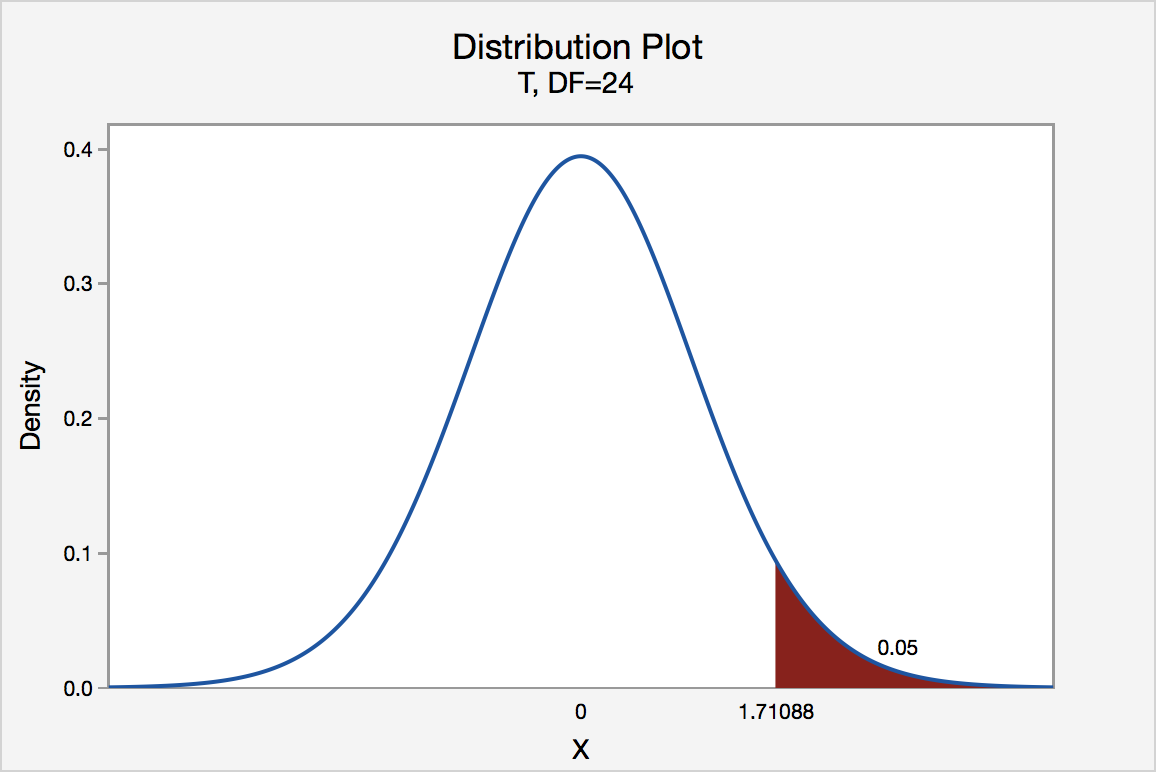
Since the engineer's test statistic, t * = 1.22, is not greater than 1.7109, the engineer fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

If the engineer used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 24 curve and to the right of the test statistic t * = 1.22:

t distribution graph of right tailed test showing the p-value of 0117 for a t-value of 1.22

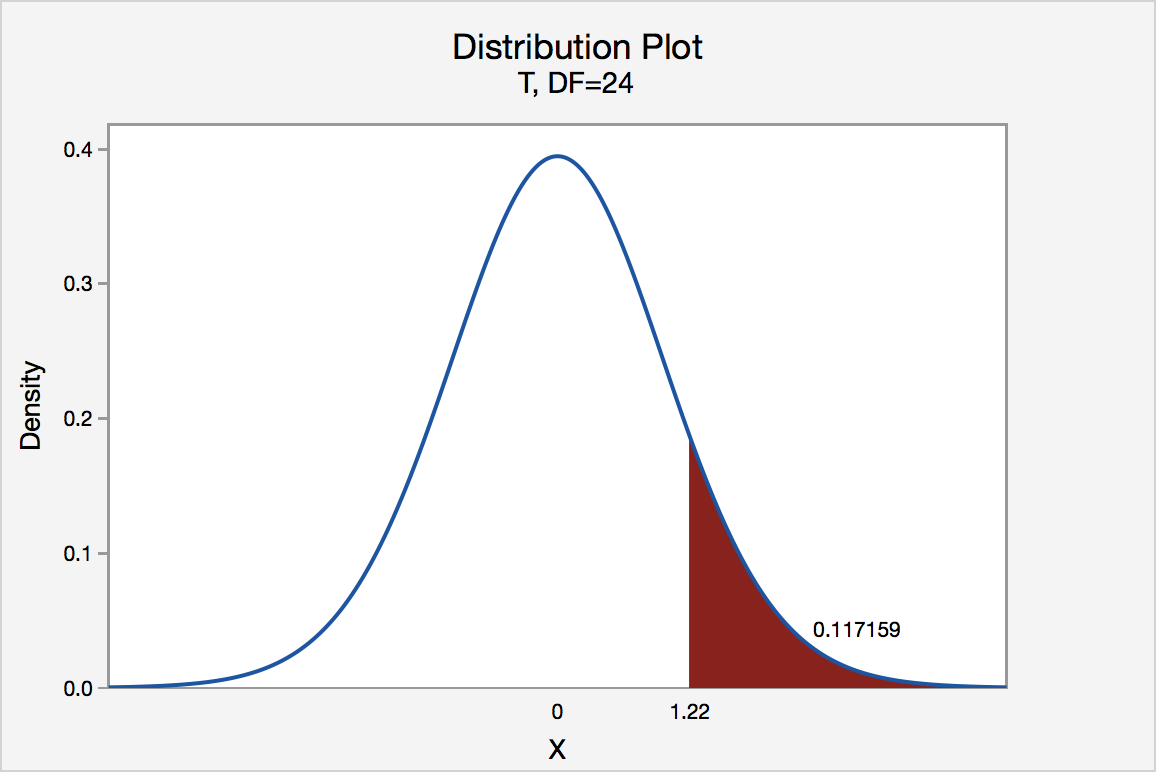
In the output above, Minitab reports that the P -value is 0.117. Since the P -value, 0.117, is greater than $\alpha$ = 0.05, the engineer fails to reject the null hypothesis. There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean Brinell hardness of all such ductile iron pieces is greater than 170.

Note that the engineer obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Height of Sunflowers

A biologist was interested in determining whether sunflower seedlings treated with an extract from Vinca minor roots resulted in a lower average height of sunflower seedlings than the standard height of 15.7 cm. The biologist treated a random sample of n = 33 seedlings with the extract and subsequently obtained the following heights:

The biologist's hypotheses are:

H 0 : μ = 15.7 H A : μ < 15.7

The biologist entered her data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. She obtained the following output:

$\mu$: mean of Height

Null hypothesis H₀: $\mu$ = 15.7 Alternative hypothesis H₁: $\mu$ < 15.7

The output tells us that the average height of the n = 33 sunflower seedlings was 13.664 with a standard deviation of 2.544. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 13.664 by the square root of n = 33, is 0.443). The test statistic t * is -4.60, and the P -value, 0.000, is to three decimal places.

Minitab Note. Minitab will always report P -values to only 3 decimal places. If Minitab reports the P -value as 0.000, it really means that the P -value is 0.000....something. Throughout this course (and your future research!), when you see that Minitab reports the P -value as 0.000, you should report the P -value as being "< 0.001."

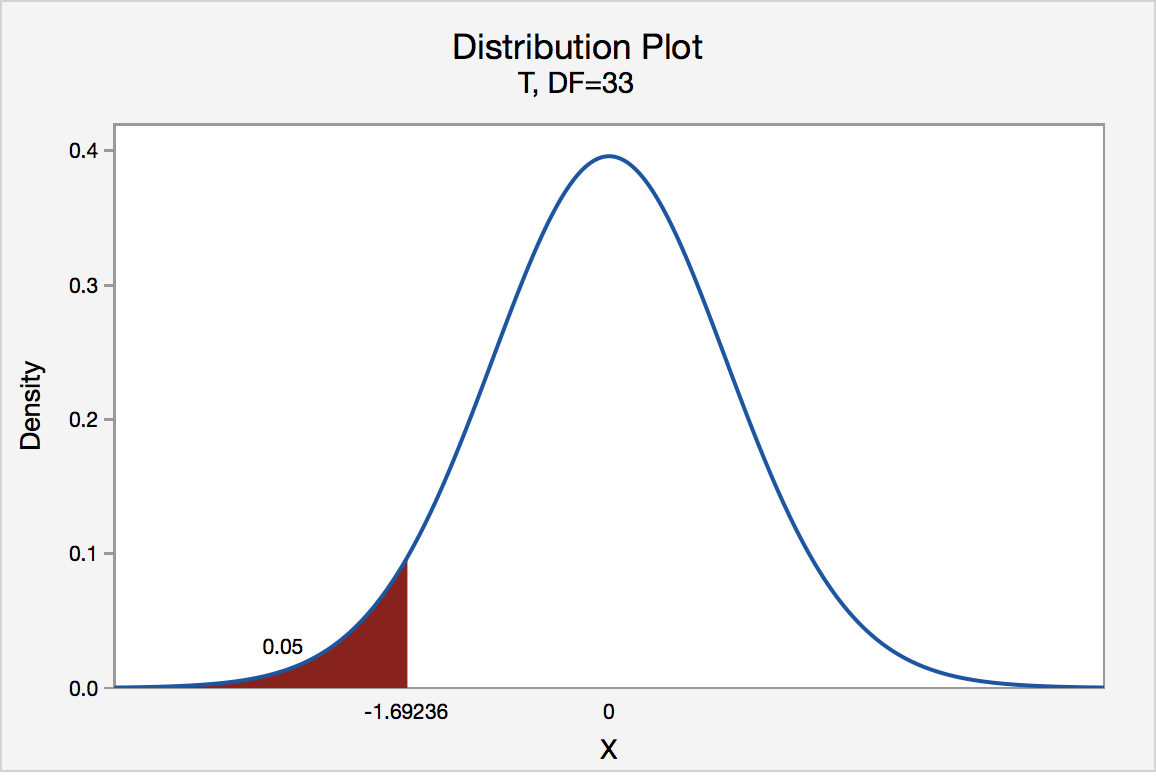
If the biologist set her significance level $\alpha$ at 0.05 and used the critical value approach to conduct her hypothesis test, she would reject the null hypothesis if her test statistic t * were less than -1.6939 (determined using statistical software or a t -table):s-3-3

Since the biologist's test statistic, t * = -4.60, is less than -1.6939, the biologist rejects the null hypothesis. That is, the test statistic falls in the "critical region." There is sufficient evidence, at the α = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

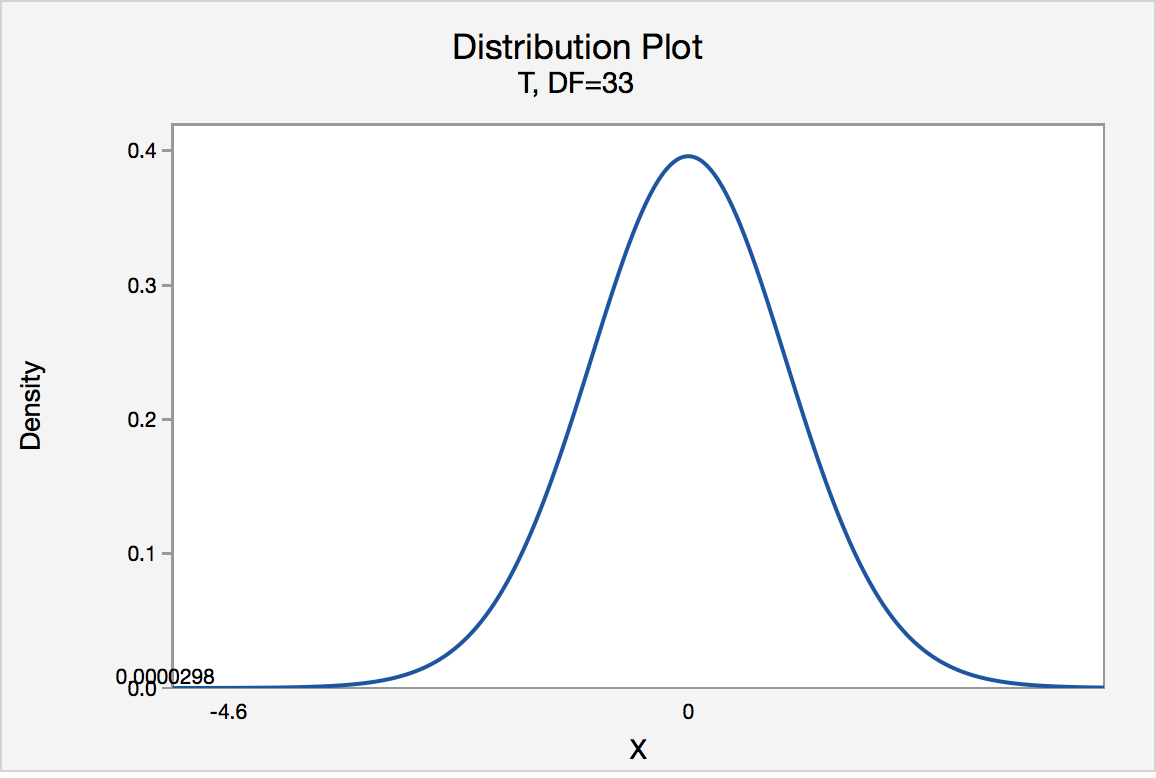
If the biologist used the P -value approach to conduct her hypothesis test, she would determine the area under a t n - 1 = t 32 curve and to the left of the test statistic t * = -4.60:

t-distribution for left tailed test with significance level of 0.05 shown in left tail

In the output above, Minitab reports that the P -value is 0.000, which we take to mean < 0.001. Since the P -value is less than 0.001, it is clearly less than $\alpha$ = 0.05, and the biologist rejects the null hypothesis. There is sufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean height of all such sunflower seedlings is less than 15.7 cm.

t-distribution graph for left tailed test with a t-value of -4.60 and left tail area of 0.000

Note again that the biologist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

Gum Thickness

A manufacturer claims that the thickness of the spearmint gum it produces is 7.5 one-hundredths of an inch. A quality control specialist regularly checks this claim. On one production run, he took a random sample of n = 10 pieces of gum and measured their thickness. He obtained:

The quality control specialist's hypotheses are:

H 0 : μ = 7.5 H A : μ ≠ 7.5

The quality control specialist entered his data into Minitab and requested that the "one-sample t -test" be conducted for the above hypotheses. He obtained the following output:

$\mu$: mean of Thickness

Null hypothesis H₀: $\mu$ = 7.5 Alternative hypothesis H₁: $\mu \ne$ 7.5

The output tells us that the average thickness of the n = 10 pieces of gums was 7.55 one-hundredths of an inch with a standard deviation of 0.1027. (The standard error of the mean "SE Mean", calculated by dividing the standard deviation 0.1027 by the square root of n = 10, is 0.0325). The test statistic t * is 1.54, and the P -value is 0.158.

If the quality control specialist sets his significance level $\alpha$ at 0.05 and used the critical value approach to conduct his hypothesis test, he would reject the null hypothesis if his test statistic t * were less than -2.2616 or greater than 2.2616 (determined using statistical software or a t -table):

t-distribution graph of two tails with a significance level of .05 and t values of -2.2616 and 2.2616

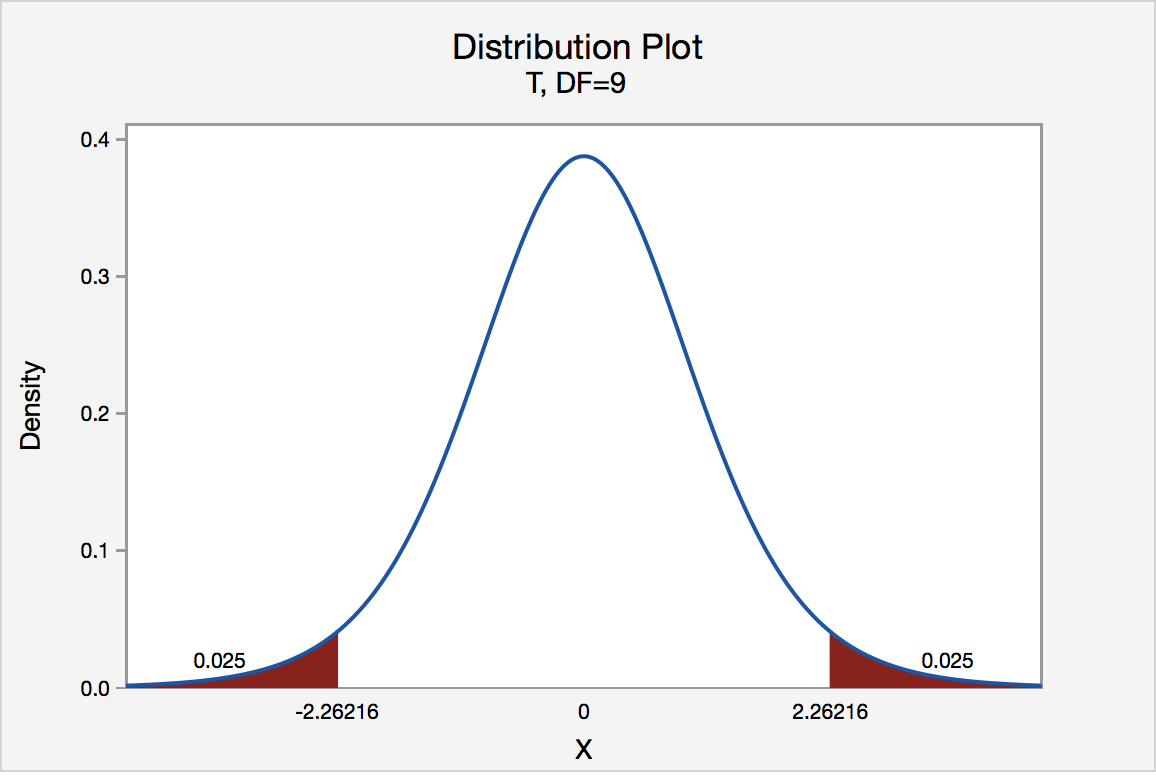
Since the quality control specialist's test statistic, t * = 1.54, is not less than -2.2616 nor greater than 2.2616, the quality control specialist fails to reject the null hypothesis. That is, the test statistic does not fall in the "critical region." There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean thickness of all of the manufacturer's spearmint gum differs from 7.5 one-hundredths of an inch.

If the quality control specialist used the P -value approach to conduct his hypothesis test, he would determine the area under a t n - 1 = t 9 curve, to the right of 1.54 and to the left of -1.54:

t-distribution graph for a two tailed test with t values of -1.54 and 1.54, the corresponding p-values are 0.0789732 on both tails

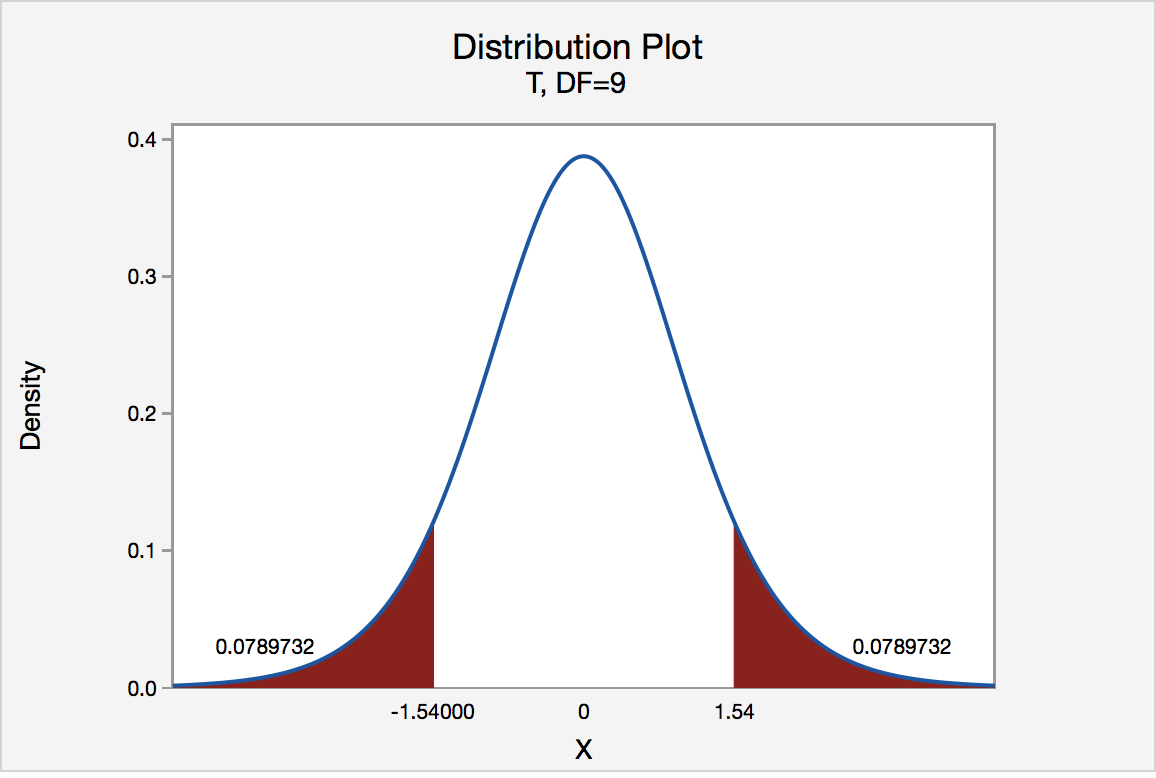
In the output above, Minitab reports that the P -value is 0.158. Since the P -value, 0.158, is greater than $\alpha$ = 0.05, the quality control specialist fails to reject the null hypothesis. There is insufficient evidence, at the $\alpha$ = 0.05 level, to conclude that the mean thickness of all pieces of spearmint gum differs from 7.5 one-hundredths of an inch.

Note that the quality control specialist obtains the same scientific conclusion regardless of the approach used. This will always be the case.

In our review of hypothesis tests, we have focused on just one particular hypothesis test, namely that concerning the population mean $\mu$. The important thing to recognize is that the topics discussed here — the general idea of hypothesis tests, errors in hypothesis testing, the critical value approach, and the P -value approach — generally extend to all of the hypothesis tests you will encounter.

Calcworkshop

Hypothesis Test Comprehensive Walkthrough

Advance Hypothesis Test Skills — Boost Statistical Savvy — Excel in Practical Situations