type 2 error in research methodology

Type 1 and Type 2 Errors in Statistics

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

On This Page:

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty). Because a p -value is based on probabilities, there is always a chance of making an incorrect conclusion regarding accepting or rejecting the null hypothesis ( H 0 ).

Anytime we make a decision using statistics, there are four possible outcomes, with two representing correct decisions and two representing errors.

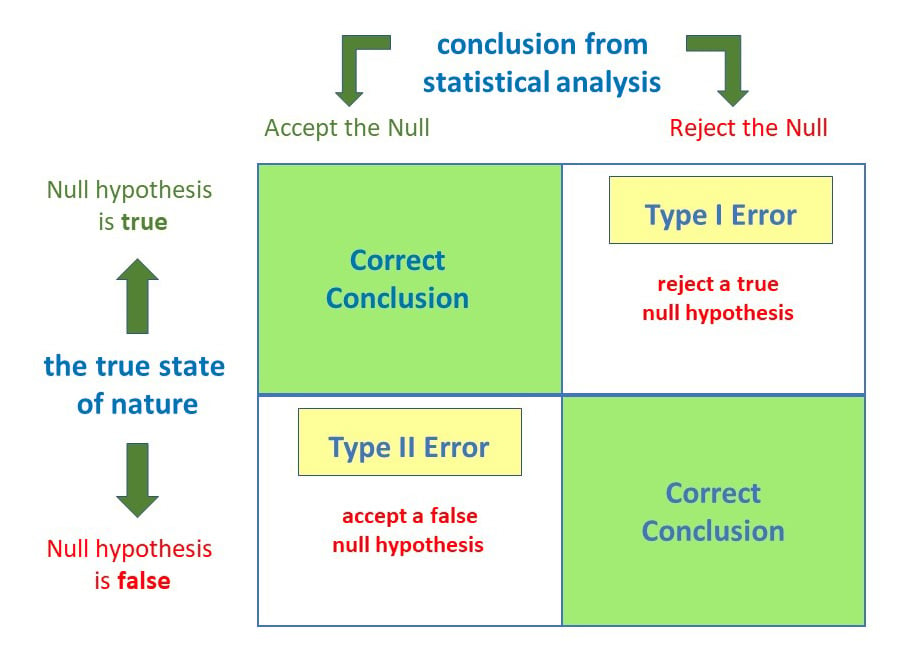
The chances of committing these two types of errors are inversely proportional: that is, decreasing type I error rate increases type II error rate and vice versa.

As the significance level (α) increases, it becomes easier to reject the null hypothesis, decreasing the chance of missing a real effect (Type II error, β). If the significance level (α) goes down, it becomes harder to reject the null hypothesis , increasing the chance of missing an effect while reducing the risk of falsely finding one (Type I error).

Type I error

A type 1 error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. Simply put, it’s a false alarm.

This means that you report that your findings are significant when they have occurred by chance.

The probability of making a type 1 error is represented by your alpha level (α), the p- value below which you reject the null hypothesis.

A p -value of 0.05 indicates that you are willing to accept a 5% chance of getting the observed data (or something more extreme) when the null hypothesis is true.

You can reduce your risk of committing a type 1 error by setting a lower alpha level (like α = 0.01). For example, a p-value of 0.01 would mean there is a 1% chance of committing a Type I error.

However, using a lower value for alpha means that you will be less likely to detect a true difference if one really exists (thus risking a type II error).

Scenario: Drug Efficacy Study

Imagine a pharmaceutical company is testing a new drug, named “MediCure”, to determine if it’s more effective than a placebo at reducing fever. They experimented with two groups: one receives MediCure, and the other received a placebo.

Null Hypothesis (H0) : MediCure is no more effective at reducing fever than the placebo.
Alternative Hypothesis (H1) : MediCure is more effective at reducing fever than the placebo.

After conducting the study and analyzing the results, the researchers found a p-value of 0.04.

If they use an alpha (α) level of 0.05, this p-value is considered statistically significant, leading them to reject the null hypothesis and conclude that MediCure is more effective than the placebo.

However, MediCure has no actual effect, and the observed difference was due to random variation or some other confounding factor. In this case, the researchers have incorrectly rejected a true null hypothesis.

Error : The researchers have made a Type 1 error by concluding that MediCure is more effective when it isn’t.

Implications

Resource Allocation : Making a Type I error can lead to wastage of resources. If a business believes a new strategy is effective when it’s not (based on a Type I error), they might allocate significant financial and human resources toward that ineffective strategy.

Unnecessary Interventions : In medical trials, a Type I error might lead to the belief that a new treatment is effective when it isn’t. As a result, patients might undergo unnecessary treatments, risking potential side effects without any benefit.

Reputation and Credibility : For researchers, making repeated Type I errors can harm their professional reputation. If they frequently claim groundbreaking results that are later refuted, their credibility in the scientific community might diminish.

Type II error

A type 2 error (or false negative) happens when you accept the null hypothesis when it should actually be rejected.

Here, a researcher concludes there is not a significant effect when actually there really is.

The probability of making a type II error is called Beta (β), which is related to the power of the statistical test (power = 1- β). You can decrease your risk of committing a type II error by ensuring your test has enough power.

You can do this by ensuring your sample size is large enough to detect a practical difference when one truly exists.

Scenario: Efficacy of a New Teaching Method

Educational psychologists are investigating the potential benefits of a new interactive teaching method, named “EduInteract”, which utilizes virtual reality (VR) technology to teach history to middle school students.

They hypothesize that this method will lead to better retention and understanding compared to the traditional textbook-based approach.

Null Hypothesis (H0) : The EduInteract VR teaching method does not result in significantly better retention and understanding of history content than the traditional textbook method.
Alternative Hypothesis (H1) : The EduInteract VR teaching method results in significantly better retention and understanding of history content than the traditional textbook method.

The researchers designed an experiment where one group of students learns a history module using the EduInteract VR method, while a control group learns the same module using a traditional textbook.

After a week, the student’s retention and understanding are tested using a standardized assessment.

Upon analyzing the results, the psychologists found a p-value of 0.06. Using an alpha (α) level of 0.05, this p-value isn’t statistically significant.

Therefore, they fail to reject the null hypothesis and conclude that the EduInteract VR method isn’t more effective than the traditional textbook approach.

However, let’s assume that in the real world, the EduInteract VR truly enhances retention and understanding, but the study failed to detect this benefit due to reasons like small sample size, variability in students’ prior knowledge, or perhaps the assessment wasn’t sensitive enough to detect the nuances of VR-based learning.

Error : By concluding that the EduInteract VR method isn’t more effective than the traditional method when it is, the researchers have made a Type 2 error.

This could prevent schools from adopting a potentially superior teaching method that might benefit students’ learning experiences.

Missed Opportunities : A Type II error can lead to missed opportunities for improvement or innovation. For example, in education, if a more effective teaching method is overlooked because of a Type II error, students might miss out on a better learning experience.

Potential Risks : In healthcare, a Type II error might mean overlooking a harmful side effect of a medication because the research didn’t detect its harmful impacts. As a result, patients might continue using a harmful treatment.

Stagnation : In the business world, making a Type II error can result in continued investment in outdated or less efficient methods. This can lead to stagnation and the inability to compete effectively in the marketplace.

How do Type I and Type II errors relate to psychological research and experiments?

Type I errors are like false alarms, while Type II errors are like missed opportunities. Both errors can impact the validity and reliability of psychological findings, so researchers strive to minimize them to draw accurate conclusions from their studies.

How does sample size influence the likelihood of Type I and Type II errors in psychological research?

Sample size in psychological research influences the likelihood of Type I and Type II errors. A larger sample size reduces the chances of Type I errors, which means researchers are less likely to mistakenly find a significant effect when there isn’t one.

A larger sample size also increases the chances of detecting true effects, reducing the likelihood of Type II errors.

Are there any ethical implications associated with Type I and Type II errors in psychological research?

Yes, there are ethical implications associated with Type I and Type II errors in psychological research.

Type I errors may lead to false positive findings, resulting in misleading conclusions and potentially wasting resources on ineffective interventions. This can harm individuals who are falsely diagnosed or receive unnecessary treatments.

Type II errors, on the other hand, may result in missed opportunities to identify important effects or relationships, leading to a lack of appropriate interventions or support. This can also have negative consequences for individuals who genuinely require assistance.

Therefore, minimizing these errors is crucial for ethical research and ensuring the well-being of participants.

Further Information

Publication manual of the American Psychological Association
Statistics for Psychology Book Download

Microbe Notes

Type I Error and Type II Error: 10 Differences, Examples

Type I Error and Type II Error with 10 Differences

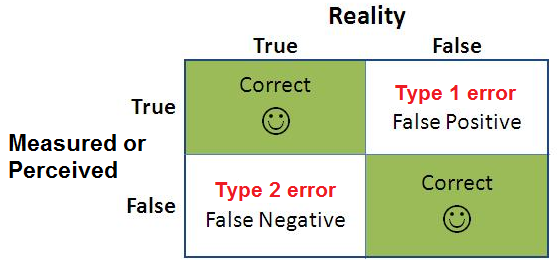
Image Source: AB Tasty .

Table of Contents

Interesting Science Videos

Type 1 error definition

Type 1 error, in statistical hypothesis testing, is the error caused by rejecting a null hypothesis when it is true.
Type 1 error is caused when the hypothesis that should have been accepted is rejected.
Type I error is denoted by α (alpha), known as an error, also called the level of significance of the test.
This type of error is a false positive error where the null hypothesis is rejected based on some error during the testing.
The null hypothesis is set to state that there is no relationship between two variables and the cause-effect relationship between two variables, if present, is caused by chance.
Type 1 error occurs when the null hypothesis is rejected even when there is no relationship between the variables.
As a result of this error, the researcher might believe that the hypothesis works even when it doesn’t.

Type 1 error causes

Type 1 error is caused when something other than the variable affects the other variable, which results in an outcome that supports the rejection of the null hypothesis.
Under such conditions, the outcome appears to have happened due to some causes than chance when it is caused by chance.
Before a hypothesis is tested, a probability is set as a level of significance which means that the hypothesis is being tested while taking a chance where the null hypothesis is rejected even when it is true.
Thus, type 1 error might be due to the chance/ level of significance set before the test without considering the test duration and sample size.

Probability of type 1 error

The probability of Type I error is usually determined in advance and is understood as the significance level of testing the hypothesis.
If the Type I error is fixed at 5 percent, there are about five chances in 100 that the null hypothesis, H0, will be rejected when it is true.
The rate or probability of type 1 error is symbolized by α and is also termed the level os significance in a test.
It is possible to reduce type 1 error at a fixed size of the sample; however, while doing so, the probability of type II error increases.
There is a trade-off between the two errors where decreasing the probability of one error increases the probability of another. It is not possible to reduce both errors simultaneously.
Thus, depending on the type and nature of the test, the researchers need to decide the appropriate level of type 1 error after evaluating the consequences of the errors.

Type 1 error examples

For this, let us take a hypothesis where a player is trying to find the relationship between him wearing new shoes and the number of wins for his team.
Here, if the number of wins for his team is more when he was wearing his new shoes is more than the number of wins for his team otherwise, he might accept the alternative hypothesis and determine that there is a relationship.
However, the winning of his team might be influenced by just chance rather than his shoes which results in a type 1 error.
In this case, he should’ve accepted the null hypothesis because the winning of a team might happen due to chance or luck.

Type II error definition

Type II error is the error that occurs when the null hypothesis is accepted when it is not true.
In simple words, Type II error means accepting the hypothesis when it should not have been accepted.
The type II error results in a false negative result.
In other words, type II is the error of failing to accept an alternative hypothesis when the researcher doesn’t have adequate power.
The Type II error is denoted by β (beta) and is also termed the beta error.
The null hypothesis states that there is no relationship between two variables, and the cause-effect relationship between two variables, if present, is caused by chance.
Type II error occurs when the null hypothesis is acceptable considering that the relationship between the variables is because of chance or luck, and even when there is a relationship between the variables.
As a result of this error, the researcher might believe that the hypothesis doesn’t work even when it should.

Type II error causes

The primary cause of type II error, like a Type II error, is the low power of the statistical test.
This occurs when the statistical is not powerful and thus results in a Type II error.
Other factors, like the sample size, might also affect the test results.
When small sample size is selected, the relationship between the two variables being tested might not be significant even when it does exist.
The researcher might assume the relationship is due to chance and thus reject the alternative hypothesis even when it is true.
There it is important to select an appropriate size of the sample before beginning the test.

Probability of type II error

The probability of committing a Type II error is calculated by subtracting the power of the test from 1.
If Type II error is fixed at 2 percent, there are about two chances in 100 that the null hypothesis, H0, will be accepted when it is not true.
The rate or probability of type II error is symbolized by β and is also termed the error of the second type.
It is possible to reduce the probability of Type II error by increasing the significance level.
In this case, the probability of rejecting the null hypothesis even when it is true also increases, decreasing the chances of accepting the null hypothesis when it is not true.
However, because type I and Type II error are interconnected, reducing one tends to increase the probability of the other.
Therefore, depending on the nature of the test, it is important to determine which one of the errors is less detrimental to the test.
For this, if a type I error involves the time and effort of retesting the chemicals used in medicine, that should have been accepted. In contrast, the type II error involves the chances of several users of this medicine being poisoned, and it is wise to accept the type I error over type II.

Type II error examples

For this, let us take a hypothesis where a shepherd thinks there is no wolf in the village, and he wakes up all night for five nights to determine the wolf’s existence.
If he sees no wolf for five nights, he might assume that there is no wolf in the village where the wolf might exist and attack the sixth night.
In this case, when the shepherd accepts that no wolf exists, a type II error results where he agrees with the null hypothesis even when it is not true.

Graphical representation of type 1 and type 2 errors

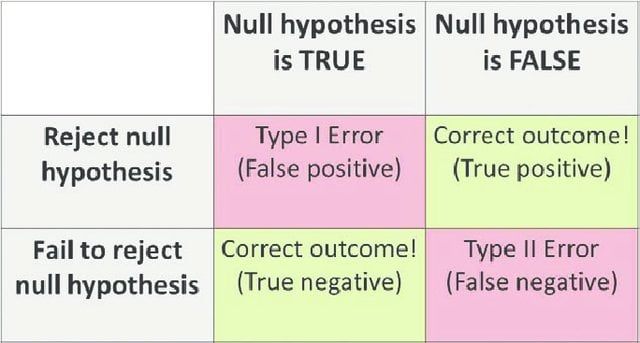
Type I Error vs. Type II Error

Type i error vs. type ii error video.

References and Sources

R. Kothari (1990) Research Methodology. Vishwa Prakasan. India.
https://magoosh.com/statistics/type-i-error-definition-and-examples/
https://corporatefinanceinstitute.com/resources/knowledge/other/type-ii-error/
https://keydifferences.com/difference-between-type-i-and-type-ii-errors.html
3% – https://www.investopedia.com/terms/t/type-ii-error.asp
1% – https://www.thoughtco.com/null-hypothesis-examples-609097
1% – https://www.thoughtco.com/hypothesis-test-example-3126384
1% – https://www.stt.msu.edu/~lepage/STT200_Sp10/3-1-10key.pdf
1% – https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2996198/
1% – https://www.chegg.com/homework-help/questions-and-answers/following-table-shows-number-wins-eight-teams-football-season-also-shown-average-points-te-q13303251
1% – https://stattrek.com/hypothesis-test/power-of-test.aspx
1% – https://statisticsbyjim.com/hypothesis-testing/failing-reject-null-hypothesis/
1% – https://simplyeducate.me/2014/05/29/what-is-a-statistically-significant-relationship-between-two-variables/
1% – https://abrarrazakhan.files.wordpress.com/2014/04/mcq-testing-of-hypothesis-with-correct-answers.pdf
<1% – https://www.nature.com/articles/s41524-017-0047-6
<1% – https://www.dummies.com/education/math/statistics/understanding-type-i-and-type-ii-errors/
<1% – https://www.chegg.com/homework-help/questions-and-answers/null-hypothesis-true-possibility-making-type-error-true-false-believe-s-false-want-make-su-q4115439
<1% – https://stepupanalytics.com/hypothesis-testing-examples/
<1% – https://statistics.laerd.com/statistical-guides/hypothesis-testing-3.php
<1% – https://mpra.ub.uni-muenchen.de/66373/1/MPRA_paper_66373.pdf
<1% – https://en.wikipedia.org/wiki/Probability_of_error
<1% – https://educationalresearchtechniques.com/2016/02/03/type-i-and-type-ii-error/