null hypothesis for independent t test

t-test Calculator

Table of contents

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

When to use a t-test?

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

• A one-sample t-test;
• A two-sample t-test; and
• A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

• The data points are independent; AND
• The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Which t-test?

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Two-sample t-test

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

Paired t-test

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

How to do a t-test?

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

p-value from t-test

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

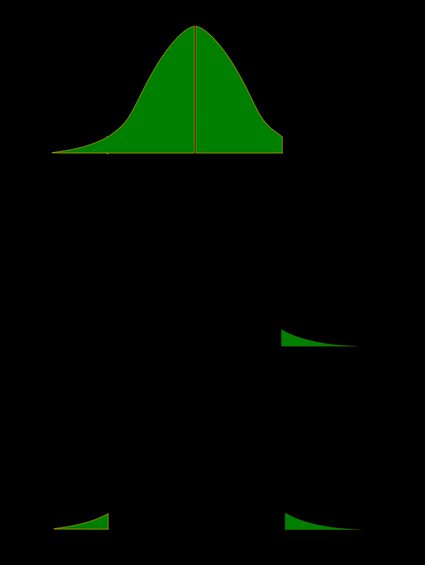
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

t-test critical values

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

How to use our t-test calculator

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

One-sample t-test

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 ​ .

The alternative hypothesis is that the population mean is:

• different from μ 0 \mu_0 μ 0 ​ ;
• smaller than μ 0 \mu_0 μ 0 ​ ; or
• greater than μ 0 \mu_0 μ 0 ​ .

One-sample t-test formula :

• μ 0 \mu_0 μ 0 ​ — Mean postulated in the null hypothesis;
• n n n — Sample size;
• x ˉ \bar{x} x ˉ — Sample mean; and
• s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 ​ , and μ 2 \mu_2 μ 2 ​ , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 ​ − μ 2 ​ is:

• Different from Δ \Delta Δ ;
• Smaller than Δ \Delta Δ ; or
• Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

• μ 1 \mu_1 μ 1 ​ and μ 2 \mu_2 μ 2 ​ are different from one another;
• μ 1 \mu_1 μ 1 ​ is smaller than μ 2 \mu_2 μ 2 ​ ; and
• μ 1 \mu_1 μ 1 ​ is greater than μ 2 \mu_2 μ 2 ​ .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p ​ is the so-called pooled standard deviation , which we compute as:

• Δ \Delta Δ — Mean difference postulated in the null hypothesis;
• n 1 n_1 n 1 ​ — First sample size;
• x ˉ 1 \bar{x}_1 x ˉ 1 ​ — Mean for the first sample;
• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• n 2 n_2 n 2 ​ — Second sample size;
• x ˉ 2 \bar{x}_2 x ˉ 2 ​ — Mean for the second sample; and
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 ​ + n 2 ​ − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

• s 1 s_1 s 1 ​ — Standard deviation in the first sample;
• s 2 s_2 s 2 ​ — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 ​ − 1 and n 2 − 1 n_2 - 1 n 2 ​ − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

• The pre- and post-means are different from one another (treatment has some effect);
• The pre-mean is smaller than the post-mean (treatment increases the result); or
• The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 ​ , ... , x n ​ be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 ​ , ... , y n ​ the respective post observations. That is, x i , y i x_i, y_i x i ​ , y i ​ are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i ​ := x i ​ − y i ​ . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 ​ , ... , d n ​ . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s  — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

t-test vs Z-test

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

• One-sample t-test;
• Two-sample t-test; and
• Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

• Subtract the null hypothesis mean from the sample mean value.
• Divide the difference by the standard deviation of the sample.
• Multiply the resultant with the square root of the sample size.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1h42f0z{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1h42f0z .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1h42f0z .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1h42f0z .katex .katex-version::after{content:'0.13.13';}.css-1h42f0z .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1h42f0z .katex .katex-html>.newline{display:block;}.css-1h42f0z .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1h42f0z .katex .strut{display:inline-block;}.css-1h42f0z .katex .textbf{font-weight:bold;}.css-1h42f0z .katex .textit{font-style:italic;}.css-1h42f0z .katex .textrm{font-family:KaTeX_Main;}.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .texttt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1h42f0z .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1h42f0z .katex .mathrm{font-style:normal;}.css-1h42f0z .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1h42f0z .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1h42f0z .katex .amsrm{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathbb,.css-1h42f0z .katex .textbb{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1h42f0z .katex .mathfrak,.css-1h42f0z .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1h42f0z .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathscr,.css-1h42f0z .katex .textscr{font-family:KaTeX_Script;}.css-1h42f0z .katex .mathsf,.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .mathboldsf,.css-1h42f0z .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1h42f0z .katex .mathitsf,.css-1h42f0z .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1h42f0z .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1h42f0z .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1h42f0z .katex .vlist-r{display:table-row;}.css-1h42f0z .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1h42f0z .katex .vlist>span{display:block;height:0;position:relative;}.css-1h42f0z .katex .vlist>span>span{display:inline-block;}.css-1h42f0z .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1h42f0z .katex .vlist-t2{margin-right:-2px;}.css-1h42f0z .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1h42f0z .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1h42f0z .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1h42f0z .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1h42f0z .katex .msupsub{text-align:left;}.css-1h42f0z .katex .mfrac>span>span{text-align:center;}.css-1h42f0z .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .mfrac .frac-line,.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline,.css-1h42f0z .katex .hdashline,.css-1h42f0z .katex .rule{min-height:1px;}.css-1h42f0z .katex .mspace{display:inline-block;}.css-1h42f0z .katex .llap,.css-1h42f0z .katex .rlap,.css-1h42f0z .katex .clap{width:0;position:relative;}.css-1h42f0z .katex .llap>.inner,.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{position:absolute;}.css-1h42f0z .katex .llap>.fix,.css-1h42f0z .katex .rlap>.fix,.css-1h42f0z .katex .clap>.fix{display:inline-block;}.css-1h42f0z .katex .llap>.inner{right:0;}.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{left:0;}.css-1h42f0z .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1h42f0z .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1h42f0z .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1h42f0z .katex .sizing.reset-size1.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size1.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size1.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1h42f0z .katex .sizing.reset-size1.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size1.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size1.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size1.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size1.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size1.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1h42f0z .katex .sizing.reset-size1.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1h42f0z .katex .sizing.reset-size1.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1h42f0z .katex .sizing.reset-size2.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size2.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size2.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1h42f0z .katex .sizing.reset-size2.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size2.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size2.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1h42f0z .katex .sizing.reset-size2.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size2.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size2.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size2.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1h42f0z .katex .sizing.reset-size2.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1h42f0z .katex .sizing.reset-size3.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1h42f0z .katex .sizing.reset-size3.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size3.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1h42f0z .katex .sizing.reset-size3.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1h42f0z .katex .sizing.reset-size3.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1h42f0z .katex .sizing.reset-size3.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1h42f0z .katex .sizing.reset-size3.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1h42f0z .katex .sizing.reset-size3.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1h42f0z .katex .sizing.reset-size3.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1h42f0z .katex .sizing.reset-size4.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size4.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size4.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1h42f0z .katex .sizing.reset-size4.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size4.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1h42f0z .katex .sizing.reset-size4.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1h42f0z .katex .sizing.reset-size4.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size4.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size4.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1h42f0z .katex .sizing.reset-size4.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1h42f0z .katex .sizing.reset-size4.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1h42f0z .katex .sizing.reset-size5.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size5.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size5.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1h42f0z .katex .sizing.reset-size5.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1h42f0z .katex .sizing.reset-size5.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size5.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1h42f0z .katex .sizing.reset-size5.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size5.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size5.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1h42f0z .katex .sizing.reset-size5.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1h42f0z .katex .sizing.reset-size5.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1h42f0z .katex .sizing.reset-size6.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size6.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1h42f0z .katex .sizing.reset-size6.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1h42f0z .katex .sizing.reset-size6.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1h42f0z .katex .sizing.reset-size6.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1h42f0z .katex .sizing.reset-size6.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size6.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size6.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size6.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1h42f0z .katex .sizing.reset-size6.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1h42f0z .katex .sizing.reset-size6.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1h42f0z .katex .sizing.reset-size7.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size7.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size7.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1h42f0z .katex .sizing.reset-size7.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size7.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size7.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size7.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size7.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size7.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size7.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1h42f0z .katex .sizing.reset-size7.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1h42f0z .katex .sizing.reset-size8.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size8.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size8.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1h42f0z .katex .sizing.reset-size8.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size8.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size8.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size8.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size8.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size8.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size8.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1h42f0z .katex .sizing.reset-size8.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1h42f0z .katex .sizing.reset-size9.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1h42f0z .katex .sizing.reset-size9.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size9.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1h42f0z .katex .sizing.reset-size9.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1h42f0z .katex .sizing.reset-size9.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1h42f0z .katex .sizing.reset-size9.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1h42f0z .katex .sizing.reset-size9.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size9.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size9.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size9.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1h42f0z .katex .sizing.reset-size9.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1h42f0z .katex .sizing.reset-size10.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1h42f0z .katex .sizing.reset-size10.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1h42f0z .katex .sizing.reset-size10.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1h42f0z .katex .sizing.reset-size10.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1h42f0z .katex .sizing.reset-size10.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1h42f0z .katex .sizing.reset-size10.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1h42f0z .katex .sizing.reset-size10.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1h42f0z .katex .sizing.reset-size10.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1h42f0z .katex .sizing.reset-size10.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1h42f0z .katex .sizing.reset-size10.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size10.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1h42f0z .katex .sizing.reset-size11.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1h42f0z .katex .sizing.reset-size11.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1h42f0z .katex .sizing.reset-size11.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1h42f0z .katex .sizing.reset-size11.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1h42f0z .katex .sizing.reset-size11.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1h42f0z .katex .sizing.reset-size11.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1h42f0z .katex .sizing.reset-size11.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1h42f0z .katex .sizing.reset-size11.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1h42f0z .katex .sizing.reset-size11.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1h42f0z .katex .sizing.reset-size11.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1h42f0z .katex .sizing.reset-size11.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1h42f0z .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1h42f0z .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1h42f0z .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1h42f0z .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1h42f0z .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1h42f0z .katex .delimcenter{position:relative;}.css-1h42f0z .katex .op-symbol{position:relative;}.css-1h42f0z .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1h42f0z .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1h42f0z .katex .op-limits>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent .accent-body{position:relative;}.css-1h42f0z .katex .accent .accent-body:not(.accent-full){width:0;}.css-1h42f0z .katex .overlay{display:block;}.css-1h42f0z .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1h42f0z .katex .mtable .arraycolsep{display:inline-block;}.css-1h42f0z .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1h42f0z .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1h42f0z .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1h42f0z .katex .svg-align{text-align:left;}.css-1h42f0z .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1h42f0z .katex svg path{stroke:none;}.css-1h42f0z .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1h42f0z .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1h42f0z .katex .stretchy::before,.css-1h42f0z .katex .stretchy::after{content:'';}.css-1h42f0z .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1h42f0z .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1h42f0z .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .x-arrow-pad{padding:0 0.5em;}.css-1h42f0z .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1h42f0z .katex .x-arrow,.css-1h42f0z .katex .mover,.css-1h42f0z .katex .munder{text-align:center;}.css-1h42f0z .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1h42f0z .katex .fbox,.css-1h42f0z .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1h42f0z .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1h42f0z .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1h42f0z .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1h42f0z .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1h42f0z .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1h42f0z .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1h42f0z .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1h42f0z .katex .mtr-glue{width:50%;}.css-1h42f0z .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1h42f0z .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1h42f0z .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1h42f0z .katex-display{display:block;margin:1em 0;text-align:center;}.css-1h42f0z .katex-display>.katex{display:block;white-space:nowrap;}.css-1h42f0z .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1h42f0z .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1h42f0z .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1h42f0z .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1h42f0z body{counter-reset:katexEqnNo mmlEqnNo;}.css-1h42f0z .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1h42f0z code,.css-1h42f0z kbd,.css-1h42f0z pre,.css-1h42f0z samp{font-family:monospace;}.css-1h42f0z code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1h42f0z figcaption,.css-1h42f0z caption{text-align:center;}.css-1h42f0z figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1h42f0z h3{font-size:1.75rem;}.css-1h42f0z h4{font-size:1.5rem;}.css-1h42f0z .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1h42f0z .mathBlock .katex{font-size:24px;text-align:left;}.css-1h42f0z .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1h42f0z .videoBlock,.css-1h42f0z .imageBlock{margin-bottom:16px;}.css-1h42f0z .imageBlock__image-align--left,.css-1h42f0z .videoBlock__video-align--left{float:left;}.css-1h42f0z .imageBlock__image-align--right,.css-1h42f0z .videoBlock__video-align--right{float:right;}.css-1h42f0z .imageBlock__image-align--center,.css-1h42f0z .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1h42f0z .imageBlock__image-align--none,.css-1h42f0z .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-1h42f0z .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1h42f0z .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1h42f0z .videoBlock__caption{text-align:left;}.css-1h42f0z table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1h42f0z .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1h42f0z .tableBlock thead,.css-1h42f0z .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1h42f0z .tableBlock th,.css-1h42f0z .tableBlock td{padding:10px;text-align:left;}.css-1h42f0z .tableBlock th{font-weight:bold!important;}.css-1h42f0z .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1h42f0z .tableBlock caption>p{margin:0;}.css-1h42f0z .tableBlock th>p,.css-1h42f0z .tableBlock td>p{margin:0;}.css-1h42f0z .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1h42f0z .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1h42f0z .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1h42f0z .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1h42f0z .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1h42f0z .tableBlock [data-text-align='center']{text-align:center;}.css-1h42f0z .tableBlock [data-text-align='left']{text-align:left;}.css-1h42f0z .tableBlock [data-text-align='right']{text-align:right;}.css-1h42f0z .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1h42f0z .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1h42f0z .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1h42f0z .tableBlock__font-size--xxsmall{font-size:10px;}.css-1h42f0z .tableBlock__font-size--xsmall{font-size:12px;}.css-1h42f0z .tableBlock__font-size--small{font-size:14px;}.css-1h42f0z .tableBlock__font-size--large{font-size:18px;}.css-1h42f0z .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--bordered td,.css-1h42f0z .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--borderless tbody+tbody,.css-1h42f0z .tableBlock__border--borderless td,.css-1h42f0z .tableBlock__border--borderless th,.css-1h42f0z .tableBlock__border--borderless tr,.css-1h42f0z .tableBlock__border--borderless thead,.css-1h42f0z .tableBlock__border--borderless thead th{border:0!important;}.css-1h42f0z .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-1h42f0z .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1h42f0z .tableBlock__table-compactl th,.css-1h42f0z .tableBlock__table-compact td{padding:3px!important;}.css-1h42f0z .tableBlock__full-size{width:100%;}.css-1h42f0z .textBlock{margin-bottom:16px;}.css-1h42f0z .textBlock__text-formatting--finePrint{font-size:12px;}.css-1h42f0z .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1h42f0z .textBlock__text-infoBox p{margin:0;}.css-1h42f0z .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1h42f0z .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1h42f0z .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1h42f0z .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1h42f0z .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1h42f0z .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1h42f0z .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1h42f0z.css-1h42f0z{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1h42f0z.css-1h42f0z:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1h42f0z .js-external-link-button.link-like,.css-1h42f0z .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .js-external-link-button.link-like:hover,.css-1h42f0z .js-external-link-anchor:hover,.css-1h42f0z .js-external-link-button.link-like:active,.css-1h42f0z .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1h42f0z .js-external-link-button.link-like:focus-visible,.css-1h42f0z .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1h42f0z p,.css-1h42f0z div{margin:0;display:block;}.css-1h42f0z pre{margin:0;display:block;}.css-1h42f0z pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1h42f0z pre:not(:first-child){padding-top:8px;}.css-1h42f0z ul,.css-1h42f0z ol{display:block margin:0;padding-left:20px;}.css-1h42f0z ul li,.css-1h42f0z ol li{padding-top:8px;}.css-1h42f0z ul ul,.css-1h42f0z ol ul,.css-1h42f0z ul ol,.css-1h42f0z ol ol{padding-top:0;}.css-1h42f0z ul:not(:first-child),.css-1h42f0z ol:not(:first-child){padding-top:4px;} Test setup

Choose test type

t-test for the population mean, μ, based on one independent sample . Null hypothesis H 0 : μ = μ 0  

Alternative hypothesis H 1

Test details

Significance level α

The probability that we reject a true H 0 (type I error).

Degrees of freedom

Calculated as sample size minus one.

Test results

• Flashes Safe Seven
• FlashLine Login
• Faculty & Staff Phone Directory
• Emeriti or Retiree
• All Departments
• Maps & Directions

• Building Guide
• Departments
• Directions & Parking
• Faculty & Staff
• Give to University Libraries
• Library Instructional Spaces
• Mission & Vision
• Newsletters
• Circulation
• Course Reserves / Core Textbooks
• Equipment for Checkout
• Interlibrary Loan
• Library Instruction
• Library Tutorials
• My Library Account
• Open Access Kent State
• Research Support Services
• Statistical Consulting
• Student Multimedia Studio
• Citation Tools
• Databases A-to-Z
• Databases By Subject
• Digital Collections
• Discovery@Kent State
• Government Information
• Journal Finder
• Library Guides
• Connect from Off-Campus
• Library Workshops
• Subject Librarians Directory
• Suggestions/Feedback
• Writing Commons
• Academic Integrity
• Jobs for Students
• International Students
• Meet with a Librarian
• Study Spaces
• University Libraries Student Scholarship
• Affordable Course Materials
• Copyright Services
• Selection Manager
• Suggest a Purchase

Library Locations at the Kent Campus

• Architecture Library
• Fashion Library
• Map Library
• Performing Arts Library
• Special Collections and Archives

Regional Campus Libraries

• East Liverpool
• College of Podiatric Medicine

• Kent State University
• SPSS Tutorials

Independent Samples t Test

Spss tutorials: independent samples t test.

• The SPSS Environment
• The Data View Window
• Using SPSS Syntax
• Data Creation in SPSS
• Importing Data into SPSS
• Variable Types
• Date-Time Variables in SPSS
• Defining Variables
• Creating a Codebook
• Computing Variables
• Computing Variables: Mean Centering
• Computing Variables: Recoding Categorical Variables
• Computing Variables: Recoding String Variables into Coded Categories (Automatic Recode)
• rank transform converts a set of data values by ordering them from smallest to largest, and then assigning a rank to each value. In SPSS, the Rank Cases procedure can be used to compute the rank transform of a variable." href="https://libguides.library.kent.edu/SPSS/RankCases" style="" >Computing Variables: Rank Transforms (Rank Cases)
• Weighting Cases
• Sorting Data
• Grouping Data
• Descriptive Stats for One Numeric Variable (Explore)
• Descriptive Stats for One Numeric Variable (Frequencies)
• Descriptive Stats for Many Numeric Variables (Descriptives)
• Descriptive Stats by Group (Compare Means)
• Frequency Tables
• Working with "Check All That Apply" Survey Data (Multiple Response Sets)
• Chi-Square Test of Independence
• Pearson Correlation
• One Sample t Test
• Paired Samples t Test
• One-Way ANOVA
• How to Cite the Tutorials

Sample Data Files

Our tutorials reference a dataset called "sample" in many examples. If you'd like to download the sample dataset to work through the examples, choose one of the files below:

• Data definitions (*.pdf)
• Data - Comma delimited (*.csv)
• Data - Tab delimited (*.txt)
• Data - Excel format (*.xlsx)
• Data - SAS format (*.sas7bdat)
• Data - SPSS format (*.sav)

The Independent Samples t Test compares the means of two independent groups in order to determine whether there is statistical evidence that the associated population means are significantly different. The Independent Samples t Test is a parametric test.

This test is also known as:

• Independent t Test
• Independent Measures t Test
• Independent Two-sample t Test
• Student t Test
• Two-Sample t Test
• Uncorrelated Scores t Test
• Unpaired t Test
• Unrelated t Test

The variables used in this test are known as:

• Dependent variable, or test variable
• Independent variable, or grouping variable

Common Uses

The Independent Samples t Test is commonly used to test the following:

• Statistical differences between the means of two groups
• Statistical differences between the means of two interventions
• Statistical differences between the means of two change scores

Note:  The Independent Samples  t  Test can only compare the means for two (and only two) groups. It cannot make comparisons among more than two groups. If you wish to compare the means across more than two groups, you will likely want to run an ANOVA.

Data Requirements

Your data must meet the following requirements:

• Dependent variable that is continuous (i.e., interval or ratio level)
• Independent variable that is categorical (i.e., nominal or ordinal) and has exactly two categories
• Cases that have nonmissing values for both the dependent and independent variables
• Subjects in the first group cannot also be in the second group
• No subject in either group can influence subjects in the other group
• No group can influence the other group
• Violation of this assumption will yield an inaccurate p value
• Random sample of data from the population
• Non-normal population distributions, especially those that are thick-tailed or heavily skewed, considerably reduce the power of the test
• Among moderate or large samples, a violation of normality may still yield accurate p values
• When this assumption is violated and the sample sizes for each group differ, the p value is not trustworthy. However, the Independent Samples t Test output also includes an approximate t statistic that is not based on assuming equal population variances. This alternative statistic, called the Welch t Test statistic 1 , may be used when equal variances among populations cannot be assumed. The Welch t Test is also known an Unequal Variance t Test or Separate Variances t Test.
• No outliers

Note: When one or more of the assumptions for the Independent Samples t Test are not met, you may want to run the nonparametric Mann-Whitney U Test instead.

Researchers often follow several rules of thumb:

• Each group should have at least 6 subjects, ideally more. Inferences for the population will be more tenuous with too few subjects.
• A balanced design (i.e., same number of subjects in each group) is ideal. Extremely unbalanced designs increase the possibility that violating any of the requirements/assumptions will threaten the validity of the Independent Samples t Test.

1  Welch, B. L. (1947). The generalization of "Student's" problem when several different population variances are involved. Biometrika , 34 (1–2), 28–35.

The null hypothesis ( H 0 ) and alternative hypothesis ( H 1 ) of the Independent Samples t Test can be expressed in two different but equivalent ways:

H 0 : µ 1  = µ 2 ("the two population means are equal") H 1 : µ 1  ≠ µ 2 ("the two population means are not equal")

H 0 : µ 1  - µ 2  = 0 ("the difference between the two population means is equal to 0") H 1 :  µ 1  - µ 2  ≠ 0 ("the difference between the two population means is not 0")

where µ 1 and µ 2 are the population means for group 1 and group 2, respectively. Notice that the second set of hypotheses can be derived from the first set by simply subtracting µ 2 from both sides of the equation.

Levene’s Test for Equality of Variances

Recall that the Independent Samples t Test requires the assumption of homogeneity of variance -- i.e., both groups have the same variance. SPSS conveniently includes a test for the homogeneity of variance, called Levene's Test , whenever you run an independent samples t test.

The hypotheses for Levene’s test are: 

H 0 : σ 1 2 - σ 2 2 = 0 ("the population variances of group 1 and 2 are equal") H 1 : σ 1 2 - σ 2 2 ≠ 0 ("the population variances of group 1 and 2 are not equal")

This implies that if we reject the null hypothesis of Levene's Test, it suggests that the variances of the two groups are not equal; i.e., that the homogeneity of variances assumption is violated.

The output in the Independent Samples Test table includes two rows: Equal variances assumed and Equal variances not assumed . If Levene’s test indicates that the variances are equal across the two groups (i.e., p -value large), you will rely on the first row of output, Equal variances assumed , when you look at the results for the actual Independent Samples t Test (under the heading t -test for Equality of Means). If Levene’s test indicates that the variances are not equal across the two groups (i.e., p -value small), you will need to rely on the second row of output, Equal variances not assumed , when you look at the results of the Independent Samples t Test (under the heading t -test for Equality of Means). 

The difference between these two rows of output lies in the way the independent samples t test statistic is calculated. When equal variances are assumed, the calculation uses pooled variances; when equal variances cannot be assumed, the calculation utilizes un-pooled variances and a correction to the degrees of freedom.

Test Statistic

The test statistic for an Independent Samples t Test is denoted t . There are actually two forms of the test statistic for this test, depending on whether or not equal variances are assumed. SPSS produces both forms of the test, so both forms of the test are described here. Note that the null and alternative hypotheses are identical for both forms of the test statistic.

Equal variances assumed

When the two independent samples are assumed to be drawn from populations with identical population variances (i.e., σ 1 2 = σ 2 2 ) , the test statistic t is computed as:

$$ t = \frac{\overline{x}_{1} - \overline{x}_{2}}{s_{p}\sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}} $$

$$ s_{p} = \sqrt{\frac{(n_{1} - 1)s_{1}^{2} + (n_{2} - 1)s_{2}^{2}}{n_{1} + n_{2} - 2}} $$

\(\bar{x}_{1}\) = Mean of first sample \(\bar{x}_{2}\) = Mean of second sample \(n_{1}\) = Sample size (i.e., number of observations) of first sample \(n_{2}\) = Sample size (i.e., number of observations) of second sample \(s_{1}\) = Standard deviation of first sample \(s_{2}\) = Standard deviation of second sample \(s_{p}\) = Pooled standard deviation

The calculated t value is then compared to the critical t value from the t distribution table with degrees of freedom df = n 1 + n 2 - 2 and chosen confidence level. If the calculated t value is greater than the critical t value, then we reject the null hypothesis.

Note that this form of the independent samples t test statistic assumes equal variances.

Because we assume equal population variances, it is OK to "pool" the sample variances ( s p ). However, if this assumption is violated, the pooled variance estimate may not be accurate, which would affect the accuracy of our test statistic (and hence, the p-value).

Equal variances not assumed

When the two independent samples are assumed to be drawn from populations with unequal variances (i.e., σ 1 2  ≠ σ 2 2 ), the test statistic t is computed as:

$$ t = \frac{\overline{x}_{1} - \overline{x}_{2}}{\sqrt{\frac{s_{1}^{2}}{n_{1}} + \frac{s_{2}^{2}}{n_{2}}}} $$

\(\bar{x}_{1}\) = Mean of first sample \(\bar{x}_{2}\) = Mean of second sample \(n_{1}\) = Sample size (i.e., number of observations) of first sample \(n_{2}\) = Sample size (i.e., number of observations) of second sample \(s_{1}\) = Standard deviation of first sample \(s_{2}\) = Standard deviation of second sample

The calculated t value is then compared to the critical t value from the t distribution table with degrees of freedom

$$ df = \frac{ \left ( \frac{s_{1}^2}{n_{1}} + \frac{s_{2}^2}{n_{2}} \right ) ^{2} }{ \frac{1}{n_{1}-1} \left ( \frac{s_{1}^2}{n_{1}} \right ) ^{2} + \frac{1}{n_{2}-1} \left ( \frac{s_{2}^2}{n_{2}} \right ) ^{2}} $$

and chosen confidence level. If the calculated t value > critical t value, then we reject the null hypothesis.

Note that this form of the independent samples t test statistic does not assume equal variances. This is why both the denominator of the test statistic and the degrees of freedom of the critical value of  t are different than the equal variances form of the test statistic.

Data Set-Up

Your data should include two variables (represented in columns) that will be used in the analysis. The independent variable should be categorical and include exactly two groups. (Note that SPSS restricts categorical indicators to numeric or short string values only.) The dependent variable should be continuous (i.e., interval or ratio). SPSS can only make use of cases that have nonmissing values for the independent and the dependent variables, so if a case has a missing value for either variable, it cannot be included in the test.

The number of rows in the dataset should correspond to the number of subjects in the study. Each row of the dataset should represent a unique subject, person, or unit, and all of the measurements taken on that person or unit should appear in that row.

Run an Independent Samples t Test

To run an Independent Samples t Test in SPSS, click  Analyze > Compare Means > Independent-Samples T Test .

The Independent-Samples T Test window opens where you will specify the variables to be used in the analysis. All of the variables in your dataset appear in the list on the left side. Move variables to the right by selecting them in the list and clicking the blue arrow buttons. You can move a variable(s) to either of two areas: Grouping Variable or Test Variable(s) .

A Test Variable(s): The dependent variable(s). This is the continuous variable whose means will be compared between the two groups. You may run multiple t tests simultaneously by selecting more than one test variable.

B Grouping Variable: The independent variable. The categories (or groups) of the independent variable will define which samples will be compared in the t test. The grouping variable must have at least two categories (groups); it may have more than two categories but a t test can only compare two groups, so you will need to specify which two groups to compare. You can also use a continuous variable by specifying a cut point to create two groups (i.e., values at or above the cut point and values below the cut point).

C Define Groups : Click Define Groups to define the category indicators (groups) to use in the t test. If the button is not active, make sure that you have already moved your independent variable to the right in the Grouping Variable field. You must define the categories of your grouping variable before you can run the Independent Samples t Test procedure.

You will not be able to run the Independent Samples t Test until the levels (or cut points) of the grouping variable have been defined. The OK and Paste buttons will be unclickable until the levels have been defined. You can tell if the levels of the grouping variable have not been defined by looking at the Grouping Variable box: if a variable appears in the box but has two question marks next to it, then the levels are not defined:

D Options: The Options section is where you can set your desired confidence level for the confidence interval for the mean difference, and specify how SPSS should handle missing values.

When finished, click OK to run the Independent Samples t Test, or click Paste to have the syntax corresponding to your specified settings written to an open syntax window. (If you do not have a syntax window open, a new window will open for you.)

Define Groups

Clicking the Define Groups button (C) opens the Define Groups window:

1 Use specified values: If your grouping variable is categorical, select Use specified values . Enter the values for the categories you wish to compare in the Group 1 and Group 2 fields. If your categories are numerically coded, you will enter the numeric codes. If your group variable is string, you will enter the exact text strings representing the two categories. If your grouping variable has more than two categories (e.g., takes on values of 1, 2, 3, 4), you can specify two of the categories to be compared (SPSS will disregard the other categories in this case).

Note that when computing the test statistic, SPSS will subtract the mean of the Group 2 from the mean of Group 1. Changing the order of the subtraction affects the sign of the results, but does not affect the magnitude of the results.

2 Cut point: If your grouping variable is numeric and continuous, you can designate a cut point for dichotomizing the variable. This will separate the cases into two categories based on the cut point. Specifically, for a given cut point x , the new categories will be:

• Group 1: All cases where grouping variable > x
• Group 2: All cases where grouping variable < x

Note that this implies that cases where the grouping variable is equal to the cut point itself will be included in the "greater than or equal to" category. (If you want your cut point to be included in a "less than or equal to" group, then you will need to use Recode into Different Variables or use DO IF syntax to create this grouping variable yourself.) Also note that while you can use cut points on any variable that has a numeric type, it may not make practical sense depending on the actual measurement level of the variable (e.g., nominal categorical variables coded numerically). Additionally, using a dichotomized variable created via a cut point generally reduces the power of the test compared to using a non-dichotomized variable.

Clicking the Options button (D) opens the Options window:

The Confidence Interval Percentage box allows you to specify the confidence level for a confidence interval. Note that this setting does NOT affect the test statistic or p-value or standard error; it only affects the computed upper and lower bounds of the confidence interval. You can enter any value between 1 and 99 in this box (although in practice, it only makes sense to enter numbers between 90 and 99).

The Missing Values section allows you to choose if cases should be excluded "analysis by analysis" (i.e. pairwise deletion) or excluded listwise. This setting is not relevant if you have only specified one dependent variable; it only matters if you are entering more than one dependent (continuous numeric) variable. In that case, excluding "analysis by analysis" will use all nonmissing values for a given variable. If you exclude "listwise", it will only use the cases with nonmissing values for all of the variables entered. Depending on the amount of missing data you have, listwise deletion could greatly reduce your sample size.

Example: Independent samples T test when variances are not equal

Problem statement.

In our sample dataset, students reported their typical time to run a mile, and whether or not they were an athlete. Suppose we want to know if the average time to run a mile is different for athletes versus non-athletes. This involves testing whether the sample means for mile time among athletes and non-athletes in your sample are statistically different (and by extension, inferring whether the means for mile times in the population are significantly different between these two groups). You can use an Independent Samples t Test to compare the mean mile time for athletes and non-athletes.

The hypotheses for this example can be expressed as:

H 0 : µ non-athlete  − µ athlete  = 0 ("the difference of the means is equal to zero") H 1 : µ non-athlete  − µ athlete  ≠ 0 ("the difference of the means is not equal to zero")

where µ athlete and µ non-athlete are the population means for athletes and non-athletes, respectively.

In the sample data, we will use two variables: Athlete and MileMinDur . The variable Athlete has values of either “0” (non-athlete) or "1" (athlete). It will function as the independent variable in this T test. The variable MileMinDur is a numeric duration variable (h:mm:ss), and it will function as the dependent variable. In SPSS, the first few rows of data look like this:

Before the Test

Before running the Independent Samples t Test, it is a good idea to look at descriptive statistics and graphs to get an idea of what to expect. Running Compare Means ( Analyze > Compare Means > Means ) to get descriptive statistics by group tells us that the standard deviation in mile time for non-athletes is about 2 minutes; for athletes, it is about 49 seconds. This corresponds to a variance of 14803 seconds for non-athletes, and a variance of 2447 seconds for athletes 1 . Running the Explore procedure ( Analyze > Descriptives > Explore ) to obtain a comparative boxplot yields the following graph:

If the variances were indeed equal, we would expect the total length of the boxplots to be about the same for both groups. However, from this boxplot, it is clear that the spread of observations for non-athletes is much greater than the spread of observations for athletes. Already, we can estimate that the variances for these two groups are quite different. It should not come as a surprise if we run the Independent Samples t Test and see that Levene's Test is significant.

Additionally, we should also decide on a significance level (typically denoted using the Greek letter alpha, α ) before we perform our hypothesis tests. The significance level is the threshold we use to decide whether a test result is significant. For this example, let's use α = 0.05.

1 When computing the variance of a duration variable (formatted as hh:mm:ss or mm:ss or mm:ss.s), SPSS converts the standard deviation value to seconds before squaring.

Running the Test

To run the Independent Samples t Test:

• Click  Analyze > Compare Means > Independent-Samples T Test .
• Move the variable Athlete to the Grouping Variable field, and move the variable MileMinDur to the Test Variable(s) area. Now Athlete is defined as the independent variable and MileMinDur is defined as the dependent variable.
• Click Define Groups , which opens a new window. Use specified values is selected by default. Since our grouping variable is numerically coded (0 = "Non-athlete", 1 = "Athlete"), type “0” in the first text box, and “1” in the second text box. This indicates that we will compare groups 0 and 1, which correspond to non-athletes and athletes, respectively. Click Continue when finished.
• Click OK to run the Independent Samples t Test. Output for the analysis will display in the Output Viewer window. 

Two sections (boxes) appear in the output: Group Statistics and Independent Samples Test . The first section, Group Statistics , provides basic information about the group comparisons, including the sample size ( n ), mean, standard deviation, and standard error for mile times by group. In this example, there are 166 athletes and 226 non-athletes. The mean mile time for athletes is 6 minutes 51 seconds, and the mean mile time for non-athletes is 9 minutes 6 seconds.

The second section, Independent Samples Test , displays the results most relevant to the Independent Samples t Test. There are two parts that provide different pieces of information: (A) Levene’s Test for Equality of Variances and (B) t-test for Equality of Means.

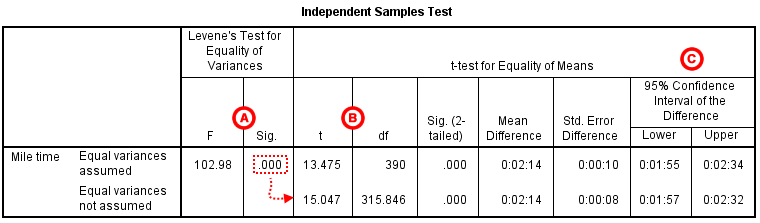
A Levene's Test for Equality of of Variances : This section has the test results for Levene's Test. From left to right:

• F is the test statistic of Levene's test
• Sig. is the p-value corresponding to this test statistic.

The p -value of Levene's test is printed as ".000" (but should be read as p < 0.001 -- i.e., p very small), so we we reject the null of Levene's test and conclude that the variance in mile time of athletes is significantly different than that of non-athletes. This tells us that we should look at the "Equal variances not assumed" row for the t test (and corresponding confidence interval) results . (If this test result had not been significant -- that is, if we had observed p > α -- then we would have used the "Equal variances assumed" output.)

B t-test for Equality of Means provides the results for the actual Independent Samples t Test. From left to right:

• t is the computed test statistic, using the formula for the equal-variances-assumed test statistic (first row of table) or the formula for the equal-variances-not-assumed test statistic (second row of table)
• df is the degrees of freedom, using the equal-variances-assumed degrees of freedom formula (first row of table) or the equal-variances-not-assumed degrees of freedom formula (second row of table)
• Sig (2-tailed) is the p-value corresponding to the given test statistic and degrees of freedom
• Mean Difference is the difference between the sample means, i.e. x 1  − x 2 ; it also corresponds to the numerator of the test statistic for that test
• Std. Error Difference is the standard error of the mean difference estimate; it also corresponds to the denominator of the test statistic for that test

Note that the mean difference is calculated by subtracting the mean of the second group from the mean of the first group. In this example, the mean mile time for athletes was subtracted from the mean mile time for non-athletes (9:06 minus 6:51 = 02:14). The sign of the mean difference corresponds to the sign of the t value. The positive t value in this example indicates that the mean mile time for the first group, non-athletes, is significantly greater than the mean for the second group, athletes.

The associated p value is printed as ".000"; double-clicking on the p-value will reveal the un-rounded number. SPSS rounds p-values to three decimal places, so any p-value too small to round up to .001 will print as .000. (In this particular example, the p-values are on the order of 10 -40 .)

C Confidence Interval of the Difference : This part of the t -test output complements the significance test results. Typically, if the CI for the mean difference contains 0 within the interval -- i.e., if the lower boundary of the CI is a negative number and the upper boundary of the CI is a positive number -- the results are not significant at the chosen significance level. In this example, the 95% CI is [01:57, 02:32], which does not contain zero; this agrees with the small p -value of the significance test.

Decision and Conclusions

Since p < .001 is less than our chosen significance level α = 0.05, we can reject the null hypothesis, and conclude that the that the mean mile time for athletes and non-athletes is significantly different.

Based on the results, we can state the following:

• There was a significant difference in mean mile time between non-athletes and athletes ( t 315.846 = 15.047, p < .001).
• The average mile time for athletes was 2 minutes and 14 seconds lower than the average mile time for non-athletes.
• << Previous: Paired Samples t Test
• Next: One-Way ANOVA >>
• Last Updated: Jul 10, 2024 11:08 AM
• URL: https://libguides.library.kent.edu/SPSS

Street Address

Mailing address, quick links.

• How Are We Doing?
• Student Jobs

Information

• Accessibility
• Emergency Information
• For Our Alumni
• For the Media
• Jobs & Employment
• Life at KSU
• Privacy Statement
• Technology Support
• Website Feedback

• Prompt Library
• DS/AI Trends
• Stats Tools
• Interview Questions
• Generative AI
• Machine Learning
• Deep Learning

Independent Samples T-test: Formula, Examples, Calculator

Last updated: 21st Dec, 2023

As a data scientist , you may often come across scenarios where you need to compare the means of two independent samples . In such cases, a two independent samples t-test , also known as unpaired two samples t-test , is an essential statistical tool that can help you draw meaningful conclusions from your data. This test allows you to determine whether the difference between the means of two independent samples is statistically significant or due to chance.

In this blog, we will cover the concept of independent samples t-test , its formula , real-world examples of its applications and the Python & Excel example (using scipy.stats.ttest_ind function). We will begin with an overview of what an independent samples t-test is, followed by an explanation of two sample t-test formula and related assumptions. Then, we will explore some examples to help you understand how to apply the test in practice. At the end, you also get a calculator for finding out t-statistics and degrees of freedom for independent samples t-test for equal and unequal variance scenarios. Check out other tools on this page – Machine Learning / Statistical Tools .

Table of Contents

What is independent samples or unpaired samples T-test?

The independent samples T-test is defined as statistical hypothesis testing technique in which the samples from two independent groups are compared to determine if the means of the associated populations are significantly different. The t-test compares the means of two groups, such as a control group and a treatment group, to determine if the difference between the groups’ means is statistically significant or due to random chance. For example, lets say that we have two independent groups of marketing professionals having similar qualification and we want to compare their income to determine whether their income is significantly different. 

An independent samples t-test compares the means of two groups. The data are interval for the groups. – Basic and Advanced Statistical Tests

Independent samples t-test is also called unpaired two-samples t-test or just unpaired t-test because the test is performed with only two groups that are independent or unpaired or unrelated. The picture below shows the representation of two independent samples and the aspect of their means. 

The picture below represents represents the need to compare the means of mathematics marks between two independent group (male and female). Independent samples t-test could be performed.

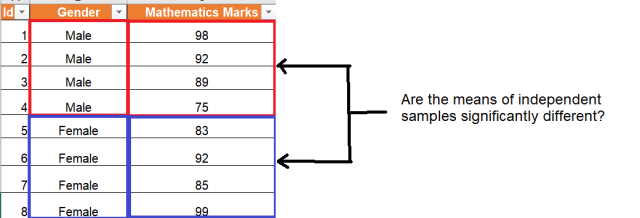
The 2 samples T-test can also be used for pairwise comparisons when the “two” samples represent the same items tested in different scenarios. The pairwise samples t-test will be dealt with in different blog.

Independent Samples T-Test Examples

Let’s say you want to know if two different brands of batteries have the same average life. You could take a battery from each brand, use them until they die, and record the results. This would be an extremely time-consuming process, and it’s not very likely that you’d get a large enough sample size to draw any conclusions. Another option is to use a independent-samples T-test. This test allows you to compare the averages of two groups without having to measure the batteries’ life spans yourself.

The following are a few real-life examples where independent samples T-test  can be used:

• Comparing the sales performance of two products
• Analyzing the effectiveness of two marketing strategies
• Examining the effects of two treatments on patient outcomes
• Comparing the mean blood pressure levels of two patient groups
• Analyzing the differences in academic performance between two schools
• Comparing the mean levels of happiness among two age groups

Independent Samples T-test Assumptions

The following are some assumptions related to independent two sample t-test:

• Assumes that the two samples are independent from each other . The samples in no way should be related to each other.
• The size of sample 30 or less is considered as small sample. That said, the size of the sample is not a strict condition for using T-test.
• Assumes that the two populations have normal distributions . This assumption is crucial, especially when the sample size is small. A normal distribution allows us to use the t-distribution, which is the basis of the t-test.
• Assumes the homogeneity of variance between the two groups. The variance of the data in each sample should be equal. If this assumption is violated, it can lead to biased results. The t-test based on this assumption is also called as homoscedastic t-test    If the assumption of equal variances is violated , an alternative version of the t-test, known as Welch’s t-test (or the Welch’s unequal variances t-test) , should be used. It’s also called as Heteroscedastic t-test. Welch’s t-test does not assume equal variances and is generally more robust to this kind of violation. It adjusts the degrees of freedom used in the t-test to account for the variance differences, providing a more accurate p-value when variances are unequal.
• Assumes that measurements made on the same group of objects are statistically independent of each other.
• Assumes that all observations within each sample are randomly selected and independently distributed. Random sampling helps to ensure that the sample is representative of the population, reducing the likelihood of sampling bias.
• Assumes that there is an equal or nearly equal sample size between the two groups being tested.

Independent Samples T-Test Formula (Lack of Homogeneity of Variances)

The t-statistics formula for independent samples t-test is different based on whether the variance within the two different groups are same / equal or different (statistically). When the variances of populations are not equal , the two samples t-test formula (equation) for t-statistics is following:

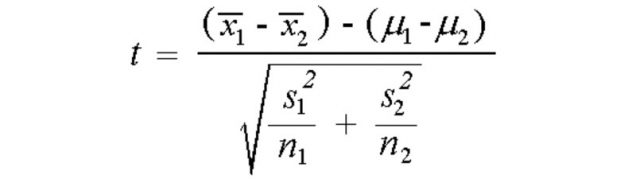
Where X̄1 is mean of first sample, X̄2 is mean of second sample, μ1 is the mean of first population, μ2 is the mean of second population, s1 is the standard deviation of first sample, s2 is the standard deviation of second sample, n1 is the size of the first sample, n2 is the size of the second sample.

The  degrees of freedom formula in two-sample t-test can be calculated as the sum of two sample sizes minus two.

Degrees of freedom , df = n1 + n2 – 2

A confidence interval for the difference between two means specifies a range of values within which the difference between the means of the two populations may lie. The difference between the means of two populations can be estimated based on the following formula:

Difference in population means = Difference in sample means +/- T*standard error

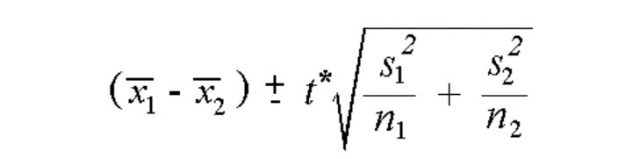
In above formula, the standard error is the square root term.

Independent Two Samples T-test Formula (Equal Population Variances or Standard Deviations)

In case, the two populations’ variances or standard deviations are equal , the formula termed as pooled t-statistics is used based on the usage of pooled standard deviations of the two samples. The following is  pooled t-statistics formula for independent samples t-test:

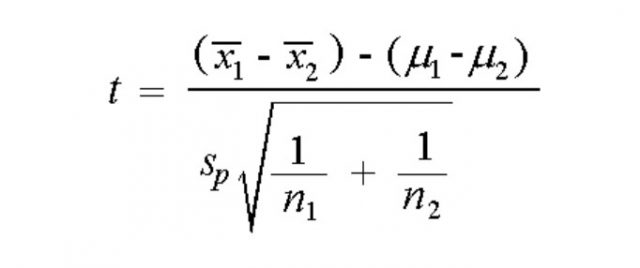
In the above formula, Sp is termed as pooled standard deviation . The formula for pooled variance can be calculated based on the following:

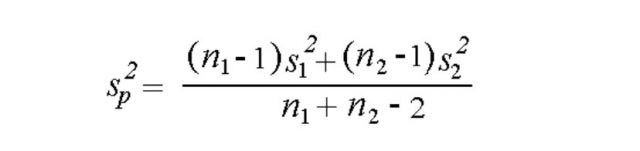
The formula for the degree of freedom in two sample t-test can be calculated as the sum of two sample sizes minus two.

When independent-samples T-test instead of independent-samples Z-test?

Two independent samples t-test and z-test are both statistical tests used to compare the means of two independent samples. However, the choice between the two tests depends on the characteristics of the data and the assumptions that we can make about the population.

In general, a two independent samples z-test is appropriate when we know the population standard deviation and the sample sizes are large. This is because, when sample sizes are large, the sample means are typically normally distributed, and the z-test assumes normality in the population.

On the other hand, a two samples t-test is more appropriate when we do not know the population standard deviation and the sample sizes are small. This is because, when the sample size is small, the sample means may not be normally distributed, and the t-test can provide a more accurate estimate of the population mean. 

Here is the summary of which tests out of z-test or t-test to use in which scenarios:

Two independent samples z-test:

• Large sample size (typically > 30)
• Known population standard deviation
• Normally distributed population

Two independent samples (unpaired) t-test:

• Small sample size (typically < 30)
• Unknown population standard deviation
• Population may not be normally distributed

Independent Samples T-test: T-Statistics Calculation Example

Lets say we need to compare the performance of two call centers in terms of average call lengths and find out if the difference is statistically significant or the difference is a chance occurrence. To start with, we will need to formulate the null and alternate hypothesis. Note that this will be two-tailed T-test as we are performing null hypothesis based on equality of average call length between two call centers.

Null hypothesis, H0 : There is no difference between the average call length between two call centers.

Alternate hypothesis, Ha : There is a difference between the average call length and hence the performance.

We randomly select 20 calls from each call center and calculate the average call lengths. The two call centers seem to have different average call lengths. Is this difference statistically significant?

First, we need to calculate the two sample means and standard deviations:

Call Center A: Sample mean, X̄1 = 122 seconds, SD, S1 = 15 seconds, n1 = 20

Call Center B: Sample mean, X̄2 = 135 seconds, SD, S2 = 20 seconds, n2 = 20

Next, we use a two-sample t-test to determine if the difference between two sample means is statistically significant. We will use a 95% confidence level and α = 0.05.

The two-sample t-statistic is calculated as the following assuming that the standard deviations of the population is not same and the population mean is same.

t = ((135 – 122) – 0)/SQRT((20*20/20) + ((15*15)/20))

t = 13/SQRT(20 + 11.25)

t = 13/SQRT(31.25)

The value of degrees of freedom can be calculated as the following:

Degree of freedom, df = n1 + n2 -2 = 20 + 20 – 2 = 38

The critical value of a two-tailed T-test with degrees of freedom as 38 and level of significance as 0.05 comes out to be 2.0244 . Since the current t-value of 2.3256 is greater than the critical value of 2.0244, one can reject the null hypothesis that there is no difference between the performance in terms of the call length time. Thus, based on the given evidence, the alternate hypothesis stands as true.

Independent Samples T-test: Python Example

The independent (two) samples T-test output can be used to reject null hypothesis or otherwise in two different ways. They are the following:

• Compare the p-value with the level of significance.
• Compare the t-statistics with critical region

Compare the P-Value with Level of Significance

The following represents Python code example for independent samples T-test taking into account the hypothesis discussed in the previous section. The call length observations are, however, different than the previous section. In the code below, the p-value is compared with the level of significance

The following gets printed as an output. Note that the p-value is less than the level of significance, 0.05, and hence the null hypothesis is rejected.

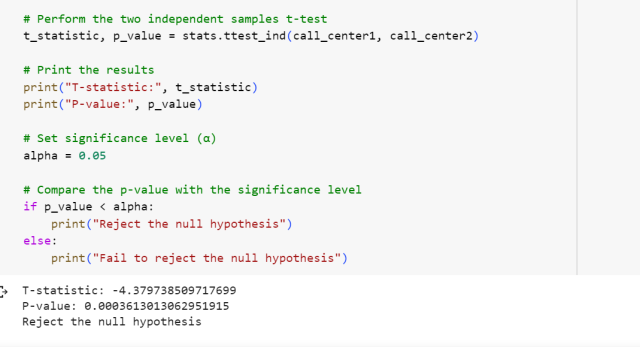
Note some of the following in above Python code example:

• The ttest_ind function from the scipy.stats module was used. This function calculates the t-statistic and the p-value.
• The significance level (α) was set to 0.05, which is a commonly used value.
• The p-value was compared with the significance level .
• If the p-value is less than α (0.05), we print “Reject the null hypothesis,” indicating that there is a significant difference in the average call length between the two call centers.
• If the p-value is greater than or equal to α (0.05), we print “Fail to reject the null hypothesis,” indicating that there is not enough evidence to conclude a significant difference in the average call length between the two call centers.

Compare the T-statistics value with Critical Region Value

The following Python code represents how the output of independent samples T-test can be used to reject the null hypothesis or otherwise by comparing the value of t-statistics and the critical region (threshold).

The output shows like the following. Note that the value of t-statistics (-4.3797) is less than the critical region value (negative of 2.1009 = -2.1009 owing to two-tailed t-test) and hence the null hypothesis will be rejected.

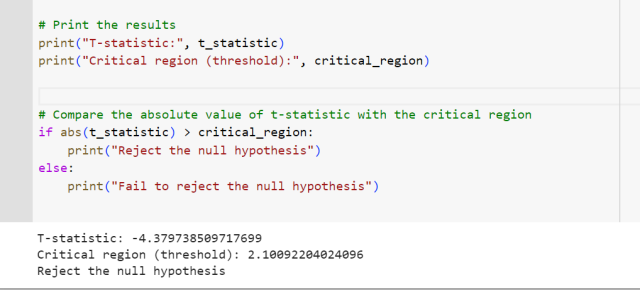
The above can also be understood using the following plot which shows that the value of t-statistics is less than that of the critical region on the negative side and hence, null hypothesis can be rejected,

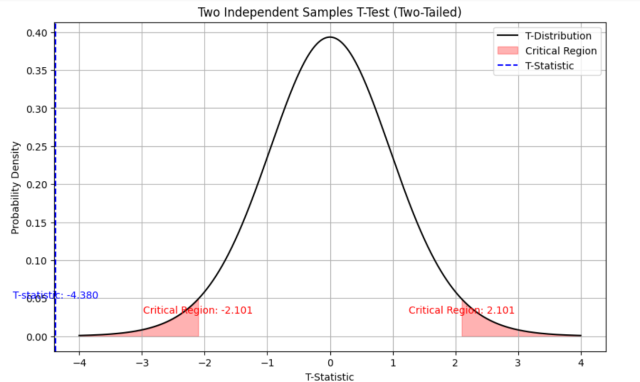
Independent Samples T-Test using Excel: Example

Performing a two-sample t-test in Excel involves a few key steps. I’ll guide you through these using a real-world example. Let’s consider a scenario where we want to compare the mean scores of two different groups, such as test scores from two different classrooms.

Suppose we have the following data for two classes, Xth A and Xth B for Mathematics:

• Classroom Xth A: A set of test scores.
• Classroom Xth B: Another set of test scores.

We want to determine if there is a statistically significant difference in the average scores between the two classrooms. The following steps can be taken:

• Classroom A Scores: e.g., 85, 90, 88, 93, 95
• Classroom B Scores: e.g., 78, 82, 80, 79, 81
• Open a new Excel worksheet.
• Enter the scores for Classroom A in one column (say Column A).
• Enter the scores for Classroom B in the next column (Column B).
• It’s good practice to label your columns. You might put “Classroom A” in cell A1 and “Classroom B” in cell B1.
• You can use Excel functions to do this. For example, in a new cell, write =AVERAGE(A2:A6) for the mean of Classroom A and =STDEV.S(A2:A6) for the standard deviation. Repeat for Classroom B.
• Excel has a built-in function for performing a t-test. You will use the T.TEST function.
• array1 and array2 are the ranges containing your data.
• tails specifies the number of distribution tails. Use 1 for a one-tailed test and 2 for a two-tailed test.
• type is the kind of t-test. Use 1 for paired, 2 for two-sample equal variance (homoscedastic), and 3 for two-sample unequal variance (heteroscedastic). For our example, we would typically use 3.
• The function will return a p-value.
• If the p-value is less than your significance level (commonly 0.05), you can conclude there is a statistically significant difference between the two sets of scores.
• It’s important to properly document your results and methodology for transparency and reproducibility.

Example Calculation

Let’s say your data is in cells A2:A6 for Classroom A and B2:B6 for Classroom B, and you want to perform a two-tailed test assuming unequal variances. We used the value of type as 2 (2 for two-sample equal variance (homoscedastic)). You would enter:

=T.TEST(A2:A6, B2:B6, 2, 2)

The result will be your p-value, which you can use to determine statistical significance.

The following snapshot demonstrates the calculation in an excel spreadsheet.

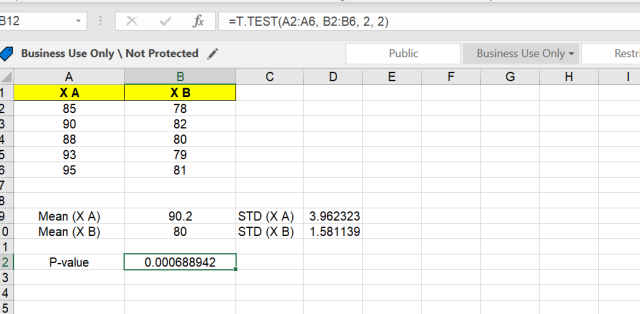
Frequently Asked Questions (FAQs)

Here are few most commonly asked FAQs related to independent samples t-test:

• Two Independent Groups : The core requirement is having two separate, independent groups for comparison. These groups should not overlap or influence each other, such as two different classes of students or patients receiving different treatments.
• Continuous Dependent Variable : The variable you are comparing between the two groups must be continuous. This means it should represent data that can take on a range of values, like heights, weights, or test scores.
• Research Question Focused on Comparing Means : The t-test is specifically designed to compare the means (average values) of the two groups. Your research question should aim to find out if there is a significant difference in these means, such as whether one teaching method results in higher test scores than another.
• Levene’s Test : This is the most widely used method for testing the equality of variances. The null hypothesis for Levene’s Test is that the variances are equal across groups. If the test returns a p-value less than the chosen alpha level (commonly 0.05), you reject the null hypothesis, indicating that the variances are significantly different.
• Visual Inspection (Box Plots, etc.) : Before performing statistical tests, it’s often helpful to visually inspect the data. Box plots can be particularly useful for comparing variances between groups. If the sizes of the boxes (which represent the interquartile range) are notably different, this might suggest a difference in variances.
• The degrees of freedom for a two-sample t-test are calculated based on the sample sizes of the two groups. For a two-sample t-test, the formula for degrees of freedom typically used is: df = n1 + n2 – 2, where n1 is the sample size of the first group and n2 is the sample size of the second group.

Independent Samples T-Test Calculator

Calculate the t-statistics and degrees of freedom for independent samples t-test for equal and unequal variances scenarios .

The two samples t-test for independent samples is a statistical method for comparing two different populations. The t-test can be used when the population standard deviations are not known and the sample size is smaller (less than 30). The two sample t-statistic calculation depends on given degrees of freedom, df = n1 + n2 – 2. If the value of two samples t-test for independent samples exceeds critical T at alpha level, then you can reject null hypothesis that there is no difference between two data sets (H0). Otherwise if two sample T-statistics is less than or equal to critical T at alpha level, then one cannot reject H0; this means both values could have come from same distribution in which case any observed difference would be due to chance alone. Different formulas are required to be used for performing t-test for two independent samples based on whether the variances of two populations are equal or otherwise.

Recent Posts

• Agentic Reasoning Design Patterns in AI: Examples - October 18, 2024
• LLMs for Adaptive Learning & Personalized Education - October 8, 2024
• Sparse Mixture of Experts (MoE) Models: Examples - October 6, 2024

Ajitesh Kumar

2 responses.

How can we cite this article

You can use citation styles as appropriate. Thank you

Kumar, Ajitesh. “Two independent samples t-tests: Formula & Examples.” Vitalflux.com, 22 September 2023, https://www.vitalflux.com/two-independent-samples-t-tests-formula-examples/ .

• Search for:

ChatGPT Prompts (250+)

• Generate Design Ideas for App
• Expand Feature Set of App
• Create a User Journey Map for App
• Generate Visual Design Ideas for App
• Generate a List of Competitors for App
• Agentic Reasoning Design Patterns in AI: Examples
• LLMs for Adaptive Learning & Personalized Education
• Sparse Mixture of Experts (MoE) Models: Examples
• Anxiety Disorder Detection & Machine Learning Techniques
• Confounder Features & Machine Learning Models: Examples

Data Science / AI Trends

• • Sentiment Analysis Real World Examples
• • Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• • Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• • Guides, papers, lecture, notebooks and resources for prompt engineering
• • Common tricks to make LLMs efficient and stable

Free Online Tools

• Create Scatter Plots Online for your Excel Data
• Histogram / Frequency Distribution Creation Tool
• Online Pie Chart Maker Tool
• Z-test vs T-test Decision Tool
• Independent samples t-test calculator

Recent Comments

I found it very helpful. However the differences are not too understandable for me

Very Nice Explaination. Thankyiu very much,

in your case E respresent Member or Oraganization which include on e or more peers?

Such a informative post. Keep it up

Thank you....for your support. you given a good solution for me.

7   Two-sample t-test

Intended learning outcomes.

In this chapter, we will focus on two-sample t-tests, also known as between-groups, between-subjects, or independent-samples t-tests. By the end of this chapter, you should be able to:

• Compute a two-sample t-test and effectively report the results.
• Understand when to use a non-parametric equivalent of the two-sample t-test, compute it, and report the results.

Individual Walkthrough

7.1 activity 1: setup & download the data.

This week, we will be working with a new dataset. Follow the steps below to set up your project:

• Create a new project and name it something meaningful (e.g., “2A_chapter7”, or “07_independent_ttest”). See Section 1.2 if you need some guidance.
• Create a new .Rmd file and save it to your project folder. See Section 1.3 if you get stuck.
• Delete everything after the setup code chunk (e.g., line 12 and below)
• CodebookSimonTask.xlsx: A codebook with detailed variable descriptions
• DemoSimonTask.csv: A CSV file containing demographic information
• MeanSimonTask.csv: A CSV file with the mean response times
• Sup_Mats_Simon_Task.docx: A Word document with Supplementary Materials providing additional details about the task
• RawDataSimonTask.csv: The raw data file, allowing you to explore what experimental data looks like prior to pre-processing.
• Extract the data files from the zip folder and place them in your project folder. If you need help, see Section 1.4 .

Zwaan, R. A., Pecher, D., Paolacci, G., Bouwmeester, S., Verkoeijen, P., Dijkstra, K., & Zeelenberg, R. (2018). Participant nonnaiveté and the reproducibility of cognitive psychology. Psychonomic Bulletin & Review, 25 , 1968-1972. https://doi.org/10.3758/s13423-017-1348-y

The data and supplementary materials are available on OSF: https://osf.io/ghv6m/

Many argue that there is a reproducibility crisis in psychology. We investigated nine well-known effects from the cognitive psychology literature—three each from the domains of perception/action, memory, and language, respectively—and found that they are highly reproducible. Not only can they be reproduced in online environments, but they also can be reproduced with nonnaïve participants with no reduction of effect size. Apparently, some cognitive tasks are so constraining that they encapsulate behavior from external influences, such as testing situation and prior recent experience with the experiment to yield highly robust effects.

Changes made to the dataset

• The dataset, demographic information, and Supplementary Materials have been reduced to include only information related to the Simon Task. The full dataset, which includes the other eight tasks, is available on OSF.
• No other changes were made.

7.2 Activity 2: Library and data for today

Today, we’ll be using the following packages: rstatix , tidyverse , car , lsr , and pwr . You may need to install the packages before using them Make sure that rstatix is loaded in before tidyverse to avoid masking certain functions that we will need later.

We will also read in the data from MeansSimonTask.csv and the demographic information from DemoSimonTask.csv .

7.3 Activity 3: Familiarise yourself with the data

As usual, take some time to familiarise yourself with the data before starting on the between-subjects t-test. Also, more importantly, have a look at the Supplementary Materials in which the Simon effect is explained in more depth.

In general, the Simon effect refers to the phenomenon where participants respond faster when the stimulus appears on the same side of the screen as the button they need to press (i.e., a congruent condition). Conversely, response times are slower when the stimulus appears on the opposite side of the screen from the required button (i.e., an incongruent condition).

In this experiment, all participants completed two sessions of trials. However, they were divided into two groups based on the stimuli they received:

• Same Stimuli Group : Half of the participants received the same set of stimuli in both sessions.
• Different Stimuli Group : The other half received a different set of stimuli in session 2 compared to session 1.

7.3.1 Potential research questions and hypotheses

• Potential research question: “Is there a significant difference in the Simon effect between participants who received the same stimuli in both sessions compared to those who received different stimuli?”
• Null Hypothesis (H 0 ): “There is no significant difference in the Simon effect between participants who received the same stimuli in both sessions and those who received different stimuli.”
• Alternative Hypothesis (H 1 ): “There is a significant difference in the Simon effect between participants who received the same stimuli in both sessions and those who received different stimuli.”

7.4 Activity 4: Preparing the dataframe

The data is already in a very good shape, however, we need to perform some data wrangling to compute the Simon effect.

Steps to calculate the Simon effect:

• For each participant, compute the mean response time (RT) for congruent trials and the mean RT for incongruent trials
• Subtract the mean RT of congruent trials from the mean RT of incongruent trials to calculate the Simon effect

To streamline analysis, we should join this output with the demographics data to have all relevant information in one place.

Basically, we want to create a tibble that has the following content. [Note that I re-arranged the columns and re-labelled some of them in a final step, so your column names and/or order might be slightly different, but content should match.]

Obviously, there are various ways to achieve this, so feel free to explore and come up with your own approach. However, we will provide step-by-step instructions for one of those ways that will get you the desired output.

• Step 1 : Convert the data from wide format to long format, so that all RT values are consolidated into a single column. This transformation will result in each participant having four rows.
• Step 2 : There should be a column now that contained the previous column headings with information on session number and congruency. Separate this information into 2 separate columns (i.e., session number and congruency).
• Step 3 : Compute the mean RT values for each combination of participant , similarity , and congruency
• Step 4 : Pivot the data back to wide format so that the mean RT values for congruent and incongruent trials are placed in two separate columns.
• Step 5 : Add a new column called the simon_effect that calculates the Simon effect by subtracting the mean RT for congruent trials from the mean RT for incongruent trials.
• Step 6 : Merge this processed dataset with the demographics data to ensure all relevant information is in one table.
• Step 7 : Feel free to rearrange the order of columns and/or rename them to match your output with ours (not strictly necessary tbh)

7.5 Activity 5: Compute descriptives

Next, we want to compute number of participants ( n ), means and standard deviations for each group (i.e., same and different ) of our variable of interest (i.e., simon_effect ).

7.6 Activity 6: Create an appropriate plot

Which plot would you choose to represent the data appropriately? Create a plot that effectively visualises the data, and then compare it with the solution provided below.

7.7 Activity 7: Check assumptions

Assumption 1: continuous dv.

The dependent variable must be measured at interval or ratio level. We can confirm that by looking at simon_effect .

Assumption 2: Data are independent

There should be no relationship between the observations. Scores in one condition or observation should not influence scores in another. We assume this assumption holds for our data.

Assumption 3: Homoscedasticity (homogeneity of variance)

This assumption requires the variances between the two groups to be similar (i.e., homoscedasticity). If the variances between the 2 groups are dissimilar/unequal, we have heteroscedasticity.

We can test this using a Levene’s Test for Equality of Variance which is available in the package car . The first argument specifies the formula in the format DV ~ IV . Here:

• The dependent variable (DV) is simon_effect (continuous)
• The independent variable (IV) is similarity (the grouping variable)

To perform the test, separate the variables with a tilde ( ~ ), and specify the dataset using the data argument:

The warning message tells us that the grouping variable was converted into a factor. Oops, I guess we forgot to convert similarity into a factor during data wrangling.

The test output shows a p-value greater than .05 . This indicates that we do not have enough evidence to reject the null hypothesis. Therefore, the variances across the two groups can be assumed equal.

You would report this result in APA style: A Levene’s test of homogeneity of variances was used to compare the variances of the same and the different groups. The test indicated that the variances were homogeneous, \(F(1,158) = 0.73, p = .395\) .

The t-test we are conducting is a Welch t-test by default. The Welch t-test provides similar results to a Student’s t-test when variances are equal but is preferred when variances are unequal.

This means that even if Levene’s test returns a significant p-value, indicating that the variances between the groups are unequal, the Welch t-test remains appropriate and valid for analysis.

Assumption 4: DV should be approximately normally distributed

It’s important to note that this assumption requires the dependent variable to be normally distributed within each group .

We can either use our eyeballs again on the violin-boxplot we created earlier (or use a qqplot, density plot, or histogram instead), OR compute a statistic like the Shapiro-Wilk’s test we already mentioned previously for the one-sample t-test. However, keep in mind that with large sample sizes (approximately 80 participants per group), this test may flag minor deviations from normality as significant, even if the data is reasonably normal.

Visual inspection suggests that both groups are approximately normally distributed. The “same” group appears slightly more normally distributed than the “different” group , which has a small peak in the lower tail. Despite this, both distributions seem normal enough for practical purposes with real-world data.

If you want to use a histogram, density plot or qqplot (the ones created with the ggplot2 and qqplotr packages), you can simply add a facet_wrap() function to display the plots separately for each group.

If you are using the Q-Q plot function from the car package, you will need to create separate data objects filtered for each group before generating Q-Q plots for the groups individually.

As mentioned above, the function for the Shapiro-Wilk’s test does not allow for a formula. This means you will need to create separate data objects for the two groups first. Consider this a good opportunity to practice using the filter() function.

Step-by-step instructions :

• Create separate data objects for the same and different groups.
• Run the Shapiro-Wilk test on each group’s data.
• Examine the results. What do you conclude from the test outcomes?

Interpretation:

Shapiro-Wilk’s test also suggests that the data for both groups, “same” and “different”, are normally distributed as all p-values are above .05.

Again, if you used this method in your report, you would have to write up the results in APA style (refer to the section on the one-sample t-test for guidance on reporting).

If you have read the Delacre et al. (2017) paper ( https://rips-irsp.com/articles/10.5334/irsp.82 ), you might be aware that the normality assumption is not critical for the Welch t-test .

This means that, whether you consider both groups to be “normally distributed” or interpret one as slightly deviating from normality, the Welch t-test remains an appropriate choice for this dataset.

After verifying all the assumptions, we concluded that they were met. Therefore, we will compute a Welch two-sample t-test .

7.8 Activity 8: Compute a Two-sample t-test and effect size

The t.test() function, which we previously used for the one-sample t-test, can also be used here, but with a slightly different approach. It supports a formula option, which simplifies the process. This means we don’t need to wrangle the data further or use the $ operator to access columns directly. Instead, we can specify the formula as DV ~ IV .

The key arguments for t.test() are:

• The first argument in the formula with the pattern DV ~ IV
• The second argument is the data
• The third argument is specifying whether variances are equal between the groups. The default value is var.equal = FALSE , which conducts a Welch t-test . If you set var.equal = TRUE , you would conduct a Student t-test instead.
• The 4th argument alternative specifies the alternative hypothesis. The default value is “two.sided”, meaning the test will check for differences in both directions (i.e., a non-directional hypothesis)

The output of the t.test() function tells us:

• the type of test that was conducted (here Welch t-test)
• the variables that were tested (here simon_effect by similarity ),
• the t-value , degrees of freedom , and p ,
• the alternative hypothesis tested,
• a 95% confidence interval for the difference between group means, and
• the mean of both groups (which should match our descriptive stats)

The t.test() function does not calculate an effect size , so we have to compute it separately once again. As with the one-sample t-test, we can use the CohensD() function from the lsr package. The formula-based approach works here too. For the Welch version of the t-test, you need to include the argument method = "unequal" in the CohensD() function to account for unequal variances.

7.9 Activity 9: Sensitivity power analysis

Next, we will conduct a sensitivity power analysis to determine the minimum effect size that could have been reliably detected with our sample size, an alpha level of 0.05, and a power of 0.8.

To perform this analysis, we use the pwr.t.test() from the pwr package. The arguments are the same as those used for the one-sample t-test, but with a few adjustments:

• Number of Participants : Specify the number of observations per sample (i.e., n)
• Test Type : Set the type argument to “two.sample” for a two-sample t-test.

Sooo, the smallest effect size we can detect with a sample size of 80 participants in each group, an alpha level of .05, and power of .8 is 0.45 . This is larger than the actual effect size we calculated using the CohensD() function (i.e., 0.14). This indicates that our analysis is underpowered to detect such a small effect size.

Hypothetical Replication Study

Out of curiosity, if we were to replicate this study and wanted to reliably detect an effect size as small as 0.14 , how many participants would we need?

We can use the pwr.t.test() function again. This time, instead of specifying n , we provide the effect size ( d = 0.14 ). The result shows that we would need approximately 1,500 participants in total (750 per group). Ooft; that’s quite a few people to recruit.

However, it’s worth noting that an effect size of 0.14 may not be practically meaningful, even if statistically detectable.

No problem! You can use the pwr.t2n.test() function, which allows you to specify different sample sizes for the two groups ( n1 and n2 ).

The rest of the arguments are essentially the same as with pwr.t.test() . Additionally, there is no need to specify the type argument, as the function is specifically designed for two-sample t-tests with unequal sample sizes.

Let’s try it for our example. We should get the same result though.

7.10 Activity 10: The write-up

We hypothesised that there would be a significant difference in the Simon effect between participants who received the same stimuli in both sessions \((N = 80, M = 35.99 msec, SD = 22.40 msec)\) and those who received different stimuli \((N = 80, M = 32.86 msec, SD = 20.79 msec)\) . Using a Welch two-sample t-test, the effect was found to be non-significant and of a small magnitude, \(t(157.14) = 0.92, p = .360, d = 0.15\) . The overall mean difference between groups was small \((M_{diff} = 3.14 msec)\) . Therefore, we fail to reject the null hypothesis.

7.11 Activity 11: Non-parametric alternative

The Mann-Whitney U-test is the non-parametric equivalent of the independent two-sample t-test. It is used to compare the medians of two samples and is particularly useful when the assumptions of the t-test are not met.

According to Delacre et al. (2017), the Mann-Whitney U-test is robust to violations of normality but remains sensitive to heteroscedasticity. In this case, we don’t need to worry about heteroscedasticity, as the variances in the two groups are equal. However, it’s important to keep this in mind when assessing assumptions and interpreting results with other datasets.

First, let’s start by computing some summary statistics for each group.

To conduct a Mann-Whitney U-test , use the wilcox.test() function. As with the independent t-test, you can use the formula approach DV ~ IV . The code structure is identical to what we used for the independent t-test.

We should compute the standardised test statistic Z manually. To do this, use the qnorm() function on the halved p-value obtained from the Wilcoxon test conducted earlier.

The effect size for the Mann-Whitney U-test is r . To compute r, we’d need the standardised test statistic z and divide that the square-root of the number of pairs n: \(r = \frac{|z|}{\sqrt n}\) .

Alternatively, you can use the wilcox_effsize() function from the rstatix package to simplify the process.

The arguments for this function are slightly different in order but otherwise identical to those used in the wilcox.test() function above.

This is once again considered a small effect. Anyway, we do have all the numbers now to write up the results :

A Mann-Whitney U-test was conducted to determine whether there was a significant difference in the Simon effect between participants who received the same stimuli in both sessions \((N = 80, Mdn = 35.68 \text{msec})\) and those who received different stimuli \((N = 80, Mdn = 34.44 \text{msec})\) . The results indicate that the median difference in response time was non-significant and of small magnitude, \(W = 3001, Z = -0.68, p = .498, r = .054\) . Therefore, we fail to reject the null hypothesis.

Pair-coding

Task 1: open the r project for the lab, task 2: create a new .rmd file.

… and name it something useful. If you need help, have a look at Section 1.3 .

Task 3: Load in the library and read in the data

The data should already be in your project folder. If you want a fresh copy, you can download the data again here: data_pair_coding .

We are using the packages tidyverse , car , and lsr today, and the data file we need to read in is dog_data_clean_wide.csv . I’ve named my data object dog_data_wide to shorten the name but feel free to use whatever object name sounds intuitive to you.

If you have not worked through chapter 7 yet, you may need to install a few packages first before you can load them into the library, for example, if car is missing, run install.packages("car") in your CONSOLE .

Task 4: Tidy data for a two-sample t-test

For today’s task, we want to analyse how students’ psychological well-being scores differed at the post_intervention time point. Specifically, we will compare the scores of students who directly interacted with the dogs (Group direct )to those who only talked to the dog handlers (Group control ).

To achieve that, we need to select all relevant columns from dog_data_wide , and narrow down the dataframe to only include students assigned either to the direct or the control groups.

Step 1 : Select all relevant columns from dog_data_wide . For the task at hand, those would be the participant ID RID , GroupAssignment , and Flourishing_post . Store this data in an object called dog_independent .

Step 2 : Narrow down dog_independent to only include GroupAssignment groups direct or the control .

Step 3 : Convert GroupAssignment into a factor.

Task 5: Compute descriptives

Calculate the sample size (n), the mean, and the standard deviation of the psychological well-being score for both groups. Save the output in an object called dog_independent_descriptives . The resulting dataframe should look like this:

Task 6: Check assumptions

Each observation in the dataset has to be independent, meaning the value of one observation does not affect the value of any other. Answer: yes no

I’ve computed Levene’s test below. How do you interpret the output?

Looking at the violin-boxplot below, are both groups normally distributed?

Conclusion from assumption tests

With all assumptions tested, which statistical test would you recommend for this analysis?

Task 7: Computing a two-sample t-test with effect size & interpret the output

• Step 1 : Compute the Welch two-sample t-test. The structure of the function is as follows:
• Step 2 : Calculate an effect size

Calculate Cohen’s D. The structure of the function is as follows:

• Step 3 : Interpreting the output

Below are the outputs for the descriptive statistics (table), Welch t-test (main output), and Cohen’s D (last line starting with [1]). Based on these, write up the results in APA style and provide an interpretation.

The Welch two-sample t-test revealed that there is a statistically significant difference no statistically significant difference in psychological well-being scores between direct (N = , M = , SD = ) and control group (N = , M = , SD = ), t( ) = , p = , V = . The strength of the association between the variables is considered small moderate strong . We therefore fail to reject the null hypothesis reject the null hypothesis .

Test your knowledge

What is the main purpose of an independent t-test?

The independent t-test is specifically designed to compare the means of two separate (independent) groups to determine whether the difference between their means is statistically significant. For example, it could be used to compare the test scores of students who received two different teaching methods (Group 1 vs. Group 2).

Which of the following is a key assumption of the two-sample t-test that should be considered?

Independence of observations is a crucial assumption for the two-sample t-test. It means that the data collected from one participant should not influence the data from another participant.

How can you recognise the difference between the output of a Student’s t-test and a Welch t-test?

The Welch t-test adjusts for unequal variances and sample sizes, which leads to non-integer degrees of freedom. In contrast, the Student’s t-test assumes equal variances and reports integer degrees of freedom based on total sample size minus the number of groups.

The other options are incorrect:

• Both tests report confidence intervals for the mean difference.
• Both tests compare means, not medians.
• Neither test reports effect size directly; it must be calculated separately (e.g., using Cohen’s d).

You perform an independent t-test and find \(t(48)=2.10,p=.042,d=0.58\) . How would you interpret these results?

The p-value ( \(p=.042\) ) is less than the common significance threshold of 0.05, indicating that the difference between the two groups is statistically significant. This means we reject the null hypothesis and conclude that there is evidence of a difference between the group means.