problem solving definition for students

Problem-Solving

Jabberwocky

Problem-solving is the ability to identify and solve problems by applying appropriate skills systematically.

Problem-solving is a process—an ongoing activity in which we take what we know to discover what we don't know. It involves overcoming obstacles by generating hypo-theses, testing those predictions, and arriving at satisfactory solutions.

Problem-solving involves three basic functions:

Seeking information

Generating new knowledge

Making decisions

Problem-solving is, and should be, a very real part of the curriculum. It presupposes that students can take on some of the responsibility for their own learning and can take personal action to solve problems, resolve conflicts, discuss alternatives, and focus on thinking as a vital element of the curriculum. It provides students with opportunities to use their newly acquired knowledge in meaningful, real-life activities and assists them in working at higher levels of thinking (see Levels of Questions ).

Here is a five-stage model that most students can easily memorize and put into action and which has direct applications to many areas of the curriculum as well as everyday life:

Expert Opinion

Here are some techniques that will help students understand the nature of a problem and the conditions that surround it:

• List all related relevant facts.
• Make a list of all the given information.
• Restate the problem in their own words.
• List the conditions that surround a problem.
• Describe related known problems.

It's Elementary

For younger students, illustrations are helpful in organizing data, manipulating information, and outlining the limits of a problem and its possible solution(s). Students can use drawings to help them look at a problem from many different perspectives.

Understand the problem. It's important that students understand the nature of a problem and its related goals. Encourage students to frame a problem in their own words.

Describe any barriers. Students need to be aware of any barriers or constraints that may be preventing them from achieving their goal. In short, what is creating the problem? Encouraging students to verbalize these impediments is always an important step.

Identify various solutions. After the nature and parameters of a problem are understood, students will need to select one or more appropriate strategies to help resolve the problem. Students need to understand that they have many strategies available to them and that no single strategy will work for all problems. Here are some problem-solving possibilities:

Create visual images. Many problem-solvers find it useful to create “mind pictures” of a problem and its potential solutions prior to working on the problem. Mental imaging allows the problem-solvers to map out many dimensions of a problem and “see” it clearly.

Guesstimate. Give students opportunities to engage in some trial-and-error approaches to problem-solving. It should be understood, however, that this is not a singular approach to problem-solving but rather an attempt to gather some preliminary data.

Create a table. A table is an orderly arrangement of data. When students have opportunities to design and create tables of information, they begin to understand that they can group and organize most data relative to a problem.

Use manipulatives. By moving objects around on a table or desk, students can develop patterns and organize elements of a problem into recognizable and visually satisfying components.

Work backward. It's frequently helpful for students to take the data presented at the end of a problem and use a series of computations to arrive at the data presented at the beginning of the problem.

Look for a pattern. Looking for patterns is an important problem-solving strategy because many problems are similar and fall into predictable patterns. A pattern, by definition, is a regular, systematic repetition and may be numerical, visual, or behavioral.

Create a systematic list. Recording information in list form is a process used quite frequently to map out a plan of attack for defining and solving problems. Encourage students to record their ideas in lists to determine regularities, patterns, or similarities between problem elements.

Try out a solution. When working through a strategy or combination of strategies, it will be important for students to …

Keep accurate and up-to-date records of their thoughts, proceedings, and procedures. Recording the data collected, the predictions made, and the strategies used is an important part of the problem solving process.

Try to work through a selected strategy or combination of strategies until it becomes evident that it's not working, it needs to be modified, or it is yielding inappropriate data. As students become more proficient problem-solvers, they should feel comfortable rejecting potential strategies at any time during their quest for solutions.

Monitor with great care the steps undertaken as part of a solution. Although it might be a natural tendency for students to “rush” through a strategy to arrive at a quick answer, encourage them to carefully assess and monitor their progress.

Feel comfortable putting a problem aside for a period of time and tackling it at a later time. For example, scientists rarely come up with a solution the first time they approach a problem. Students should also feel comfortable letting a problem rest for a while and returning to it later.

Evaluate the results. It's vitally important that students have multiple opportunities to assess their own problem-solving skills and the solutions they generate from using those skills. Frequently, students are overly dependent upon teachers to evaluate their performance in the classroom. The process of self-assessment is not easy, however. It involves risk-taking, self-assurance, and a certain level of independence. But it can be effectively promoted by asking students questions such as “How do you feel about your progress so far?” “Are you satisfied with the results you obtained?” and “Why do you believe this is an appropriate response to the problem?”

Featured High School Resources

LESSON PLANS

Romeo and Juliet Teaching Unit Kit

A complete teaching kit for a full or partial unit on Romeo and Juliet Take your students on a thought-provoking, insig...

National Poetry Month Themed Packet for High School

To celebrate Poetry Month, this resource shares 3 activities that will help high school students to engage with poetry i...

Animal Farm Teaching Unit Kit

Everything you need to teach a full or partial unit on Animal Farm Help your students dive into the modern relevance, m...

Related Resources

TEACHING RESOURCE

Textbooks: Advantages and Disadvantages

Textbooks: Advantages and Disadvantages As a new teacher visiting classrooms, you probably notice that most, if not a...

Using Multiple Intelligences in Testing & Assessment

Using Multiple Intelligences in Testing and Assessment Although Howard Gardner's theory of multiple intelligences (MI) i...

Collaboration Between General and Special Education Teachers

Collaboration Between General and Special Education Teachers by: Suzanne Ripley From: The ERIC DigestsERIC EC Dige...

Lesson Plan Procedures: A Guide for Teachers

Lesson Plan Procedures In this article, we will explain how to properly perform a lesson plan in school by diving dee...

Standards for Good Teaching

Standards for Good Teaching You and I and a couple million other people have all been in schools for a number of years,...

Frequently Asked Questions on Inclusion

From: The ERIC Clearinghouse on Disabilities and Gifted Education  How can inclusive practices be incorporated in ear...

About the author

TeacherVision Staff

Teachervision editorial staff.

The TeacherVision editorial team is comprised of teachers, experts, and content professionals dedicated to bringing you the most accurate and relevant information in the teaching space.

Problem Solving Skills: Meaning, Examples & Techniques

Table of Contents

26 January 2021

Reading Time: 2 minutes

Do your children have trouble solving their Maths homework?

Or, do they struggle to maintain friendships at school?

If your answer is ‘Yes,’ the issue might be related to your child’s problem-solving abilities. Whether your child often forgets his/her lunch at school or is lagging in his/her class, good problem-solving skills can be a major tool to help them manage their lives better.

Children need to learn to solve problems on their own. Whether it is about dealing with academic difficulties or peer issues when children are equipped with necessary problem-solving skills they gain confidence and learn to make healthy decisions for themselves. So let us look at what is problem-solving, its benefits, and how to encourage your child to inculcate problem-solving abilities

Problem-solving skills can be defined as the ability to identify a problem, determine its cause, and figure out all possible solutions to solve the problem.

• Trigonometric Problems

What is problem-solving, then? Problem-solving is the ability to use appropriate methods to tackle unexpected challenges in an organized manner. The ability to solve problems is considered a soft skill, meaning that it’s more of a personality trait than a skill you’ve learned at school, on-the-job, or through technical training. While your natural ability to tackle problems and solve them is something you were born with or began to hone early on, it doesn’t mean that you can’t work on it. This is a skill that can be cultivated and nurtured so you can become better at dealing with problems over time.

Problem Solving Skills: Meaning, Examples & Techniques are mentioned below in the Downloadable PDF. 

Benefits of learning problem-solving skills  

Promotes creative thinking and thinking outside the box.

Improves decision-making abilities.

Builds solid communication skills.

Develop the ability to learn from mistakes and avoid the repetition of mistakes.

Problem Solving as an ability is a life skill desired by everyone, as it is essential to manage our day-to-day lives. Whether you are at home, school, or work, life throws us curve balls at every single step of the way. And how do we resolve those? You guessed it right – Problem Solving.

Strengthening and nurturing problem-solving skills helps children cope with challenges and obstacles as they come. They can face and resolve a wide variety of problems efficiently and effectively without having a breakdown. Nurturing good problem-solving skills develop your child’s independence, allowing them to grow into confident, responsible adults. 

Children enjoy experimenting with a wide variety of situations as they develop their problem-solving skills through trial and error. A child’s action of sprinkling and pouring sand on their hands while playing in the ground, then finally mixing it all to eliminate the stickiness shows how fast their little minds work.

Sometimes children become frustrated when an idea doesn't work according to their expectations, they may even walk away from their project. They often become focused on one particular solution, which may or may not work.

However, they can be encouraged to try other methods of problem-solving when given support by an adult. The adult may give hints or ask questions in ways that help the kids to formulate their solutions. 

Encouraging Problem-Solving Skills in Kids

Practice problem solving through games.

Exposing kids to various riddles, mysteries, and treasure hunts, puzzles, and games not only enhances their critical thinking but is also an excellent bonding experience to create a lifetime of memories.

Create a safe environment for brainstorming

Welcome, all the ideas your child brings up to you. Children learn how to work together to solve a problem collectively when given the freedom and flexibility to come up with their solutions. This bout of encouragement instills in them the confidence to face obstacles bravely.

Invite children to expand their Learning capabilities

 Whenever children experiment with an idea or problem, they test out their solutions in different settings. They apply their teachings to new situations and effectively receive and communicate ideas. They learn the ability to think abstractly and can learn to tackle any obstacle whether it is finding solutions to a math problem or navigating social interactions.

Problem-solving is the act of finding answers and solutions to complicated problems. 

Developing problem-solving skills from an early age helps kids to navigate their life problems, whether academic or social more effectively and avoid mental and emotional turmoil.

Children learn to develop a future-oriented approach and view problems as challenges that can be easily overcome by exploring solutions. 

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular  Online Classes  for academics and skill-development, and their Mental Math App, on both  iOS  and  Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial.

Frequently Asked Questions (FAQs)

How do you teach problem-solving skills.

Model a useful problem-solving method. Problem solving can be difficult and sometimes tedious. ... 1. Teach within a specific context. ... 2. Help students understand the problem. ... 3. Take enough time. ... 4. Ask questions and make suggestions. ... 5. Link errors to misconceptions.

What makes a good problem solver?

Excellent problem solvers build networks and know how to collaborate with other people and teams. They are skilled in bringing people together and sharing knowledge and information. A key skill for great problem solvers is that they are trusted by others.

Center for Teaching

Teaching problem solving.

Print Version

Tips and Techniques

Expert vs. novice problem solvers, communicate.

• Have students  identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
• If students are unable to articulate their concerns, determine where they are having trouble by  asking them to identify the specific concepts or principles associated with the problem.
• In a one-on-one tutoring session, ask the student to  work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
• When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)

Encourage Independence

• Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
• Have students work through problems on their own. Ask directing questions or give helpful suggestions, but  provide only minimal assistance and only when needed to overcome obstacles.
• Don’t fear  group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others

Be sensitive

• Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing  positive reinforcement to let students know when they have mastered a new concept or skill.

Encourage Thoroughness and Patience

• Try to communicate that  the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.

Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills,  a teacher should be aware of principles and strategies of good problem solving in his or her discipline .

The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book  How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes  a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides

Quick Links

• Services for Departments and Schools
• Examples of Online Instructional Modules

Why Every Educator Needs to Teach Problem-Solving Skills

Strong problem-solving skills will help students be more resilient and will increase their academic and career success .

Want to learn more about how to measure and teach students’ higher-order skills, including problem solving, critical thinking, and written communication?

Problem-solving skills are essential in school, careers, and life.

Problem-solving skills are important for every student to master. They help individuals navigate everyday life and find solutions to complex issues and challenges. These skills are especially valuable in the workplace, where employees are often required to solve problems and make decisions quickly and effectively.

Problem-solving skills are also needed for students’ personal growth and development because they help individuals overcome obstacles and achieve their goals. By developing strong problem-solving skills, students can improve their overall quality of life and become more successful in their personal and professional endeavors.

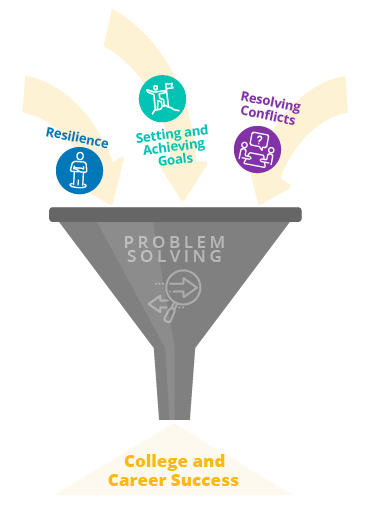
Problem-Solving Skills Help Students…

   develop resilience.

Problem-solving skills are an integral part of resilience and the ability to persevere through challenges and adversity. To effectively work through and solve a problem, students must be able to think critically and creatively. Critical and creative thinking help students approach a problem objectively, analyze its components, and determine different ways to go about finding a solution.  

This process in turn helps students build self-efficacy . When students are able to analyze and solve a problem, this increases their confidence, and they begin to realize the power they have to advocate for themselves and make meaningful change.

When students gain confidence in their ability to work through problems and attain their goals, they also begin to build a growth mindset . According to leading resilience researcher, Carol Dweck, “in a growth mindset, people believe that their most basic abilities can be developed through dedication and hard work—brains and talent are just the starting point. This view creates a love of learning and a resilience that is essential for great accomplishment.”

    Set and Achieve Goals

Students who possess strong problem-solving skills are better equipped to set and achieve their goals. By learning how to identify problems, think critically, and develop solutions, students can become more self-sufficient and confident in their ability to achieve their goals. Additionally, problem-solving skills are used in virtually all fields, disciplines, and career paths, which makes them important for everyone. Building strong problem-solving skills will help students enhance their academic and career performance and become more competitive as they begin to seek full-time employment after graduation or pursue additional education and training.

  Resolve Conflicts

In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes “thinking outside the box” and approaching a conflict by searching for different solutions. This is a very different (and more effective!) method than a more stagnant approach that focuses on placing blame or getting stuck on elements of a situation that can’t be changed.

While it’s natural to get frustrated or feel stuck when working through a conflict, students with strong problem-solving skills will be able to work through these obstacles, think more rationally, and address the situation with a more solution-oriented approach. These skills will be valuable for students in school, their careers, and throughout their lives.

    Achieve Success

We are all faced with problems every day. Problems arise in our personal lives, in school and in our jobs, and in our interactions with others. Employers especially are looking for candidates with strong problem-solving skills. In today’s job market, most jobs require the ability to analyze and effectively resolve complex issues. Students with strong problem-solving skills will stand out from other applicants and will have a more desirable skill set.

In a recent opinion piece published by The Hechinger Report , Virgel Hammonds, Chief Learning Officer at KnowledgeWorks, stated “Our world presents increasingly complex challenges. Education must adapt so that it nurtures problem solvers and critical thinkers.” Yet, the “traditional K–12 education system leaves little room for students to engage in real-world problem-solving scenarios.” This is the reason that a growing number of K–12 school districts and higher education institutions are transforming their instructional approach to personalized and competency-based learning, which encourage students to make decisions, problem solve and think critically as they take ownership of and direct their educational journey.

Problem-Solving Skills Can Be Measured and Taught

Research shows that problem-solving skills can be measured and taught. One effective method is through performance-based assessments which require students to demonstrate or apply their knowledge and higher-order skills to create a response or product or do a task.

What Are Performance-Based Assessments?

With the No Child Left Behind Act (2002), the use of standardized testing became the primary way to measure student learning in the U.S. The legislative requirements of this act shifted the emphasis to standardized testing, and this led to a  decline in nontraditional testing methods .

But   many educators, policy makers, and parents have concerns with standardized tests. Some of the top issues include that they don’t provide feedback on how students can perform better, they don’t value creativity, they are not representative of diverse populations, and they can be disadvantageous to lower-income students.

While standardized tests are still the norm, U.S. Secretary of Education Miguel Cardona is encouraging states and districts to move away from traditional multiple choice and short response tests and instead use performance-based assessment, competency-based assessments, and other more authentic methods of measuring students abilities and skills rather than rote learning. 

Performance-based assessments  measure whether students can apply the skills and knowledge learned from a unit of study. Typically, a performance task challenges students to use their higher-order skills to complete a project or process. Tasks can range from an essay to a complex proposal or design.

Preview a Performance-Based Assessment

Want a closer look at how performance-based assessments work?  Preview CAE’s K–12 and Higher Education assessments and see how CAE’s tools help students develop critical thinking, problem-solving, and written communication skills.

Performance-Based Assessments Help Students Build and Practice Problem-Solving Skills

In addition to effectively measuring students’ higher-order skills, including their problem-solving skills, performance-based assessments can help students practice and build these skills. Through the assessment process, students are given opportunities to practically apply their knowledge in real-world situations. By demonstrating their understanding of a topic, students are required to put what they’ve learned into practice through activities such as presentations, experiments, and simulations. 

This type of problem-solving assessment tool requires students to analyze information and choose how to approach the presented problems. This process enhances their critical thinking skills and creativity, as well as their problem-solving skills. Unlike traditional assessments based on memorization or reciting facts, performance-based assessments focus on the students’ decisions and solutions, and through these tasks students learn to bridge the gap between theory and practice.

Performance-based assessments like CAE’s College and Career Readiness Assessment (CRA+) and Collegiate Learning Assessment (CLA+) provide students with in-depth reports that show them which higher-order skills they are strongest in and which they should continue to develop. This feedback helps students and their teachers plan instruction and supports to deepen their learning and improve their mastery of critical skills.

Explore CAE’s Problem-Solving Assessments

CAE offers performance-based assessments that measure student proficiency in higher-order skills including problem solving, critical thinking, and written communication.

• College and Career Readiness Assessment (CCRA+) for secondary education and
• Collegiate Learning Assessment (CLA+) for higher education.

Our solution also includes instructional materials, practice models, and professional development.

We can help you create a program to build students’ problem-solving skills that includes:

• Measuring students’ problem-solving skills through a performance-based assessment    
• Using the problem-solving assessment data to inform instruction and tailor interventions
• Teaching students problem-solving skills and providing practice opportunities in real-life scenarios
• Supporting educators with quality professional development

Get started with our problem-solving assessment tools to measure and build students’ problem-solving skills today! These skills will be invaluable to students now and in the future.

Ready to Get Started?

Learn more about cae’s suite of products and let’s get started measuring and teaching students important higher-order skills like problem solving..

Problem-Solving in Elementary School

Elementary students practice problem-solving and self-questioning techniques to improve reading and social and emotional learning skills.

Your content has been saved!

In a school district in New Jersey, beginning in kindergarten each child is seen as a future problem solver with creative ideas that can help the world. Vince Caputo, superintendent of the Metuchen School District, explained that what drew him to the position was “a shared value for whole child education.”

Caputo’s first hire as superintendent was Rick Cohen, who works as both the district’s K–12 director of curriculum and principal of Moss Elementary School . Cohen is committed to integrating social and emotional learning (SEL) into academic curriculum and instruction by linking cognitive processes and guided self-talk.

Cohen’s first focus was kindergarten students. “I recommended Moss teachers teach just one problem-solving process to our 6-year-olds across all academic content areas and challenge students to use the same process for social problem-solving,” he explained.  

Reading and Social Problem-Solving

Moss Elementary classrooms use a specific process to develop problem-solving skills focused on tending to social and interpersonal relationships. The process also concentrates on building reading skills—specifically, decoding and comprehension.

Stop, Look, and Think.  Students define the problem. As they read, they look at the pictures and text for clues, searching for information and asking, “What is important and what is not?” Social problem-solving aspect: Students look for signs of feelings in others’ faces, postures, and tone of voice.

Gather Information . Next, students explore what feelings they’re having and what feelings others may be having. As they read, they look at the beginning sound of a word and ask, “What else sounds like this?” Social problem-solving aspect: Students reflect on questions such as, “What word or words describe the feeling you see or hear in others? What word describes your feeling? How do you know, and how sure are you?”

Brainstorming . Then students seek different solutions. As they read, they wonder, “Does it sound right? Does it make sense? How else could it sound to make more sense? What other sounds do those letters make?” Social problem-solving aspect: Students reflect on questions such as, “How can you solve the problem or make the situation better? What else can you think of? What else can you try? What other ideas do you have?”  

Pick the Best One.  Next, students evaluate the solution. While reading, they scan for smaller words they know within larger, more difficult words. They read the difficult words the way they think they sound while asking, “Will it make sense to other people?” Social problem-solving aspect: Students reflect on prompts such as, “Pick the solution that you think will be best to solve the problem. Ask yourself, ‘What will happen if I do this—for me, and for others involved?’”

Go . In the next step, students make a plan and act. They do this by rereading the text. Social problem-solving aspect: Students are asked to try out what they will say and how they will say it. They’re asked to pick a good time to do this, when they’re willing to try it.

Check . Finally, students reflect and revise. After they have read, they ponder what exactly was challenging about what they read and, based on this, decide what to do next. Social problem-solving aspect: Students reflect on questions such as, “How did it work out? Did you solve the problem? How did others feel about what happened? What did you learn? What would you do if the same thing happened again?”

You can watch the Moss Elementary Problem Solvers video and see aspects of this process in action.

The Process of Self-Questioning 

Moss Elementary students and other students in the district are also taught structured self-questioning. Cohen notes, “We realized that many of our elementary students would struggle to generalize the same steps and thinking skills they previously used to figure out an unknown word in a text or resolve social conflicts to think through complex inquiries and research projects.” The solution? Teach students how to self-question, knowing they can also apply this effective strategy across contexts. The self-questioning process students use looks like this:

Stop and Think. “What’s the question?”

Gather Information. “How do I gather information? What are different sides of the issue?”

Brainstorm and Choose. “How do I select, organize, and choose the information? What are some ways to solve the problem? What’s the best choice?”

Plan and Try. “What does the plan look like? When and how can it happen? Who needs to be involved?”

Check & Revise. “How can I present the information? What did I do well? How can I improve?”

The Benefits

Since using the problem-solving and self-questioning processes, the students at Moss Elementary have had growth in their scores for the last two years on the fifth-grade English language arts PARCC tests . However, as Cohen shares, “More important than preparing our students for the tests on state standards, there is evidence that we are also preparing them for the tests of life.”

Don’t Just Tell Students to Solve Problems. Teach Them How.

The positive impact of an innovative UC San Diego problem-solving educational curriculum continues to grow

• Daniel Kane - [email protected]

Published Date

Share this:, article content.

Problem solving is a critical skill for technical education and technical careers of all types. But what are best practices for teaching problem solving to high school and college students? 

The University of California San Diego Jacobs School of Engineering is on the forefront of efforts to improve how problem solving is taught. This UC San Diego approach puts hands-on problem-identification and problem-solving techniques front and center. Over 1,500 students across the San Diego region have already benefited over the last three years from this program. In the 2023-2024 academic year, approximately 1,000 upper-level high school students will be taking the problem solving course in four different school districts in the San Diego region. Based on the positive results with college students, as well as high school juniors and seniors in the San Diego region, the project is getting attention from educators across the state of California, and around the nation and the world.

{/exp:typographee}

In Summer 2023, th e 27 community college students who took the unique problem-solving course developed at the UC San Diego Jacobs School of Engineering thrived, according to Alex Phan PhD, the Executive Director of Student Success at the UC San Diego Jacobs School of Engineering. Phan oversees the project. 

Over the course of three weeks, these students from Southwestern College and San Diego City College poured their enthusiasm into problem solving through hands-on team engineering challenges. The students brimmed with positive energy as they worked together. 

What was noticeably absent from this laboratory classroom: frustration.

“In school, we often tell students to brainstorm, but they don’t often know where to start. This curriculum gives students direct strategies for brainstorming, for identifying problems, for solving problems,” sai d Jennifer Ogo, a teacher from Kearny High School who taught the problem-solving course in summer 2023 at UC San Diego. Ogo was part of group of educators who took the course themselves last summer.

The curriculum has been created, refined and administered over the last three years through a collaboration between the UC San Diego Jacobs School of Engineering and the UC San Diego Division of Extended Studies. The project kicked off in 2020 with a generous gift from a local philanthropist.

Not getting stuck

One of the overarching goals of this project is to teach both problem-identification and problem-solving skills that help students avoid getting stuck during the learning process. Stuck feelings lead to frustration – and when it’s a Science, Technology, Engineering and Math (STEM) project, that frustration can lead students to feel they don’t belong in a STEM major or a STEM career. Instead, the UC San Diego curriculum is designed to give students the tools that lead to reactions like “this class is hard, but I know I can do this!” –  as Ogo, a celebrated high school biomedical sciences and technology teacher, put it. 

Three years into the curriculum development effort, the light-hearted energy of the students combined with their intense focus points to success. On the last day of the class, Mourad Mjahed PhD, Director of the MESA Program at Southwestern College’s School of Mathematics, Science and Engineering came to UC San Diego to see the final project presentations made by his 22 MESA students.

“Industry is looking for students who have learned from their failures and who have worked outside of their comfort zones,” said Mjahed. The UC San Diego problem-solving curriculum, Mjahed noted, is an opportunity for students to build the skills and the confidence to learn from their failures and to work outside their comfort zone. “And from there, they see pathways to real careers,” he said. 

What does it mean to explicitly teach problem solving? 

This approach to teaching problem solving includes a significant focus on learning to identify the problem that actually needs to be solved, in order to avoid solving the wrong problem. The curriculum is organized so that each day is a complete experience. It begins with the teacher introducing the problem-identification or problem-solving strategy of the day. The teacher then presents case studies of that particular strategy in action. Next, the students get introduced to the day’s challenge project. Working in teams, the students compete to win the challenge while integrating the day’s technique. Finally, the class reconvenes to reflect. They discuss what worked and didn't work with their designs as well as how they could have used the day’s problem-identification or problem-solving technique more effectively. 

The challenges are designed to be engaging – and over three years, they have been refined to be even more engaging. But the student engagement is about much more than being entertained. Many of the students recognize early on that the problem-identification and problem-solving skills they are learning can be applied not just in the classroom, but in other classes and in life in general. 

Gabriel from Southwestern College is one of the students who saw benefits outside the classroom almost immediately. In addition to taking the UC San Diego problem-solving course, Gabriel was concurrently enrolled in an online computer science programming class. He said he immediately started applying the UC San Diego problem-identification and troubleshooting strategies to his coding assignments. 

Gabriel noted that he was given a coding-specific troubleshooting strategy in the computer science course, but the more general problem-identification strategies from the UC San Diego class had been extremely helpful. It’s critical to “find the right problem so you can get the right solution. The strategies here,” he said, “they work everywhere.”

Phan echoed this sentiment. “We believe this curriculum can prepare students for the technical workforce. It can prepare students to be impactful for any career path.”

The goal is to be able to offer the course in community colleges for course credit that transfers to the UC, and to possibly offer a version of the course to incoming students at UC San Diego. 

As the team continues to work towards integrating the curriculum in both standardized high school courses such as physics, and incorporating the content as a part of the general education curriculum at UC San Diego, the project is expected to impact thousands more students across San Diego annually. 

Portrait of the Problem-Solving Curriculum

On a sunny Wednesday in July 2023, an experiential-learning classroom was full of San Diego community college students. They were about half-way through the three-week problem-solving course at UC San Diego, held in the campus’ EnVision Arts and Engineering Maker Studio. On this day, the students were challenged to build a contraption that would propel at least six ping pong balls along a kite string spanning the laboratory. The only propulsive force they could rely on was the air shooting out of a party balloon.

A team of three students from Southwestern College – Valeria, Melissa and Alondra – took an early lead in the classroom competition. They were the first to use a plastic bag instead of disposable cups to hold the ping pong balls. Using a bag, their design got more than half-way to the finish line – better than any other team at the time – but there was more work to do. 

As the trio considered what design changes to make next, they returned to the problem-solving theme of the day: unintended consequences. Earlier in the day, all the students had been challenged to consider unintended consequences and ask questions like: When you design to reduce friction, what happens? Do new problems emerge? Did other things improve that you hadn’t anticipated? 

Other groups soon followed Valeria, Melissa and Alondra’s lead and began iterating on their own plastic-bag solutions to the day’s challenge. New unintended consequences popped up everywhere. Switching from cups to a bag, for example, reduced friction but sometimes increased wind drag. 

Over the course of several iterations, Valeria, Melissa and Alondra made their bag smaller, blew their balloon up bigger, and switched to a different kind of tape to get a better connection with the plastic straw that slid along the kite string, carrying the ping pong balls. 

One of the groups on the other side of the room watched the emergence of the plastic-bag solution with great interest. 

“We tried everything, then we saw a team using a bag,” said Alexander, a student from City College. His team adopted the plastic-bag strategy as well, and iterated on it like everyone else. They also chose to blow up their balloon with a hand pump after the balloon was already attached to the bag filled with ping pong balls – which was unique. 

“I don’t want to be trying to put the balloon in place when it's about to explode,” Alexander explained. 

Asked about whether the structured problem solving approaches were useful, Alexander’s teammate Brianna, who is a Southwestern College student, talked about how the problem-solving tools have helped her get over mental blocks. “Sometimes we make the most ridiculous things work,” she said. “It’s a pretty fun class for sure.” 

Yoshadara, a City College student who is the third member of this team, described some of the problem solving techniques this way: “It’s about letting yourself be a little absurd.”

Alexander jumped back into the conversation. “The value is in the abstraction. As students, we learn to look at the problem solving that worked and then abstract out the problem solving strategy that can then be applied to other challenges. That’s what mathematicians do all the time,” he said, adding that he is already thinking about how he can apply the process of looking at unintended consequences to improve both how he plays chess and how he goes about solving math problems.

Looking ahead, the goal is to empower as many students as possible in the San Diego area and  beyond to learn to problem solve more enjoyably. It’s a concrete way to give students tools that could encourage them to thrive in the growing number of technical careers that require sharp problem-solving skills, whether or not they require a four-year degree. 

You May Also Like

Researchers develop clinically validated, wearable ultrasound patch for continuous blood pressure monitoring, uc san diego foundation board of trustees: driving meaningful change, near and far, six solutions against climate change: researchers launch call-action for rapid response to mobilize solutions, on the origin of life: how the first cell membranes came to exist, stay in the know.

Keep up with all the latest from UC San Diego. Subscribe to the newsletter today.

You have been successfully subscribed to the UC San Diego Today Newsletter.

Campus & Community

Arts & culture, visual storytelling.

• Media Resources & Contacts

Publications:

• UC San Diego Today Newsletter
• UC San Diego Magazine
• Discoveries Magazine

Popular Searches: Covid-19   Ukraine   Campus & Community   Arts & Culture   Voices

Chapter 9: Facilitating Complex Thinking

Problem-solving.

Somewhat less open-ended than creative thinking is problem solving , the analysis and solution of tasks or situations that are complex or ambiguous and that pose difficulties or obstacles of some kind (Mayer & Wittrock, 2006). Problem solving is needed, for example, when a physician analyzes a chest X-ray: a photograph of the chest is far from clear and requires skill, experience, and resourcefulness to decide which foggy-looking blobs to ignore, and which to interpret as real physical structures (and therefore real medical concerns). Problem solving is also needed when a grocery store manager has to decide how to improve the sales of a product: should she put it on sale at a lower price, or increase publicity for it, or both? Will these actions actually increase sales enough to pay for their costs?

Example 1: Problem Solving in the Classroom

Problem solving happens in classrooms when teachers present tasks or challenges that are deliberately complex and for which finding a solution is not straightforward or obvious. The responses of students to such problems, as well as the strategies for assisting them, show the key features of problem solving. Consider this example, and students’ responses to it. We have numbered and named the paragraphs to make it easier to comment about them individually:

Scene #1: A problem to be solved

A teacher gave these instructions: “Can you connect all of the dots below using only four straight lines?” She drew the following display on the chalkboard:

The problem itself and the procedure for solving it seemed very clear: simply experiment with different arrangements of four lines. But two volunteers tried doing it at the board, but were unsuccessful. Several others worked at it at their seats, but also without success.

Scene #2: Coaxing students to re-frame the problem

When no one seemed to be getting it, the teacher asked, “Think about how you’ve set up the problem in your mind—about what you believe the problem is about. For instance, have you made any assumptions about how long the lines ought to be? Don’t stay stuck on one approach if it’s not working!”

Scene #3: Alicia abandons a fixed response

After the teacher said this, Alicia indeed continued to think about how she saw the problem. “The lines need to be no longer than the distance across the square,” she said to herself. So she tried several more solutions, but none of them worked either.

The teacher walked by Alicia’s desk and saw what Alicia was doing. She repeated her earlier comment: “Have you assumed anything about how long the lines ought to be?”

Alicia stared at the teacher blankly, but then smiled and said, “Hmm! You didn’t actually say that the lines could be no longer than the matrix! Why not make them longer?” So she experimented again using oversized lines and soon discovered a solution:

Scene #4: Willem’s and Rachel’s alternative strategies

Meanwhile, Willem worked on the problem. As it happened, Willem loved puzzles of all kinds, and had ample experience with them. He had not, however, seen this particular problem. “It must be a trick,” he said to himself, because he knew from experience that problems posed in this way often were not what they first appeared to be. He mused to himself: “Think outside the box, they always tell you. . .” And that was just the hint he needed: he drew lines outside the box by making them longer than the matrix and soon came up with this solution:

When Rachel went to work, she took one look at the problem and knew the answer immediately: she had seen this problem before, though she could not remember where. She had also seen other drawing-related puzzles, and knew that their solution always depended on making the lines longer, shorter, or differently angled than first expected. After staring at the dots briefly, she drew a solution faster than Alicia or even Willem. Her solution looked exactly like Willem’s.

This story illustrates two common features of problem solving: the effect of degree of structure or constraint on problem solving, and the effect of mental obstacles to solving problems. The next sections discuss each of these features, and then looks at common techniques for solving problems.

The effect of constraints: well-structured versus ill-structured problems

Problems vary in how much information they provide for solving a problem, as well as in how many rules or procedures are needed for a solution. A well-structured problem provides much of the information needed and can in principle be solved using relatively few clearly understood rules. Classic examples are the word problems often taught in math lessons or classes: everything you need to know is contained within the stated problem and the solution procedures are relatively clear and precise. An ill-structured problem has the converse qualities: the information is not necessarily within the problem, solution procedures are potentially quite numerous, and a multiple solutions are likely (Voss, 2006). Extreme examples are problems like “How can the world achieve lasting peace?” or “How can teachers insure that students learn?”

By these definitions, the nine-dot problem is relatively well-structured—though not completely. Most of the information needed for a solution is provided in Scene #1: there are nine dots shown and instructions given to draw four lines. But not all necessary information was given: students needed to consider lines that were longer than implied in the original statement of the problem. Students had to “think outside the box,” as Willem said—in this case, literally.

When a problem is well-structured, so are its solution procedures likely to be as well. A well-defined procedure for solving a particular kind of problem is often called an algorithm ; examples are the procedures for multiplying or dividing two numbers or the instructions for using a computer (Leiserson, et al., 2001). Algorithms are only effective when a problem is very well-structured and there is no question about whether the algorithm is an appropriate choice for the problem. In that situation it pretty much guarantees a correct solution. They do not work well, however, with ill-structured problems, where they are ambiguities and questions about how to proceed or even about precisely what the problem is about. In those cases it is more effective to use heuristics , which are general strategies—“rules of thumb,” so to speak—that do not always work, but often do, or that provide at least partial solutions. When beginning research for a term paper, for example, a useful heuristic is to scan the library catalogue for titles that look relevant. There is no guarantee that this strategy will yield the books most needed for the paper, but the strategy works enough of the time to make it worth trying.

In the nine-dot problem, most students began in Scene #1 with a simple algorithm that can be stated like this: “Draw one line, then draw another, and another, and another.” Unfortunately this simple procedure did not produce a solution, so they had to find other strategies for a solution. Three alternatives are described in Scenes #3 (for Alicia) and 4 (for Willem and Rachel). Of these, Willem’s response resembled a heuristic the most: he knew from experience that a good general strategy that often worked for such problems was to suspect a deception or trick in how the problem was originally stated. So he set out to question what the teacher had meant by the word line , and came up with an acceptable solution as a result.

Common obstacles to solving problems

The example also illustrates two common problems that sometimes happen during problem solving. One of these is functional fixedness : a tendency to regard the functions of objects and ideas as fixed (German & Barrett, 2005). Over time, we get so used to one particular purpose for an object that we overlook other uses. We may think of a dictionary, for example, as necessarily something to verify spellings and definitions, but it also can function as a gift, a doorstop, or a footstool. For students working on the nine-dot matrix described in the last section, the notion of “drawing” a line was also initially fixed; they assumed it to be connecting dots but not extending lines beyond the dots. Functional fixedness sometimes is also called response set , the tendency for a person to frame or think about each problem in a series in the same way as the previous problem, even when doing so is not appropriate to later problems. In the example of the nine-dot matrix described above, students often tried one solution after another, but each solution was constrained by a set response not to extend any line beyond the matrix.

Functional fixedness and the response set are obstacles in problem representation , the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely—if indeed the problem can be solved at all. With the nine-dot matrix problem, for example, construing the instruction to draw four lines as meaning “draw four lines entirely within the matrix” means that the problem simply could not be solved. For another, consider this problem: “The number of water lilies on a lake doubles each day. Each water lily covers exactly one square foot. If it takes 100 days for the lilies to cover the lake exactly, how many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is not relevant to the solution, and only serves to distract from the truly crucial information, the fact that the lilies double their coverage each day. (The answer, incidentally, is that the lake is half covered in 99 days; can you think why?)

Strategies to assist problem solving

Just as there are cognitive obstacles to problem solving, there are also general strategies that help the process be successful, regardless of the specific content of a problem (Thagard, 2005). One helpful strategy is problem analysis —identifying the parts of the problem and working on each part separately. Analysis is especially useful when a problem is ill-structured. Consider this problem, for example: “Devise a plan to improve bicycle transportation in the city.” Solving this problem is easier if you identify its parts or component subproblems, such as (1) installing bicycle lanes on busy streets, (2) educating cyclists and motorists to ride safely, (3) fixing potholes on streets used by cyclists, and (4) revising traffic laws that interfere with cycling. Each separate subproblem is more manageable than the original, general problem. The solution of each subproblem contributes the solution of the whole, though of course is not equivalent to a whole solution.

Another helpful strategy is working backward from a final solution to the originally stated problem. This approach is especially helpful when a problem is well-structured but also has elements that are distracting or misleading when approached in a forward, normal direction. The water lily problem described above is a good example: starting with the day when all the lake is covered (Day 100), ask what day would it therefore be half covered (by the terms of the problem, it would have to be the day before, or Day 99). Working backward in this case encourages reframing the extra information in the problem (i. e. the size of each water lily) as merely distracting, not as crucial to a solution.

A third helpful strategy is analogical thinking —using knowledge or experiences with similar features or structures to help solve the problem at hand (Bassok, 2003). In devising a plan to improve bicycling in the city, for example, an analogy of cars with bicycles is helpful in thinking of solutions: improving conditions for both vehicles requires many of the same measures (improving the roadways, educating drivers). Even solving simpler, more basic problems is helped by considering analogies. A first grade student can partially decode unfamiliar printed words by analogy to words he or she has learned already. If the child cannot yet read the word screen , for example, he can note that part of this word looks similar to words he may already know, such as seen or green , and from this observation derive a clue about how to read the word screen . Teachers can assist this process, as you might expect, by suggesting reasonable, helpful analogies for students to consider.

Bassok, J. (2003). Analogical transfer in problem solving. In Davidson, J. & Sternberg, R. (Eds.). The psychology of problem solving. New York: Cambridge University Press.

German, T. & Barrett, H. (2005). Functional fixedness in a technologically sparse culture. Psychological Science, 16 (1), 1–5.

Leiserson, C., Rivest, R., Cormen, T., & Stein, C. (2001). Introduction to algorithms. Cambridge, MA: MIT Press.

Luchins, A. & Luchins, E. (1994). The water-jar experiment and Einstellung effects. Gestalt Theory: An International Interdisciplinary Journal, 16 (2), 101–121.

Mayer, R. & Wittrock, M. (2006). Problem-solving transfer. In D. Berliner & R. Calfee (Eds.), Handbook of Educational Psychology, pp. 47–62. Mahwah, NJ: Erlbaum.

Thagard, R. (2005). Mind: Introduction to Cognitive Science, 2nd edition. Cambridge, MA: MIT Press.

Voss, J. (2006). Toulmin’s model and the solving of ill-structured problems. Argumentation, 19 (3), 321–329.

Candela Citations

• Educational Psychology. Authored by : Kelvin Seifert and Rosemary Sutton. Located at : https://open.umn.edu/opentextbooks/BookDetail.aspx?bookId=153 . License : CC BY: Attribution

Powerful online learning at your pace

What IS Problem-Solving?

Ask teachers about problem-solving strategies, and you’re opening a can of worms! Opinions about the “best” way to teach problem-solving are all over the board. And teachers will usually argue for their process quite passionately.

When I first started teaching math over 25 years ago, it was very common to teach “keywords” to help students determine the operation to use when solving a word problem. For example, if you see the word “total” in the problem, you always add. Rather than help students become better problem solvers, the use of keywords actually resulted in students who don’t even feel the need to read and understand the problem–just look for the keywords, pick out the numbers, and do the operation indicated by the keyword.

This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.

Another common strategy for teaching problem-solving is the use of acrostics that students can easily remember to perform the “steps” in problem-solving. CUBES is an example. Just as with keywords, however, students often follow the steps with little understanding. As an example, a common step is to underline or highlight the question. But if you ask students why they are underlining or highlighting the question, they often can’t tell you. The question is , in fact, super important, but they’ve not been told why. They’ve been told to underline the question, so they do.

The problem with both keywords and the rote-step strategies is that both methods try to turn something that is inherently messy into an algorithm! It’s way past time that we leave both methods behind.

First, we need to broaden the definition of problem-solving. Somewhere along the line, problem-solving became synonymous with “word problems.” In reality, it’s so much more. Every one of us solves dozens or hundreds of problems every single day, and most of us haven’t solved a word problem in years. Problem-solving is often described as  figuring out what to do when you don’t  know what to do.  My power went out unexpectedly this morning, and I have work to do. That’s a problem that I had to solve. I had to think about what the problem was, what my options were, and formulate a plan to solve the problem. No keywords. No acrostics. I’m using my phone as a hotspot and hoping my laptop battery doesn’t run out. Problem solved. For now.

If you want to get back to what problem-solving really is, you should consult the work of George Polya. His book, How to Solve It , which was first published in 1945, outlined four principles for problem-solving. The four principles are: understand the problem, devise a plan, carry out the plan, and look back. This document from UC Berkeley’s Mathematics department is a great 4-page overview of Polya’s process. You can probably see that the keyword and rote-steps strategies were likely based on Polya’s method, but it really got out of hand. We need to help students think , not just follow steps.

I created both primary and intermediate posters based on Polya’s principles. Grab your copies for free here !

I would LOVE to hear your comments about problem-solving!

Similar Posts

Representing Numbers to 120 FREEBIE

I absolutely love workstation activities that are easy to prep, easy for the kiddos to understand and do, are easily differentiated, and grow with the students as their skills develop….

Hundred Chart Boot Camp

  Mathematics is all about patterns. Some describe mathematics as the science of patterns, and the ability to understand patterns is described as a key concept in NCTM‘s algebra standard….

Multiplication Fact Game for Doubles Strategy

A couple of weeks ago I posted a fun Bump game featuring the doubles strategy for learning multiplication facts, and today’s freebie features more practice on that same strategy. Basically,…

Hundred Chart Activities: The 100 House

One of the things that’s awesome about being a math coach is having the opportunity to interact with so many creative teachers on a daily basis! I picked up this…

Humpty Dumpty 120 Chart…Putting the Pieces Together Again

“All the King’s horses and all the King’s men, couldn’t put Humpty together again.” But maybe your kiddos can! This post contains affiliate links, which simply means that when you use my…

Literature Link: Too Much Glue

As you are planning for the fall (I know, some of you are still in school…), I’m sure you’re giving thought to how you will launch your math journals.  As…

Do you tutor teachers?

I do professional development for district and schools, and I have online courses.

You make a great point when you mentioned that teaching students to look for “keywords” is not teaching students to become better problem solvers. I was once guilty of using the CUBES strategy, but have since learned to provide students with opportunity to grapple with solving a problem and not providing them with specified steps to follow.

I think we’ve ALL been there! We learn and we do better. 🙂

Love this article and believe that we can do so much better as math teachers than just teaching key words! Do you have an editable version of this document? We are wanting to use something similar for our school, but would like to tweak it just a bit. Thank you!

I’m sorry, but because of the clip art and fonts I use, I am not able to provide an editable version.

Hi Donna! I am working on my dissertation that focuses on problem-solving. May I use your intermediate poster as a figure, giving credit to you in my citation with your permission, for my section on Polya’s Traditional Problem-Solving Steps? You laid out the process so succinctly with examples that my research could greatly benefit from this image. Thank you in advance!

Absolutely! Good luck with your dissertation!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Skip to main content
• Skip to primary sidebar

IResearchNet

Problem Solving

Problem solving, a fundamental cognitive process deeply rooted in psychology, plays a pivotal role in various aspects of human existence, especially within educational contexts. This article delves into the nature of problem solving, exploring its theoretical underpinnings, the cognitive and psychological processes that underlie it, and the application of problem-solving skills within educational settings and the broader real world. With a focus on both theory and practice, this article underscores the significance of cultivating problem-solving abilities as a cornerstone of cognitive development and innovation, shedding light on its applications in fields ranging from education to clinical psychology and beyond, thereby paving the way for future research and intervention in this critical domain of human cognition.

Introduction

Problem solving, a quintessential cognitive process deeply embedded in the domains of psychology and education, serves as a linchpin for human intellectual development and adaptation to the ever-evolving challenges of the world. The fundamental capacity to identify, analyze, and surmount obstacles is intrinsic to human nature and has been a subject of profound interest for psychologists, educators, and researchers alike. This article aims to provide a comprehensive exploration of problem solving, investigating its theoretical foundations, cognitive intricacies, and practical applications in educational contexts. With a clear understanding of its multifaceted nature, we will elucidate the pivotal role that problem solving plays in enhancing learning, fostering creativity, and promoting cognitive growth, setting the stage for a detailed examination of its significance in both psychology and education. In the continuum of psychological research and educational practice, problem solving stands as a cornerstone, enabling individuals to navigate the complexities of their world. This article’s thesis asserts that problem solving is not merely a cognitive skill but a dynamic process with profound implications for intellectual growth and application in diverse real-world contexts.

The Nature of Problem Solving

Problem solving, within the realm of psychology, refers to the cognitive process through which individuals identify, analyze, and resolve challenges or obstacles to achieve a desired goal. It encompasses a range of mental activities, such as perception, memory, reasoning, and decision-making, aimed at devising effective solutions in the face of uncertainty or complexity.

Problem solving as a subject of inquiry has drawn from various theoretical perspectives, each offering unique insights into its nature. Among the seminal theories, Gestalt psychology has highlighted the role of insight and restructuring in problem solving, emphasizing that individuals often reorganize their mental representations to attain solutions. Information processing theories, inspired by computer models, emphasize the systematic and step-by-step nature of problem solving, likening it to information retrieval and manipulation. Furthermore, cognitive psychology has provided a comprehensive framework for understanding problem solving by examining the underlying cognitive processes involved, such as attention, memory, and decision-making. These theoretical foundations collectively offer a richer comprehension of how humans engage in and approach problem-solving tasks.

Problem solving is not a monolithic process but a series of interrelated stages that individuals progress through. These stages are integral to the overall problem-solving process, and they include:

• Problem Representation: At the outset, individuals must clearly define and represent the problem they face. This involves grasping the nature of the problem, identifying its constraints, and understanding the relationships between various elements.
• Goal Setting: Setting a clear and attainable goal is essential for effective problem solving. This step involves specifying the desired outcome or solution and establishing criteria for success.
• Solution Generation: In this stage, individuals generate potential solutions to the problem. This often involves brainstorming, creative thinking, and the exploration of different strategies to overcome the obstacles presented by the problem.
• Solution Evaluation: After generating potential solutions, individuals must evaluate these alternatives to determine their feasibility and effectiveness. This involves comparing solutions, considering potential consequences, and making choices based on the criteria established in the goal-setting phase.

These components collectively form the roadmap for navigating the terrain of problem solving and provide a structured approach to addressing challenges effectively. Understanding these stages is crucial for both researchers studying problem solving and educators aiming to foster problem-solving skills in learners.

Cognitive and Psychological Aspects of Problem Solving

Problem solving is intricately tied to a range of cognitive processes, each contributing to the effectiveness of the problem-solving endeavor.

• Perception: Perception serves as the initial gateway in problem solving. It involves the gathering and interpretation of sensory information from the environment. Effective perception allows individuals to identify relevant cues and patterns within a problem, aiding in problem representation and understanding.
• Memory: Memory is crucial in problem solving as it enables the retrieval of relevant information from past experiences, learned strategies, and knowledge. Working memory, in particular, helps individuals maintain and manipulate information while navigating through the various stages of problem solving.
• Reasoning: Reasoning encompasses logical and critical thinking processes that guide the generation and evaluation of potential solutions. Deductive and inductive reasoning, as well as analogical reasoning, play vital roles in identifying relationships and formulating hypotheses.

While problem solving is a universal cognitive function, individuals differ in their problem-solving skills due to various factors.

• Intelligence: Intelligence, as measured by IQ or related assessments, significantly influences problem-solving abilities. Higher levels of intelligence are often associated with better problem-solving performance, as individuals with greater cognitive resources can process information more efficiently and effectively.
• Creativity: Creativity is a crucial factor in problem solving, especially in situations that require innovative solutions. Creative individuals tend to approach problems with fresh perspectives, making novel connections and generating unconventional solutions.
• Expertise: Expertise in a specific domain enhances problem-solving abilities within that domain. Experts possess a wealth of knowledge and experience, allowing them to recognize patterns and solutions more readily. However, expertise can sometimes lead to domain-specific biases or difficulties in adapting to new problem types.

Despite the cognitive processes and individual differences that contribute to effective problem solving, individuals often encounter barriers that impede their progress. Recognizing and overcoming these barriers is crucial for successful problem solving.

• Functional Fixedness: Functional fixedness is a cognitive bias that limits problem solving by causing individuals to perceive objects or concepts only in their traditional or “fixed” roles. Overcoming functional fixedness requires the ability to see alternative uses and functions for objects or ideas.
• Confirmation Bias: Confirmation bias is the tendency to seek, interpret, and remember information that confirms preexisting beliefs or hypotheses. This bias can hinder objective evaluation of potential solutions, as individuals may favor information that aligns with their initial perspectives.
• Mental Sets: Mental sets are cognitive frameworks or problem-solving strategies that individuals habitually use. While mental sets can be helpful in certain contexts, they can also limit creativity and flexibility when faced with new problems. Recognizing and breaking out of mental sets is essential for overcoming this barrier.

Understanding these cognitive processes, individual differences, and common obstacles provides valuable insights into the intricacies of problem solving and offers a foundation for improving problem-solving skills and strategies in both educational and practical settings.

Problem Solving in Educational Settings

Problem solving holds a central position in educational psychology, as it is a fundamental skill that empowers students to navigate the complexities of the learning process and prepares them for real-world challenges. It goes beyond rote memorization and standardized testing, allowing students to apply critical thinking, creativity, and analytical skills to authentic problems. Problem-solving tasks in educational settings range from solving mathematical equations to tackling complex issues in subjects like science, history, and literature. These tasks not only bolster subject-specific knowledge but also cultivate transferable skills that extend beyond the classroom.

Problem-solving skills offer numerous advantages to both educators and students. For teachers, integrating problem-solving tasks into the curriculum allows for more engaging and dynamic instruction, fostering a deeper understanding of the subject matter. Additionally, it provides educators with insights into students’ thought processes and areas where additional support may be needed. Students, on the other hand, benefit from the development of critical thinking, analytical reasoning, and creativity. These skills are transferable to various life situations, enhancing students’ abilities to solve complex real-world problems and adapt to a rapidly changing society.

Teaching problem-solving skills is a dynamic process that requires effective pedagogical approaches. In K-12 education, educators often use methods such as the problem-based learning (PBL) approach, where students work on open-ended, real-world problems, fostering self-directed learning and collaboration. Higher education institutions, on the other hand, employ strategies like case-based learning, simulations, and design thinking to promote problem solving within specialized disciplines. Additionally, educators use scaffolding techniques to provide support and guidance as students develop their problem-solving abilities. In both K-12 and higher education, a key component is metacognition, which helps students become aware of their thought processes and adapt their problem-solving strategies as needed.

Assessing problem-solving abilities in educational settings involves a combination of formative and summative assessments. Formative assessments, including classroom discussions, peer evaluations, and self-assessments, provide ongoing feedback and opportunities for improvement. Summative assessments may include standardized tests designed to evaluate problem-solving skills within a particular subject area. Performance-based assessments, such as essays, projects, and presentations, offer a holistic view of students’ problem-solving capabilities. Rubrics and scoring guides are often used to ensure consistency in assessment, allowing educators to measure not only the correctness of answers but also the quality of the problem-solving process. The evolving field of educational technology has also introduced computer-based simulations and adaptive learning platforms, enabling precise measurement and tailored feedback on students’ problem-solving performance.

Understanding the pivotal role of problem solving in educational psychology, the diverse pedagogical strategies for teaching it, and the methods for assessing and measuring problem-solving abilities equips educators and students with the tools necessary to thrive in educational environments and beyond. Problem solving remains a cornerstone of 21st-century education, preparing students to meet the complex challenges of a rapidly changing world.

Applications and Practical Implications

Problem solving is not confined to the classroom; it extends its influence to various real-world contexts, showcasing its relevance and impact. In business, problem solving is the driving force behind product development, process improvement, and conflict resolution. For instance, companies often use problem-solving methodologies like Six Sigma to identify and rectify issues in manufacturing. In healthcare, medical professionals employ problem-solving skills to diagnose complex illnesses and devise treatment plans. Additionally, technology advancements frequently stem from creative problem solving, as engineers and developers tackle challenges in software, hardware, and systems design. Real-world problem solving transcends specific domains, as individuals in diverse fields address multifaceted issues by drawing upon their cognitive abilities and creative problem-solving strategies.

Clinical psychology recognizes the profound therapeutic potential of problem-solving techniques. Problem-solving therapy (PST) is an evidence-based approach that focuses on helping individuals develop effective strategies for coping with emotional and interpersonal challenges. PST equips individuals with the skills to define problems, set realistic goals, generate solutions, and evaluate their effectiveness. This approach has shown efficacy in treating conditions like depression, anxiety, and stress, emphasizing the role of problem-solving abilities in enhancing emotional well-being. Furthermore, cognitive-behavioral therapy (CBT) incorporates problem-solving elements to help individuals challenge and modify dysfunctional thought patterns, reinforcing the importance of cognitive processes in addressing psychological distress.

Problem solving is the bedrock of innovation and creativity in various fields. Innovators and creative thinkers use problem-solving skills to identify unmet needs, devise novel solutions, and overcome obstacles. Design thinking, a problem-solving approach, is instrumental in product design, architecture, and user experience design, fostering innovative solutions grounded in human needs. Moreover, creative industries like art, literature, and music rely on problem-solving abilities to transcend conventional boundaries and produce groundbreaking works. By exploring alternative perspectives, making connections, and persistently seeking solutions, creative individuals harness problem-solving processes to ignite innovation and drive progress in all facets of human endeavor.

Understanding the practical applications of problem solving in business, healthcare, technology, and its therapeutic significance in clinical psychology, as well as its indispensable role in nurturing innovation and creativity, underscores its universal value. Problem solving is not only a cognitive skill but also a dynamic force that shapes and improves the world we inhabit, enhancing the quality of life and promoting progress and discovery.

In summary, problem solving stands as an indispensable cornerstone within the domains of psychology and education. This article has explored the multifaceted nature of problem solving, from its theoretical foundations rooted in Gestalt psychology, information processing theories, and cognitive psychology to its integral components of problem representation, goal setting, solution generation, and solution evaluation. It has delved into the cognitive processes underpinning effective problem solving, including perception, memory, and reasoning, as well as the impact of individual differences such as intelligence, creativity, and expertise. Common barriers to problem solving, including functional fixedness, confirmation bias, and mental sets, have been examined in-depth.

The significance of problem solving in educational settings was elucidated, underscoring its pivotal role in fostering critical thinking, creativity, and adaptability. Pedagogical approaches and assessment methods were discussed, providing educators with insights into effective strategies for teaching and evaluating problem-solving skills in K-12 and higher education.

Furthermore, the practical implications of problem solving were demonstrated in the real world, where it serves as the driving force behind advancements in business, healthcare, and technology. In clinical psychology, problem-solving therapies offer effective interventions for emotional and psychological well-being. The symbiotic relationship between problem solving and innovation and creativity was explored, highlighting the role of this cognitive process in pushing the boundaries of human accomplishment.

As we conclude, it is evident that problem solving is not merely a skill but a dynamic process with profound implications. It enables individuals to navigate the complexities of their environment, fostering intellectual growth, adaptability, and innovation. Future research in the field of problem solving should continue to explore the intricate cognitive processes involved, individual differences that influence problem-solving abilities, and innovative teaching methods in educational settings. In practice, educators and clinicians should continue to incorporate problem-solving strategies to empower individuals with the tools necessary for success in education, personal development, and the ever-evolving challenges of the real world. Problem solving remains a steadfast ally in the pursuit of knowledge, progress, and the enhancement of human potential.

References:

• Anderson, J. R. (1995). Cognitive psychology and its implications. W. H. Freeman.
• Atkinson, R. C., & Shiffrin, R. M. (1968). Human memory: A proposed system and its control processes. In The psychology of learning and motivation (Vol. 2, pp. 89-195). Academic Press.
• Duncker, K. (1945). On problem-solving. Psychological Monographs, 58(5), i-113.
• Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology, 12(3), 306-355.
• Jonassen, D. H., & Hung, W. (2008). All problems are not equal: Implications for problem-based learning. Interdisciplinary Journal of Problem-Based Learning, 2(2), 6.
• Kitchener, K. S., & King, P. M. (1981). Reflective judgment: Concepts of justification and their relation to age and education. Journal of Applied Developmental Psychology, 2(2), 89-116.
• Luchins, A. S. (1942). Mechanization in problem solving: The effect of Einstellung. Psychological Monographs, 54(6), i-95.
• Mayer, R. E. (1992). Thinking, problem solving, cognition. W. H. Freeman.
• Newell, A., & Simon, H. A. (1972). Human problem solving (Vol. 104). Prentice-Hall Englewood Cliffs, NJ.
• Osborn, A. F. (1953). Applied imagination: Principles and procedures of creative problem solving (3rd ed.). Charles Scribner’s Sons.
• Polya, G. (1945). How to solve it: A new aspect of mathematical method. Princeton University Press.
• Sternberg, R. J. (2003). Wisdom, intelligence, and creativity synthesized. Cambridge University Press.