cs224n assignment 5 solutions

Assignment 5

Handout: CS 224N: Assignment 5: Self-Attention, Transformers, and Pretraining

1. Attention Exploration

(a). copying in attention.

\(\alpha\) is calculating the softmax of \(k_i^T q\) which makes it like a categorical probability distribution.

To make \(\alpha_j \gg \sum_{i \neq j} \alpha_i\) for some \(j\) . \(k_j^T q \gg k_i^T q, \forall i\neq j\) is required.

under conditions give in ii. \(c\approx v_j\)

Intuitively, the larger \(\alpha_i\) is, the higher attention is given on \(v_i\) in the output \(c\) .

(b). An average of two

Let $$ M=\left[\begin{array}{c} a_{1}^{\top} \\ \vdots \\ a_{m}^{\top} \end{array}\right] $$ then, \(Ms = M(v_a+v_b)=v_a\)

(c). Drawbacks of single-headed attention

Since the variance is small, we can treat \(k_i\) as concentrating around \(\mu_i\) , so $$ q=\beta(\mu_a+\mu_b), \beta\gg 0 $$

As the figures shows, \(k_a\) might ahve larger or smaller magnitude comparing with \(\mu_a\) . To make an estimation, we can assume \(k_a\approx \gamma \mu_a, \gamma \sim N(1, \frac{1}{2})\) , so $$ c \approx \frac{\exp (\gamma \beta)}{\exp (\gamma \beta)+\exp (\beta)} v_{a}+\frac{\exp (\beta)}{\exp (\gamma \beta)+\exp (\beta)} v_{b} =\frac{1}{\exp ((1-\gamma) \beta)+1} v_{a}+\frac{1}{\exp ((\gamma-1) \beta)+1} v_{b} $$ i.e. \(c\) will oscillates between \(v_a\) and \(v_b\) as sampling \({k_1, k_2, ..., k_n}\) multiple times.

(d). Benefits of multi-headed attention

• \(q_1=q_2=\beta(\mu_a+\mu_b), \beta \gg 0\)
• \(q_1 = \mu_a, q_2 = \mu_b\) , or vice versa.

Under two circumstances in i. 1. Averaging between different samples makes \(k_a\) closer to its expectation \(\mu_a\) , the result is that \(c\) is closer to \(\frac{1}{2}(v_a+v_b)\) . 2. \(c\) is always approximately \(\frac{1}{2}(v_a+v_b)\) , exactly when \(\alpha=0\) .

2. Pretrained Transformer models and knowledge access

Implementation: Assignment 5 Code

(g). sythesize variant

The single sythesizer can't capture the inter-dimension relative importance.

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

This repository contains my solutions to the assignments for Stanford's CS224n "Natural Language Processing with Deep Learning" (Winter 2021).

amanchadha/stanford-cs224n-assignments-2021

Folders and files, repository files navigation, stanford course cs224n - natural language processing with deep learning (winter 2021).

These are my solutions to the assignments of CS224n (Natural Language Processing with Deep Learning) offered by Stanford University in Winter 2021. There are five assignments in total. Here is a brief description of each one of these assignments:

Assignment 1. Word Embeddings

• This assignment [ notebook , PDF ] has two parts which deal with representing words with dense vectors (i.e., word vectors or word embeddings). Word vectors are often used as a fundamental component for downstream NLP tasks, e.g. question answering, text generation, translation, etc., so it is important to build some intuitions as to their strengths and weaknesses. Here, you will explore two types of word vectors: those derived from co-occurrence matrices (which uses SVD), and those derived via GloVe (based on maximum-likelihood training in ML).

1. Count-Based Word Vectors

• Many word vector implementations are driven by the idea that similar words, i.e., (near) synonyms, will be used in similar contexts. As a result, similar words will often be spoken or written along with a shared subset of words, i.e., contexts. By examining these contexts, we can try to develop embeddings for our words. With this intuition in mind, many "old school" approaches to constructing word vectors relied on word counts. Here we elaborate upon one of those strategies, co-occurrence matrices.
• In this part, you will use co-occurence matrices to develop dense vectors for words. A co-occurrence matrix counts how often different terms co-occur in different documents. To derive a co-occurence matrix, we use a window with a fixed size w , and then slide this window over all of the documents. Then, we count how many times two different words v i and v j occurs with each other in a window, and put this number in the (i, j) th entry of the matrix. We then run dimensionality reduction on the co-occurence matrix using singular value decomposition. We then select the top r components after the decomposition and thus, derive r -dimensional embeddings for words.

2. Prediction (or Maximum Likelihood)-Based Word Vectors: Word2Vec

• Prediction-based word vectors (which also utilize the benefit of counts) such as Word2Vec and GloVe have demonstrated better performance compared to co-occurence matrices. In this part, you will explore pretrained GloVe embeddings using the Gensim package. Initially, you'll have to reduce the dimensionality of word vectors using SVD from 300 to 2 to be able to vizualize and analyze these vectors. Next, you'll find the closest word vectors to a given word vector. You'll then get to know words with multiple meanings (polysemous words). You will also experiment with the analogy task, introduced for the first time in the Word2Vec paper (Mikolov et al. 2013) . The task is simple: given words x, y , and z , you have to find a word w such that the following relationship holds: x is to y like z is to w . For example, Rome is to Italy like D.C. is to the United States. You will find that solving this task with Word2Vec vectors is easy and is just a simple addition and subtraction of vectors, which is a nice feature of word embeddings.
• If you’re feeling adventurous, challenge yourself and try reading GloVe’s original paper .

Assignment 2. Understanding and Implementing Word2Vec

• In this assignment , you will get familiar with the Word2Vec algorithm. The key insight behind Word2Vec is that "a word is known by the company it keeps". There are two models introduced by the Word2Vec paper based on this idea: (i) the skip-gram model and (ii) the Continuous Bag Of Words (CBOW) model.
• In this assignment, you'll be implementing the skip-gram model using NumPy. You have to implement the both version of Skip-gram; the first one is with the naive Softmax loss and the second one -- which is much faster -- with the negative sampling loss. Your implementation of the first version is just sanity-checked on a small dataset, but you have to run the second version on the Stanford Sentiment Treebank dataset.
• It is highly recommend for anyone interested in gaining a deep understanding of Word2Vec to first do the theoretical part of this assignment and only then proceed to the practical part.

Assignment 3. Neural Dependency Parsing

• If you have take a compiler course before, you have definitely heard the term "parsing". This assignment is about "dependency parsing" where you train a model that can specify the dependencies. If you remember "Shift-Reduce Parser" from your Compiler class, then you will find the ideas here quite familiar. The only difference is that we shall use a neural network to find the dependencies. In this assignment, you will build a neural dependency parser using PyTorch.
• In Part 1 of this assignment , you will learn about two general neural network techniques (Adam Optimization and Dropout). In Part 2 of this assignment, you will implement and train a dependency parser using the techniques from Part 1, before analyzing a few erroneous dependency parses.
• Both the Adam optimizer and Dropout will be used in the neural dependency parser you are going to implement with PyTorch. The parser will do one of the following three moves: 1) Shift 2) Left-arc 3) Right-arc. You can read more about the details of these three moves in the handout of the assignment. What your network should do is to predict one of these moves at every step. For predicting each move, your model needs features which are going to be extracted from the stack and buffer of each stage (you maintain a stack and buffer during parsing, to know what you have already parsed and what is remaining for parsing, respectively). The good news is that the code for extracting features is given to you to help you just focus on the neural network part! There are lots of hints throughout the assignment -- as this is the first assignment in the course where students work with PyTorch -- that walk you through implementing each part.

Assignment 4. Seq2Seq Machine Translation Model with Multiplicative Attention

• This assignment is split into two sections: Neural Machine Translation with RNNs and Analyzing NMT Systems. The first is primarily coding and implementation focused, whereas the second entirely consists of written, analysis questions.

Assignment 5. Self-Attention, Transformers, and Pretraining

• Mathematical exploration: What kinds of operations can self-attention easily implement? Why should we use fancier things like multi-headed self-attention? This section will use some mathematical investigations to illuminate a few of the motivations of self-attention and Transformer networks.
• Extending a research codebase: In this portion of the assignment, you’ll get some experience and intuition for a cutting-edge research topic in NLP: teaching NLP models facts about the world through pretraining, and accessing that knowledge through finetuning. You’ll train a Transformer model to attempt to answer simple questions of the form “Where was person [x] born?” – without providing any input text from which to draw the answer. You’ll find that models are able to learn some facts about where people were born through pretraining, and access that information during fine-tuning to answer the questions.
• Then, you’ll take a harder look at the system you built, and reason about the implications and concerns about relying on such implicit pretrained knowledge.

• Assignment 1: Intro to word vectors a1/exploring_word_vectors.ipynb
• Assignment 2: Training Word2Vec a2/a2.pdf
• Assignment 3: Dependency parsing a3/a3.pdf
• Assignment 4: Neural machine translation with seq2seq and attention a4/a4.pdf
• Assignment 5: Neural machine translation with sub-word modeling a5/a5.pdf
• Project: SQuAD - Stanford Question Asking Dataset project/proposal.pdf

Prerequisites

• Proficiency in Python. All class assignments will be in Python (using NumPy and PyTorch). If you need to remind yourself of Python, or you're not very familiar with NumPy, attend the Python review session in week 1 (listed in the schedule). If you have a lot of programming experience but in a different language (e.g. C/C++/Matlab/Java/Javascript), you will probably be fine.
• College Calculus, Linear Algebra (e.g. MATH51, CME100). You should be comfortable taking (multivariable) derivatives and understanding matrix/vector notation and operations.
• Basic Probability and Statistics (e.g. CS109 or equivalent) You should know basics of probabilities, Gaussian distributions, mean, standard deviation, etc.
• Foundations of Machine Learning (e.g. CS221 or CS229). We will be formulating cost functions, taking derivatives and performing optimization with gradient descent. If you already have basic machine learning and/or deep learning knowledge, the course will be easier; however it is possible to take CS224n without it. There are many introductions to ML, in webpage, book, and video form. One approachable introduction is Hal Daumé's in-progress "A Course in Machine Learning". Reading the first 5 chapters of that book would be good background. Knowing the first 7 chapters would be even better!

Course Description

• This course was formed in 2017 as a merger of the earlier CS224n (Natural Language Processing) and CS224d (Natural Language Processing with Deep Learning) courses. Below you can find archived websites and student project reports.
• Natural language processing (NLP) is one of the most important technologies of the information age, and a crucial part of artificial intelligence. Applications of NLP are everywhere because people communicate almost everything in language: web search, advertising, emails, customer service, language translation, medical reports, etc. In recent years, Deep Learning approaches have obtained very high performance across many different NLP tasks, using single end-to-end neural models that do not require traditional, task-specific feature engineering. In this course, students will gain a thorough introduction to cutting-edge research in Deep Learning for NLP. Through lectures, assignments and a final project, students will learn the necessary skills to design, implement, and understand their own neural network models. CS224n uses PyTorch.

Lecture notes, assignments and other materials can be downloaded from the course webpage .

• Lectures: YouTube
• Schedule: Stanford CS224n
• Projects: Stanford CS224n

I recognize the hard time people spend on building intuition, understanding new concepts and debugging assignments. The solutions uploaded here are only for reference . They are meant to unblock you if you get stuck somewhere. Please do not copy any part of the solutions as-is (the assignments are fairly easy if you read the instructions carefully).

Contributors 2

• Jupyter Notebook 57.5%
• Python 40.6%
• JavaScript 1.2%

• 0.00  $ 0 items

CS224N: Assignment 5: Self-Attention, Transformers, and Pretraining Q1 a, b, c, d Solved

35.00  $

You'll get a download link with a: pdf solution files instantly, after Payment

If Helpful Share:

Description

This assignment is an investigation into Transformer self-attention building blocks, and the effects of pretraining. It covers mathematical properties of Transformers and self-attention through written questions. Further, you’ll get experience with practical system-building through repurposing an existing codebase. The assignment is split into a written (mathematical) part and a coding part, with its own written questions. Here’s a quick summary:

• Mathematical exploration: What kinds of operations can self-attention easily implement? Why should we use fancier things like multi-headed self-attention? This section will use some mathematical investigations to illuminate a few of the motivations of self-attention and Transformer networks. Note: for all questions, you should justify your answer with mathematical reasoning when required.
• Extending a research codebase: In this portion of the assignment, you’ll get some experience and intuition for a cutting-edge research topic in NLP: teaching NLP models facts about the world through pretraining, and accessing that knowledge through finetuning. You’ll train a Transformer model to attempt to answer simple questions of the form “Where was person [x] born?” – without providing any input text from which to draw the answer. You’ll find that models are able to learn some facts about where people were born through pretraining, and access that information during fine-tuning to answer the questions.

Then, you’ll take a harder look at the system you built, and reason about the implications and concerns about relying on such implicit pretrained knowledge.

This assignment was originally created by John Hewitt, CS 224N Head TA in Winter 2021.

1.     Attention exploration (22 points)

Multi-headed self-attention is the core modeling component of Transformers. In this question, we’ll get some practice working with the self-attention equations, and motivate why multi-headed self-attention can be preferable to single-headed self-attention.

Recall that attention can be viewed as an operation on a query q ∈ R d , a set of value vectors { v 1 ,…,v n } ,v i ∈ R d , and a set of key vectors { k 1 ,…,k n } ,k i ∈ R d , specified as follows:

c = ∑ v i α i                                                                                                                                        (1)

with α i termed the “attention weights”. Observe that the output c ∈ R d is an average over the value vectors weighted with respect to α i .

• (1 point) Explain why α can be interpreted as a categorical probability distribution.
• (2 points) The distribution α is typically relatively “diffuse”; the probability mass is spread out between many different α i . However, this is not always the case. Describe (in one sentence) under what conditions the categorical distribution α puts almost all of its weight on some α j , where j ∈ {1 ,…,n } (i.e. α j ≫ ∑ i ̸ = j α i ). What must be true about the query q and/or the keys { k 1 ,…,k n }?
• (1 point) Under the conditions you gave in (ii), describe what properties the output c might have. iv. (1 point) Explain (in two sentences or fewer) what your answer to (ii) and (iii) means intuitively.
• (3 points) How should we combine two d -dimensional vectors v a ,v b into one output vector c in a way that preserves information from both vectors? In machine learning, one common way to do so is to take the average: . It might seem hard to extract information about the original vectors v a and v b from the resulting c , but under certain conditions one can do so. In this problem, we’ll see why this is the case.

Suppose that although we don’t know v a or v b , we do know that v a lies in a subspace A formed by the m basis vectors { a 1 ,a 2 ,…,a m }, while v b lies in a subspace B formed by the p basis vectors { b 1 ,b 2 ,…,b p } . (This means that any v a can be expressed as a linear combination of its basis vectors, as can v b . All basis vectors have norm 1 and orthogonal to each other.) Additionally, suppose that the two subspaces are orthogonal; i.e. a ⊤ j b k = 0 for all j,k .

Using the basis vectors { a 1 ,a 2 ,…,a m }, construct a matrix M such that for arbitrary vectors v a ∈ A and v b ∈ B , we can use M to extract v a from the sum vector s = v a + v b . In other words, we want to construct M such that for any v a ,v b , Ms = v a ).

Note: both M and v a ,v b should be expressed as a vector in R d , not in terms of vectors from A and B .

Hint: Given that the vectors { a 1 ,a 2 ,…,a m } are both orthogonal and form a basis for v a , we know that there exist some c 1 ,c 2 ,…,c m such that v a = c 1 a 1 + c 2 a 2 + ··· + c m a m . Can you create a vector of these weights c ? ii. (4 points) As before, let v a and v b be two value vectors corresponding to key vectors k a and k b , respectively. Assume that (1) all key vectors are orthogonal, so k i ⊤ k j for all i ≠ j ; and (2) all key vectors have norm 1. [1] Find an expression for a query vector q such that.

• (2 points) Assume that the covariance matrices are Σ i = αI ∀ i ∈ {1 , [2] ,…,n }, for vanishingly small α . Design a query q in terms of the µ i such that as before,, and provide a brief argument as to why it works.
• (3 points) Though single-headed attention is resistant to small perturbations in the keys, some types of larger perturbations may pose a bigger issue. Specifically, in some cases, one key vector k a may be larger or smaller in norm than the others, while still pointing in the same direction as µ a . As an example, let us consider a covariance for item for vanishingly small α (as shown in figure 1). This causes k a to point in roughly the same direction as µ a , but with large variances in magnitude. Further, let Σ i = αI for all i ≠ a .

Figure 1: The vector µ a (shown here in 2D as an example), with the range of possible values of k a shown in red. As mentioned previously, k a points in roughly the same direction as µ a , but may have larger or smaller magnitude.

When you sample { k 1 ,…,k n } multiple times, and use the q vector that you defined in part i., what qualitatively do you expect the vector c will look like for different samples?

• (3 points) Benefits of multi-headed attention: Now we’ll see some of the power of multi-headed attention. We’ll consider a simple version of multi-headed attention which is identical to singleheaded self-attention as we’ve presented it in this homework, except two query vectors ( q 1 and q 2 ) are defined, which leads to a pair of vectors ( c 1 and c 2 ), each the output of single-headed attention given its respective query vector. The final output of the multi-headed attention is their average,

. As in question 1(c), consider a set of key vectors { k 1 ,…,k n } that are randomly sampled, k i ∼ N( µ i , Σ i ), where the means µ i are known to you, but the covariances Σ i are unknown. Also as before, assume that the means µ i are mutually orthogonal; µ ⊤ i µ j = 0 if i ≠ j , and unit norm, ∥ µ i ∥ = 1.

• (1 point) Assume that the covariance matrices are Σ i = αI , for vanishingly small α . Design q 1 and q 2 such that c is approximately equal to .
• (2 points) Assume that the covariance matrices are for vanishingly small α , and Σ i = αI for all i ≠ a . Take the query vectors q 1 and q 2 that you designed in part i. What, qualitatively, do you expect the output c to look like across different samples of the key vectors? Please briefly explain why. You can ignore cases in which k a ⊤ q i < 0.

2.     Pretrained Transformer models and knowledge access (35 points)

You’ll train a Transformer to perform a task that involves accessing knowledge about the world – knowledge which isn’t provided via the task’s training data (at least if you want to generalize outside the training set). You’ll find that it more or less fails entirely at the task. You’ll then learn how to pretrain that Transformer on Wikipedia text that contains world knowledge, and find that finetuning that Transformer on the same knowledge-intensive task enables the model to access some of the knowledge learned at pretraining time. You’ll find that this enables models to perform considerably above chance on a held out development set.

The code you’re provided with is a fork of Andrej Karpathy’s minGPT . It’s nicer than most research code in that it’s relatively simple and transparent. The “GPT” in minGPT refers to the Transformer language model of OpenAI, originally described in this paper [1].

As in previous assignments, you will want to develop on your machine locally, then run training on Azure. You can use the same conda environment from previous assignments for local development, and the same process for training on Azure (see the CS224n Azure Guide for a refresher). Specifically, you’ll still be running “conda activate py37_pytorch” on the Azure machine. You’ll need around 5 hours for training, so budget your time accordingly!

Your work with this codebase is as follows:

• (0 points) Check out the demo.

In the mingpt-demo/ folder is a Jupyter notebook that trains and samples from a Transformer language model. Take a look at it (locally on your computer) to get somewhat familiar with how it defines and trains models. Some of the code you’re writing below will be inspired by what you see in this notebook.

Note that you do not have to write any code or submit written answers for this part.

• (0 points) Read through NameDataset , our dataset for reading name-birthplace pairs.

The task we’ll be working on with our pretrained models is attempting to access the birth place of a notable person, as written in their Wikipedia page. We’ll think of this as a particularly simple form of question answering:

Q: Where was [person] born?

From now on, you’ll be working with the src/ folder. The code in mingpt-demo/ won’t be changed or evaluated for this assignment. In dataset.py, you’ll find the the class NameDataset, which reads a TSV (tab-separated values) file of name/place pairs and produces examples of the above form that we can feed to our Transformer model.

To get a sense of the examples we’ll be working with, if you run the following code, it’ll load your NameDataset on the training set birth_places_train.tsv and print out a few examples.

python src/dataset.py namedata

(c) (0 points) Implement finetuning (without pretraining).

Take a look at run.py. It has some skeleton code specifying flags you’ll eventually need to handle as command line arguments. In particular, you might want to pretrain , finetune , or evaluate a model with this code. For now, we’ll focus on the finetuning function, in the case without pretraining.

Taking inspiration from the training code in the play_char.ipynb file, write code to finetune a Transformer model on the name/birthplace dataset, via examples from the NameDataset class. For now, implement the case without pretraining (i.e. create a model from scratch and train it on the birthplace prediction task from part (b)). You’ll have to modify two sections, marked [part c] in the code: one to initialize the model, and one to finetune it. Note that you only need to initialize the model in the case labeled “vanilla” for now (later in section (g), we will explore a model variant). Use the hyperparameters for the Trainer specified in the run.py code.

Also take a look at the evaluation code which has been implemented for you. It samples predictions from the trained model and calls evaluate_places() to get the total percentage of correct place predictions. You will run this code in part (d) to evaluate your trained models.

This is an intermediate step for later portions, including Part d, which contains commands you can run to check your implementation. No written answer is required for this part.

• (5 points) Make predictions (without pretraining).

Train your model on wiki.txt, and evaluate on birth_dev.tsv. Specifically, you should now be able to run the following three commands:

Training will take less than 10 minutes (on Azure). Report your model’s accuracy on the dev set (as printed by the second command above). Don’t be surprised if it is well below 10%; we will be digging into why in Part 3. As a reference point, we want to also calculate the accuracy the model would have achieved if it had just predicted “London” as the birth place for everyone in the dev set. Fill in london_baseline.py to calculate the accuracy of that approach and report your result in your write-up. You should be able to leverage existing code such that the file is only a few lines long.

• (10 points) Define a span corruption function for pretraining.

In the file src/dataset.py, implement the __getitem__() function for the dataset class CharCorruptionDataset. Follow the instructions provided in the comments in dataset.py. Span corruption is explored in the T5 paper [2]. It randomly selects spans of text in a document and replaces them with unique tokens (noising). Models take this noised text, and are required to output a pattern of each unique sentinel followed by the tokens that were replaced by that sentinel in the input. In this question, you’ll implement a simplification that only masks out a single sequence of characters.

This question will be graded via autograder based on whether your span corruption function implements some basic properties of our spec. We’ll instantiate the CharCorruptionDataset with our own data, and draw examples from it.

To help you debug, if you run the following code, it’ll sample a few examples from your CharCorruptionDataset on the pretraining dataset wiki.txt and print them out for you.

python src/dataset.py charcorruption

No written answer is required for this part.

• (10 points) Pretrain, finetune, and make predictions. Budget 2 hours for training.

Now fill in the pretrain portion of run.py, which will pretrain a model on the span corruption task. Additionally, modify your finetune portion to handle finetuning in the case with pretraining. In particular, if a path to a pretrained model is provided in the bash command, load this model before finetuning it on the birthplace prediction task. Pretrain your model on wiki.txt (which should take approximately two hours), finetune it on NameDataset and evaluate it. Specifically, you should be able to run the following four commands: (Don’t be concerned if the loss appears to plateau in the middle of pretraining; it will eventually go back down.)

Report the accuracy on the dev set (printed by the third command above). We expect the dev accuracy will be at least 10%, and will expect a similar accuracy on the held out test set.

• (10 points) Research! Write and try out the synthesizer variant (Budget 2 hours for pretraining!)

We’ll now go to changing the Transformer architecture itself – specifically, the self-attention module. While we’ve been using a self-attention scoring function based on dot products, this involves a rather intensive computation that’s quadratic in the sequence length. This is because the dot product between ℓ 2 pairs of word vectors is computed in each computation. Synthesized attention [3] is a very recent alternative that has potential benefits by removing this dot product (and quadratic computation) entirely. It’s a promising idea, and one way for us to ask, “What’s important/right about the Transformer architecture, and where can we improve/prune aspects of it?” In attention.py, implement the forward() method of SynthesizerAttention, which implements a variant of the Synthesizer proposed in the cited paper.

The provided CausalSelfAttention implements the following attention for each head of the multiheaded attention: Let X ∈ R ℓ × d (where ℓ is the block size and d is the total dimensionality, d/h is the dimensionality per head.). [3] Let Q,K,V ∈ R d × d/h . Then the output of the self-attention head is

Y i = softmax                              (3)

where Y i ∈ R ℓ × d/h . Then the output of the self-attention is a linear transformation of the concatenation of the heads:

Y = [ Y 1 ; … ; Y h ] A                                                   (4)

where A ∈ R d × d and [ Y 1 ; … ; Y h ] ∈ R ℓ × d . The code also includes dropout layers which we haven’t written here. We suggest looking at the provided code and noting how this equation is implemented in PyTorch.

Your job is to implement the following variant of attention. Instead of Equation 3, implement the following in SynthesizerAttention:

Y i = softmax(ReLU( XA i + b 1 ) B i + b 2 )( XV i ) ,                            (5)

where A i ∈ R d × d/h , B i ∈ R d/h × ℓ , and V i ∈ R d × d/h . [4] One way to interpret this is as follows: The term ( XQ i )( XK i )⊤ is an ℓ × ℓ matrix of attention scores, computed as all pairs of dot products between word embeddings. The synthesizer variant eschews the all-pairs dot product and directly computes the ℓ × ℓ matrix of attention scores by mapping each d -dimensional vector of each head for X to an ℓ -dimesional vector of unnormalized attention weights.

In the rest of the code in the src/ folder, modify your model to support using either CausalSelfAttention or SynthesizerAttention. Add the ability to switch between these attention variants depending on whether “vanilla” (for causal self-attention) or “synthesizer” (for the synthesizer variant) is selected in the command line arguments (see the section marked [part g] in src/run.py). You are free to implement this functionality in any way you choose, so long as it supports these command line arguments.

Below are bash commands that your code should support in order to pretrain the model, finetune it, and make predictions on the dev and test sets. Note that the pretraining process will take approximately 2 hours.

Report the accuracy of your synthesizer attention model on birthplace prediction on birth_dev.tsv after pretraining and fine-tuning.

• (8 points) We’ll score your model as to whether it gets at least 5% accuracy on the test set, which has answers held out.
• (2 points) Why might the synthesizer self-attention not be able to do, in a single layer, what the key-query-value self-attention can do?

3.     Considerations in pretrained knowledge (5 points)

Please type the answers to these written questions (to make TA lives easier).

• (1 point) Succinctly explain why the pretrained (vanilla) model was able to achieve an accuracy of above 10%, whereas the non-pretrained model was not.
• (2 points) Take a look at some of the correct predictions of the pretrain+finetuned vanilla model, as well as some of the errors. We think you’ll find that it’s impossible to tell, just looking at the output, whether the model retrieved the correct birth place, or made up an incorrect birth place. Consider the implications of this for user-facing systems that involve pretrained NLP components. Come up with two distinct reasons why this model behavior (i.e. unable to tell whether it’s retrieved or made up) may cause concern for such applications, and an example for each reason.
• (2 points) If your model didn’t see a person’s name at pretraining time, and that person was not seen at fine-tuning time either, it is not possible for it to have “learned” where they lived. Yet, your model will produce something as a predicted birth place for that person’s name if asked. Concisely describe a strategy your model might take for predicting a birth place for that person’s name, and one reason why this should cause concern for the use of such applications. (You do not need to submit the same answer for 3c as for 3b.)

Submission Instructions

You will submit this assignment on GradeScope as two submissions – one for Assignment 5 [coding] and another for Assignment 5 [written] :

• The no-pretraining model and predictions: vanilla.model.params, vanilla.nopretrain.dev.predictions, vanilla.nopretrain.test.predictions
• The pretrain-finetune model and predictions: vanilla.finetune.params, vanilla.pretrain.dev.predictions, vanilla.pretrain.test.predictions
• The synthesizer model and predictions: synthesizer.finetune.params, synthesizer.pretrain.dev.predictions, synthesizer.pretrain.test.predictions
• Run the collect_submission.sh script to produce your assignment5.zip file.
• Upload your assignment5.zip file to GradeScope to Assignment 5 [coding] .
• Check that the public autograder tests passed correctly.
• Upload your written solutions, for questions 1, parts of 2, and 3, to GradeScope to Assignment 5 [written] . Tag it properly!
• Radford, A., Narasimhan, K., Salimans, T., and Sutskever, I. Improving language understanding with unsupervised learning. Technical report, OpenAI (2018).
• Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., Zhou, Y., Li, W., and Liu, P. J. Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of Machine Learning Research 21 , 140 (2020), 1–67.
• Tay, Y., Bahri, D., Metzler, D., Juan, D.-C., Zhao, Z., and Zheng, C. Synthesizer: Rethinking self-attention in transformer models. arXiv preprint arXiv:2005.00743 (2020).

[1] Recall that a vector x has norm 1 iff x ⊤ x =1.

[2] Hint: while the softmax function will never exactly average the two vectors, you can get close by using a large scalar multiple in the expression.

[3] Note that these dimensionalities do not include the minibatch dimension.

[4] Hint: copy over the CausalSelfAttention class, and modify it minimally for this.

• a5_written_part-ceeb87.pdf

Related products

CS224N Assignment #3 Solved

Cs224n assignment #4 solved, cs 224n assignment #3: dependency parsing solved.

[email protected]

Whatsapp +1 -419-877-7882

• REFUND POLICY
• PRODUCT CATEGORIES
• GET HOMEWORK HELP
• C++ Programming Assignment
• Java Assignment Help
• MATLAB Assignment Help
• MySQL Assignment Help

• CS224N Stanford Lecture
• W1 What is the basic concept and Framework in NLP?
• W2 How to Calculate in Neural Network and What is the Dependency Parsing?
• W3 How to struct the Dependency Parsing and the Problem solved by RNN, Bi-RNN, GRU, LTSM?
• W4 Machine Translation, Sequence-to-Sequence, And Attention
• W5 Self-Attention and Transformers

CS224N W5. Self attention and Transformer

• Sep 27, 2021

All contents is arranged from CS224N contents. Please see the details to the CS224N !

1. Issue with recurrent models

$\checkmark$ Linear interaction distance

RNNs take O(sequence length) steps for distant word pairs to interact.

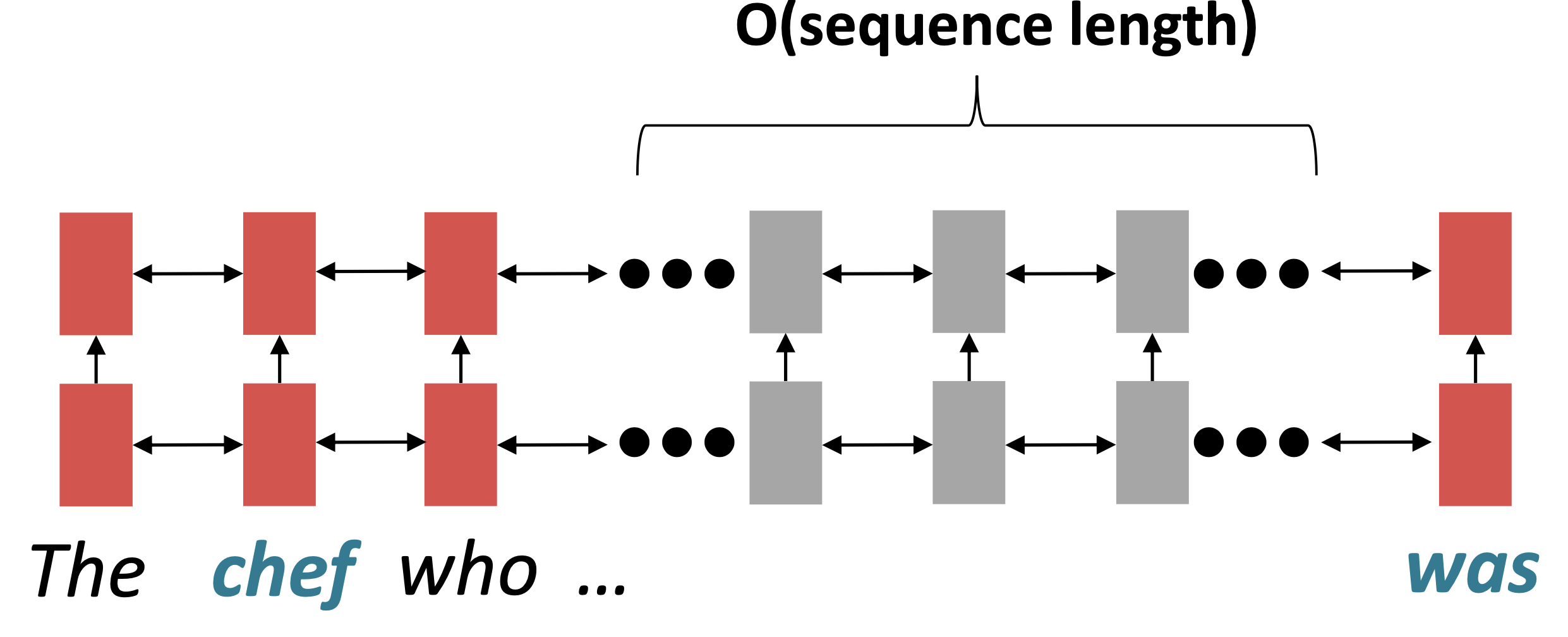
Reference. Stanford CS224n, 2021, Before word 'was', Information of chef has gone through O(sequence length) many layers!

It’s Hard to learn long-distance dependencies because of gradient problems. And linear order of words is “baked in”; we already know linear order isn’t the right way to think about sentences.

$\checkmark$ Lack of parallelizability

2. If not recurrence, then what?

2.1 word windows, also known as 1d convolution.

Word window models aggregate local contexts

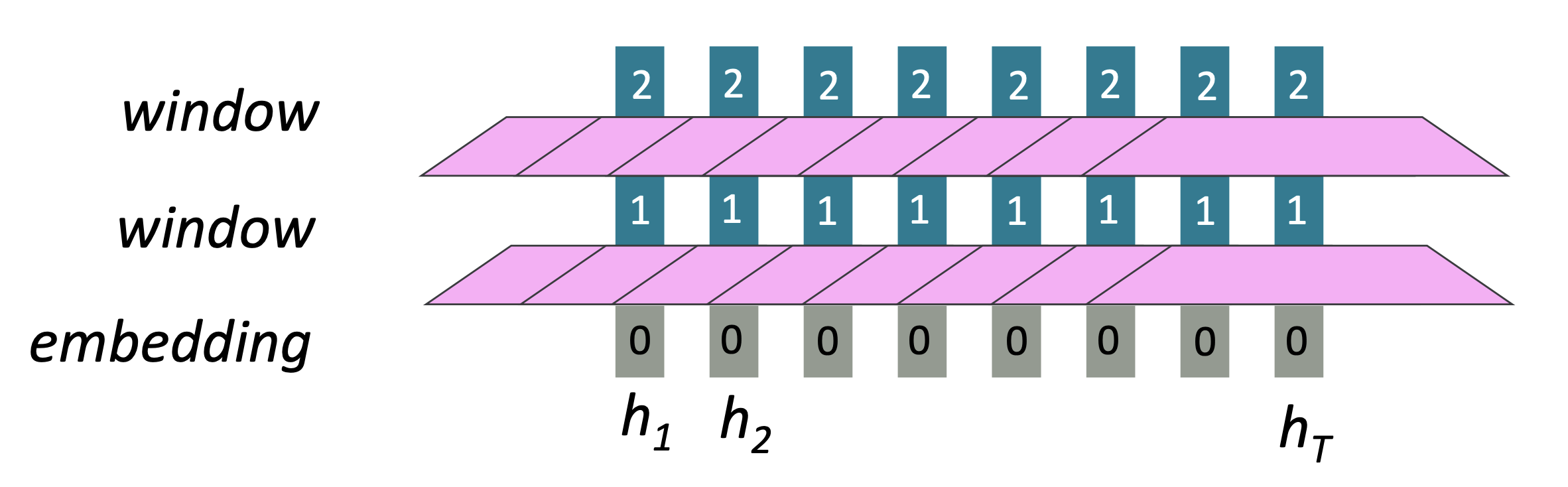
Reference. Stanford CS224n, 2021, Number of unparallelizable operations does not increase sequence length

• Long-distance dependencies: Stacking word window layers allows interaction between farther words
• Maximum Interaction distance  = sequence length / window size, but if sequence are too long, you’ll just ignore long-distance context

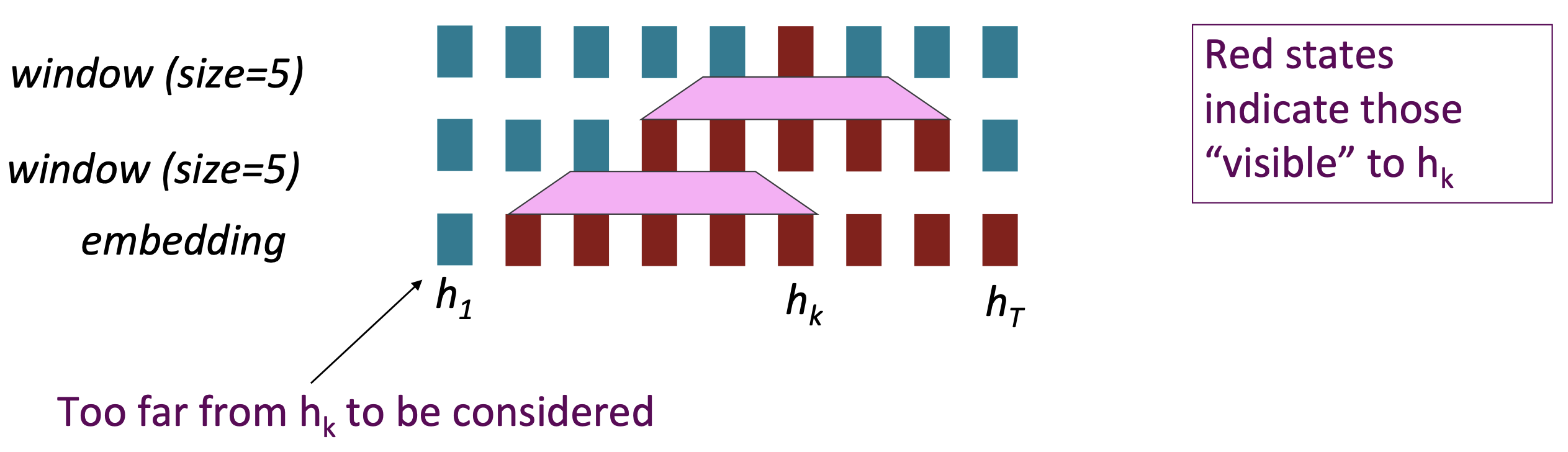
Reference. Stanford CS224n, 2021

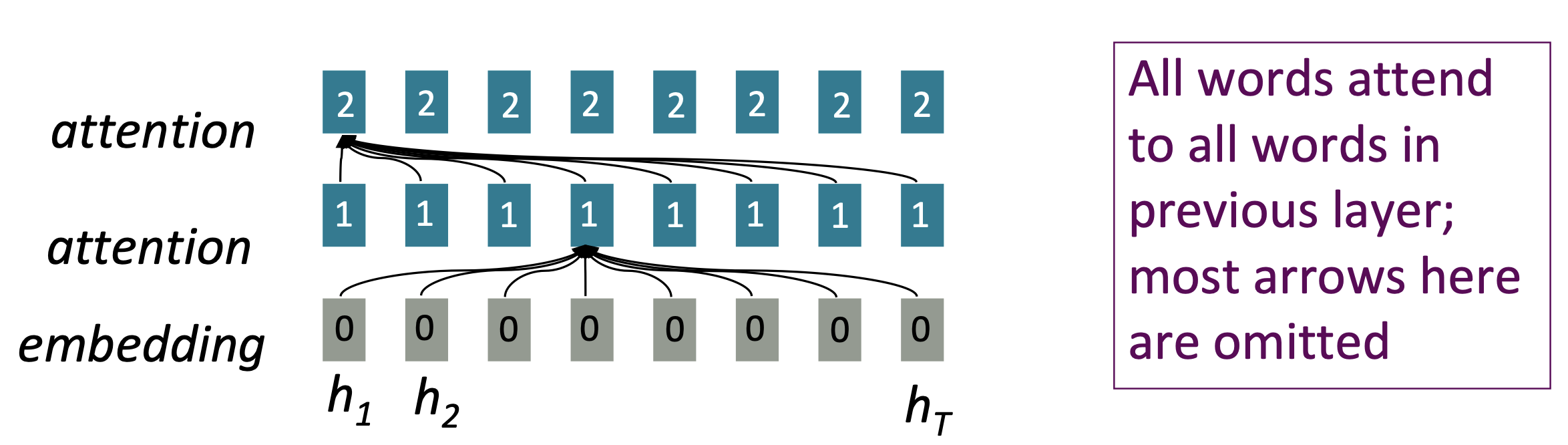
2.2 Attention

• Attention treats each word’s representation as a query to access and incorporate information from a set of values.
• Number of unparallelizable operations does not increase sequence length.
• Maximum interaction distance: O(1), since all words interact at every layer.

3. Self-Attention

• Reference. https://jalammar.github.io/illustrated-transformer/

3.1 Overview

Attention operates on  queries ,  keys , and  values.

In  self-attention , the queries, keys, and values are drawn from the same source.

For example, if the output of the previous layer is $𝑥_1, … , 𝑥_𝑇$, (one vec per word) we could let $𝑣_𝑖 = 𝑘_𝑖 = 𝑞_𝑖 = 𝑥_𝑖$ (that is, use the same vectors for all of them!).

In transformer model, it defines,

And we use V and K in encoder for decoder

Reference. Stanford CS224n, 2021, Self-attention is an operation on sets. It has no inherent notion of order.

Self-attention is an operation on  sets . It has no inherent notion of order.

3.2 Barriers and solutions for Self-Attention as a building block

$\checkmark$ 1. Doesn’t have an inherent notion for order → Add position representations to the inputs

Since self-attention doesn’t build in order information, we need to encode the order of the sentence in our keys, queries, and values. Consider representing each  sequence index  as a  vector

Easy to incorporate this info into our self-attention block: just add the 𝑝𝑖 to our inputs. Let $\tilde{v_i},\ \tilde{k_i},\ \tilde{q_i}$ be our old values, keys, and queries.

In deep self-attention networks, we do this at the first layer! You could concatenate them as well, but people mostly just add…

Method 1 Sinusoidal position representations.  

concatenate sinusoidal functions of varying periods:

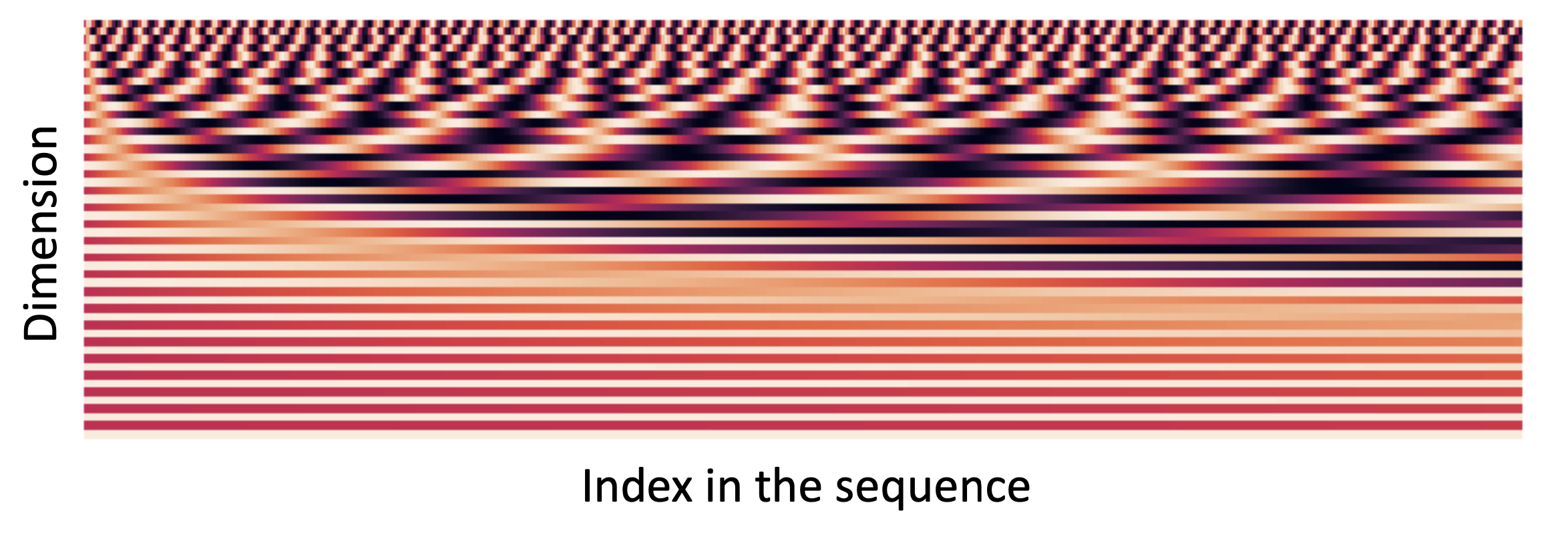
• Periodicity indicates that maybe “absolute position” isn’t as important
• Maybe can extrapolate to longer sequences as periods restart!
• Not learnable
• The extrapolation doesn’t really work!

Method 2 Position representation vectors learned from scratch.

• Learned absolute position representations: Let all $p_i$ be learnable parameters! Learn a matrix $𝑝 \in \mathbb{R}^{𝑑\times 𝑇}$ , and let each $p_i$   be a column of that matrix
• Pros: Flexibility, each position gets to be learned to fit the data
• Cons: Definitely can’t extrapolate to indices outside 1, … , 𝑇.

Most systems use this. Sometimes people try more flexible representations of position:

• Relative linear position attention  [Shaw et al., 2018]
• Dependency syntax-based position  [Wang et al., 2019]

$\checkmark$ 2. No nonlinearities for deep learning. It’s all just weighted averages → adding the same feedforward network to each self-attention output

Adding Nonlinearities in self-attention

Note that there are no elementwise nonlinearities in self-attention; stacking more self-attention layers just re-averages  value  vectors.

Add a feed-forward network to post-process each output vector($W_2, b_2$ in below equation)

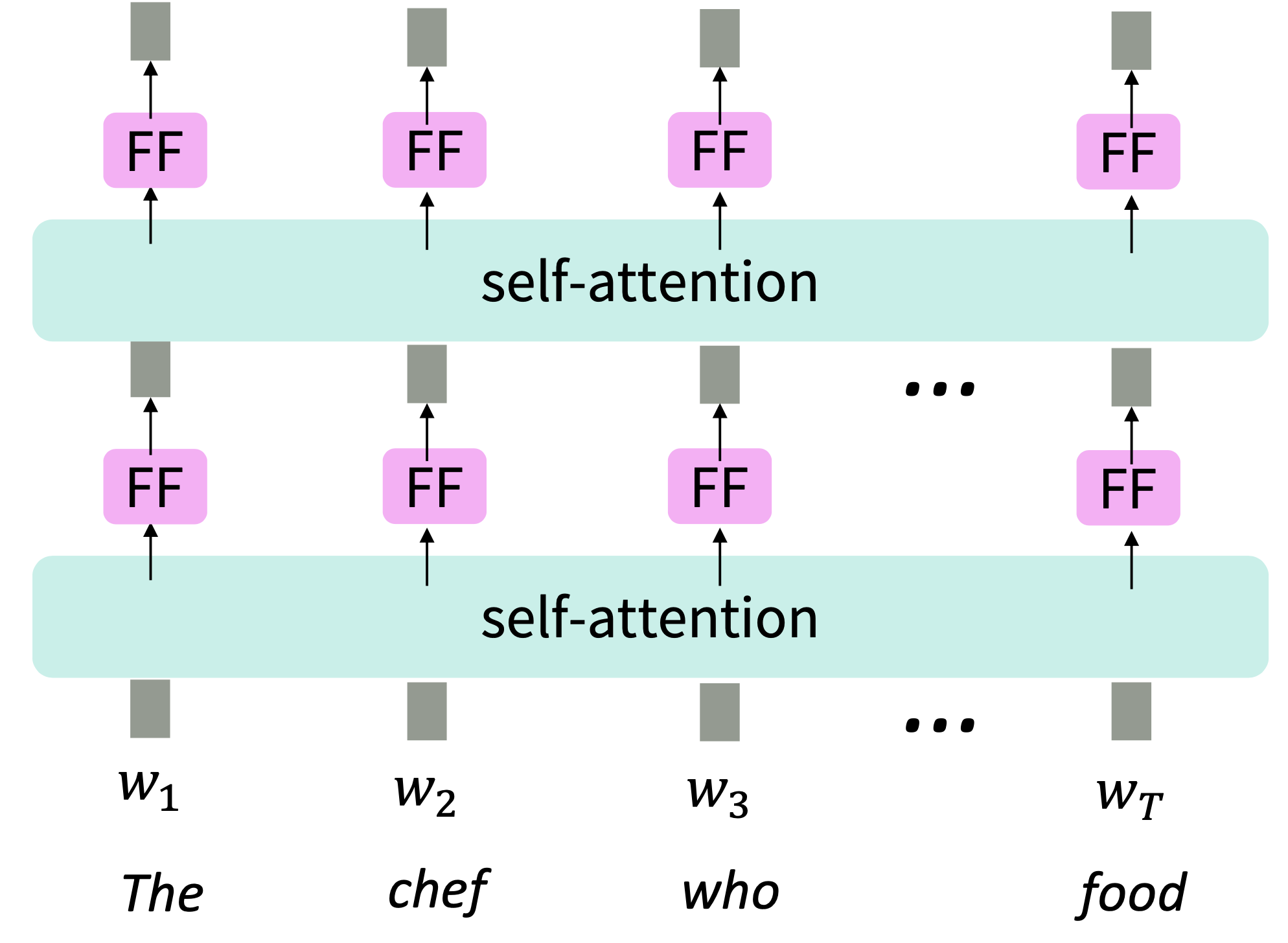
Reference. Stanford CS224n, 2021, Intuition: the FF network processes the result of attention

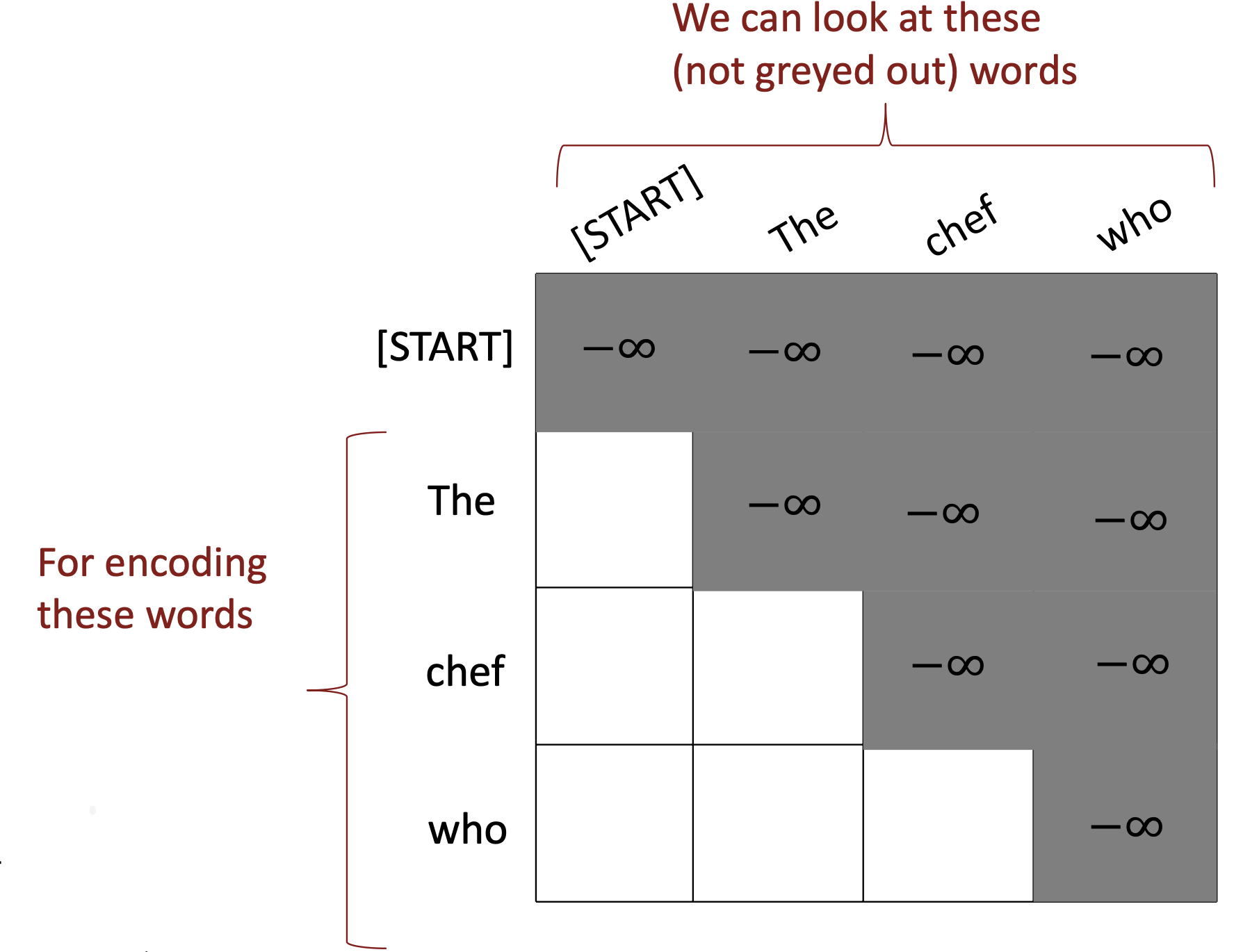
$\checkmark$ 3. Need to ensure we don’t “look at the future” when predicting a sequence → Mask out the future by artificially setting attention weights to 0

To use self-attention in  decoders , we need to ensure we can’t peek at the future. To enable parallelization, we  mask out attention  to future words by setting attention scores to −∞.

4. Transformer model

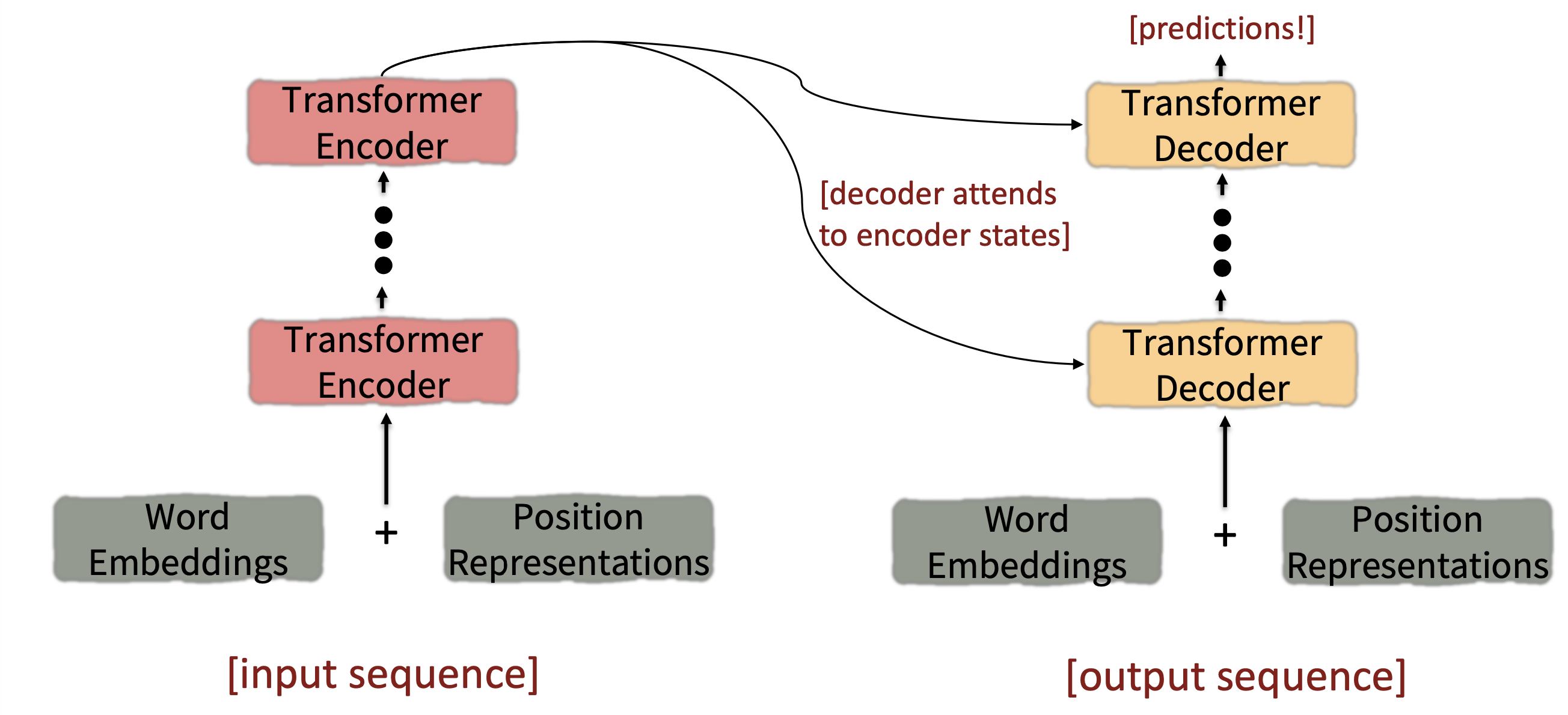
Reference. Stanford CS224n, 2021, The Transformer Encoder-Decoder [Vaswani et al., 2017]

4.1 Transformer Encoder

$\checkmark$ Key-query-value attention : How do we get the 𝑘, 𝑞, 𝑣 vectors from a single word embedding?

We saw that self-attention is when keys, queries, and values come from the same source. The Transformer does this in a particular way:

Then keys, queries, values are:

• These matrices allow  different aspects  of the 𝑥 vectors to be used/emphasized in each of the three roles.
• Let $𝑋 = [𝑥_1; … ; 𝑥_𝑇] \in \mathbb{R}^{𝑇\times 𝑑}$ be the concatenation of input vectors.
• First, note that $𝑋𝐾 \in \mathbb{R}^{𝑇\times 𝑑}, 𝑋𝑄 \in \mathbb{R}^{𝑇\times 𝑑}, 𝑋𝑉 \in \mathbb{R}^{𝑇\times 𝑑}.$
• The output is defined as $output = softmax(𝑋𝑄(𝑋𝐾)^⊤)\times 𝑋𝑉$

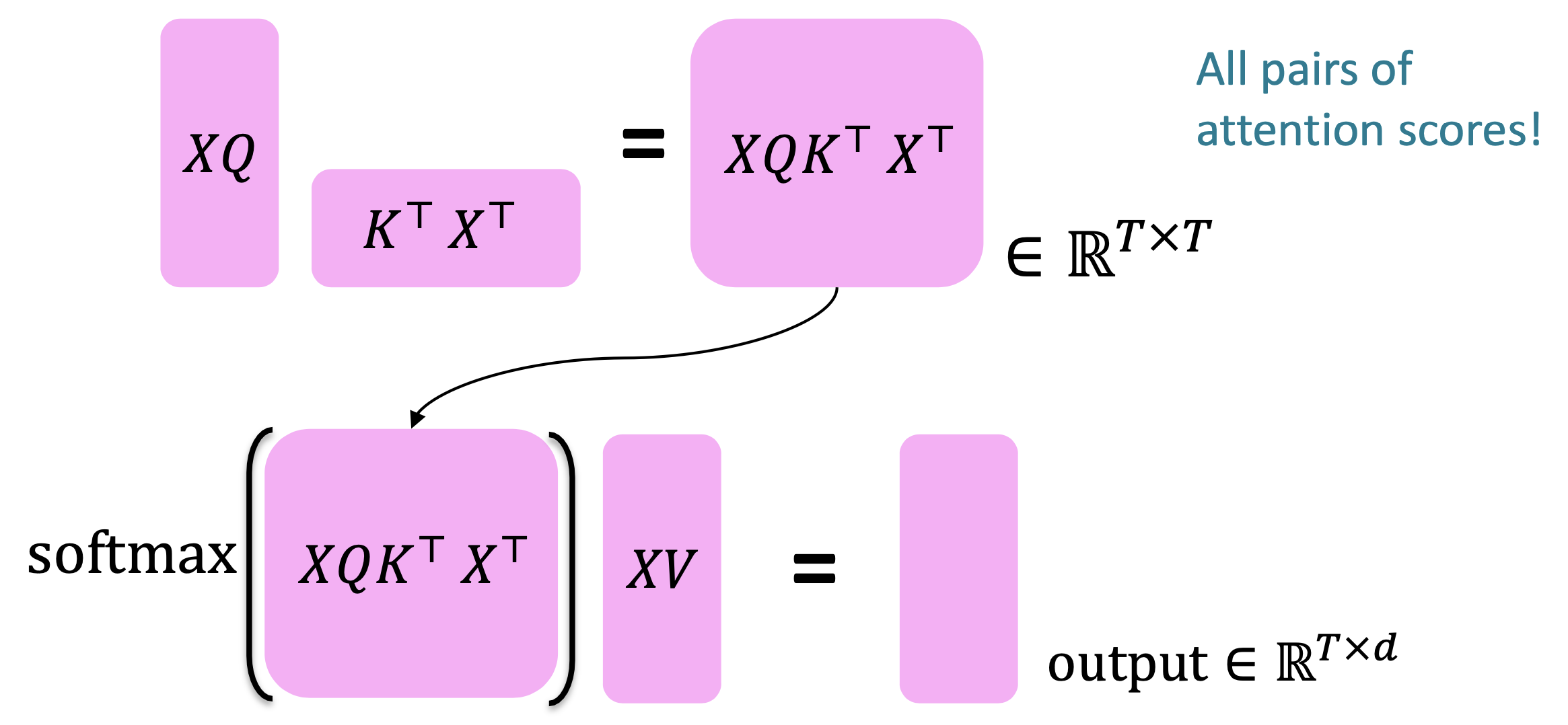
First, take the query-key dot products in one matrix multiplication: $𝑋𝑄(𝑋𝐾)^⊤$. Next, softmax, and compute the weighted average with another matrix multiplication.

$\checkmark$ Multi-headed attention : Attend to multiple places in a single layer!

• For word i, self-attention “looks” where $𝑥_i^⊤𝑄^⊤𝐾𝑥_j$  is high, but maybe we want to focus on different j for different reasons?
• We’ll define  multiple attention “heads”  through multiple Q,K,V matrices

Let, $Q_{\ell}, K_{\ell}, V_{\ell} \in \mathbb{R}^{d \times \frac{d}{h}}$, where h is the number of attention heads, and $\ell$ ranges from 1 to h.

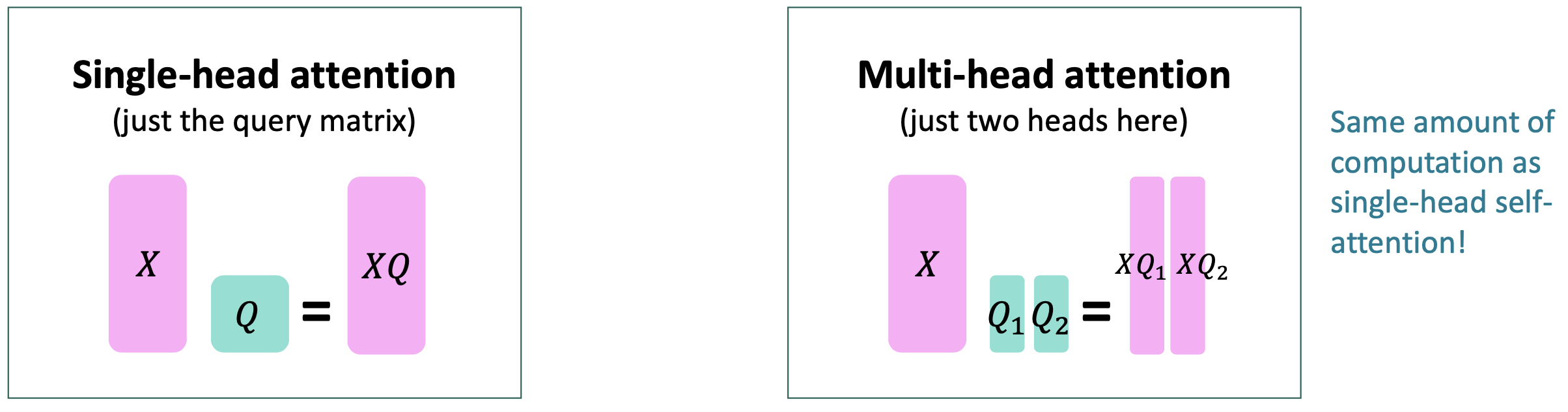
Each attention head performs attention independently:

Then the outputs of all the heads are combined!

• Each head gets to “look” at different things, and construct value vectors differently.

$\checkmark$ Tricks to help with training!

Residual connections, [ He et al., 2016 ]

Residual connections  are a trick to help models train better, Li et al., 2018

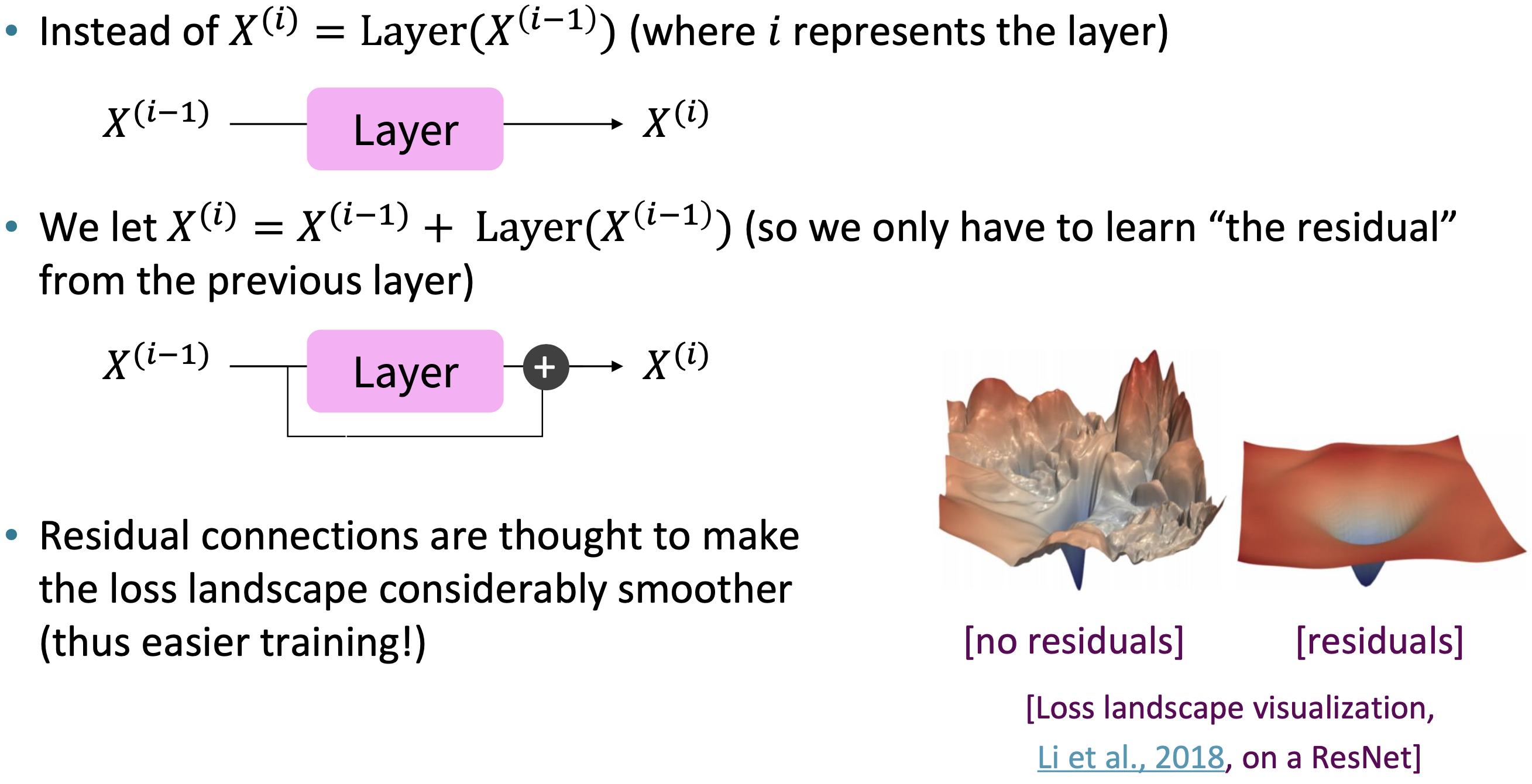
Reference. Stanford CS224n, 2021, Li et al., 2018

• Layer normalization  is a trick to help models train faster.
• Idea: cut down on uninformative variation in hidden vector values by normalizing to unit mean and standard deviation  within each layer .
• LayerNorm’s success may be due to its normalizing gradients [ Xu et al., 2019 ]

Then layer normalization computes:

Scaling the dot product

“Scaled Dot Product”  attention is a final variation to aid in Transformer training. When dimensionality 𝑑 becomes large, dot products between vectors tend to become large. Because of this, inputs to the softmax function can be large, making the gradients small.

Instead of the self-attention function we’ve seen:

We divide the attention scores by $\sqrt{d/h}$, to stop the scores from becoming large just as a function of $d/h$ (The dimensionality divided by the number of heads.)

• These tricks  don’t improve  what the model is able to do; they help improve the training process. Both of these types of modeling improvements are very important!

4.2 Transformer Encoder-Decoder

Looking back at the whole model, zooming in on an Encoder block:

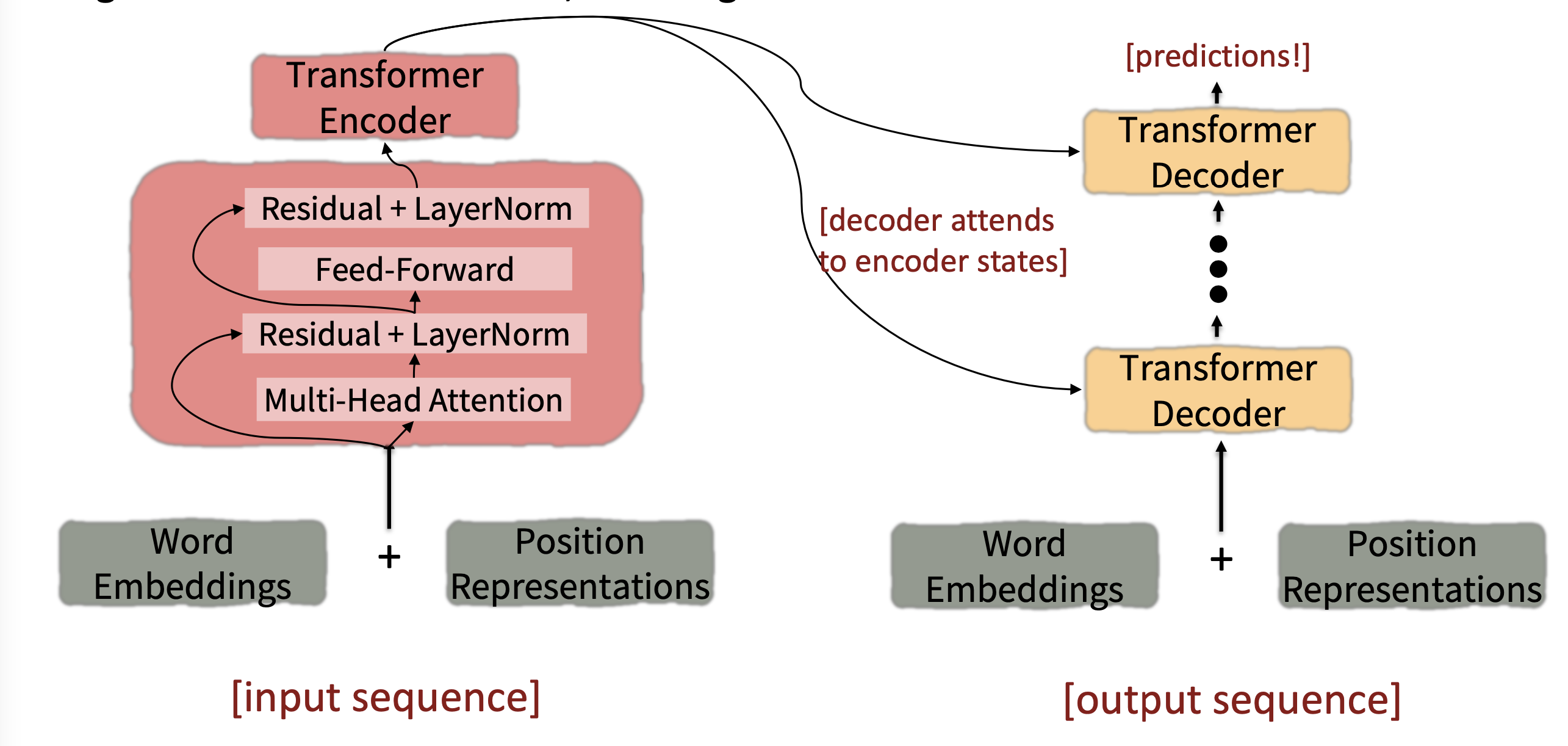
Reference. Stanford CS224n

Looking back at the whole model, zooming in on a Decoder block:

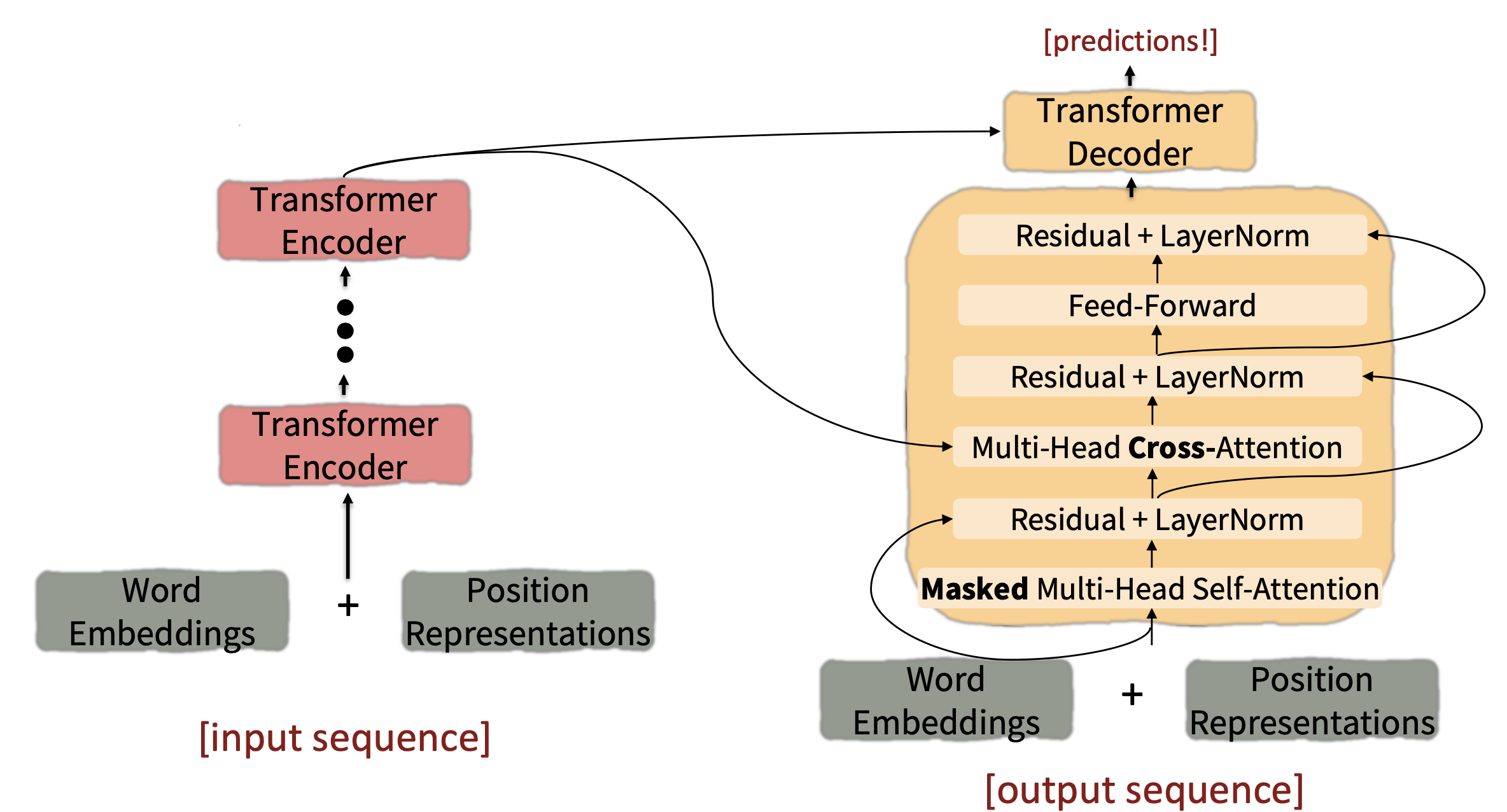
The only new part is attention from decoder to encoder(Multi-Head Cross-Attention and Residual+LayerNorm)

4.3 Cross-attention

• We saw that self-attention is when keys, queries, and values come from the same source.
• Let $h_1, \dots , h_𝑇$ be  output  vectors  from  the Transformer  encoder ; $𝑥_𝑖 \in \mathbb{R}^𝑑$
• Let $𝑧_1 , \dots , 𝑧_T$ be input vectors from the Transformer  decoder , $𝑧 \in \mathbb{R}^𝑑$

Then keys and values are drawn from the  encoder  (like a memory):

• And the queries are drawn from the  decoder, $q_i=Qz_i$

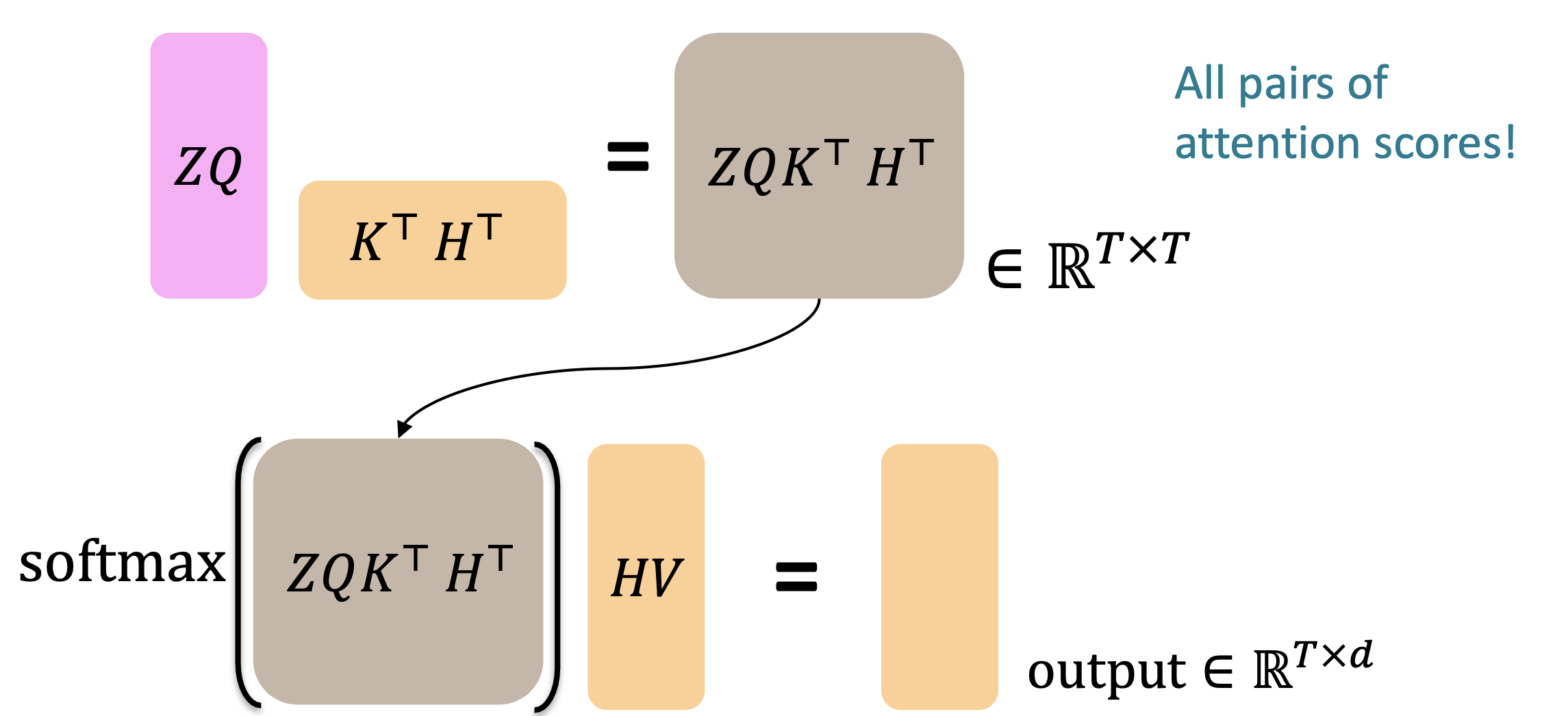
Let’s look at how cross-attention is computed, in matrices.

• First, take the query-key dot products in one matrix multiplication: $𝑍𝑄(𝐻𝐾)^⊤$. Next, softmax, and compute the weighted average with another matrix multiplication.

4.4 Recent work

• Computing all pairs of interactions means our computation grows quadratically  with the sequence length!
• For recurrent models, it only grew linearly!
• Position representations

Recent work on improving on quadratic self-attention cost

Considerable recent work has gone into the question,  Can we build models like Transformers without paying the $𝑂(𝑇^2)$   all-pairs self-attention cost?

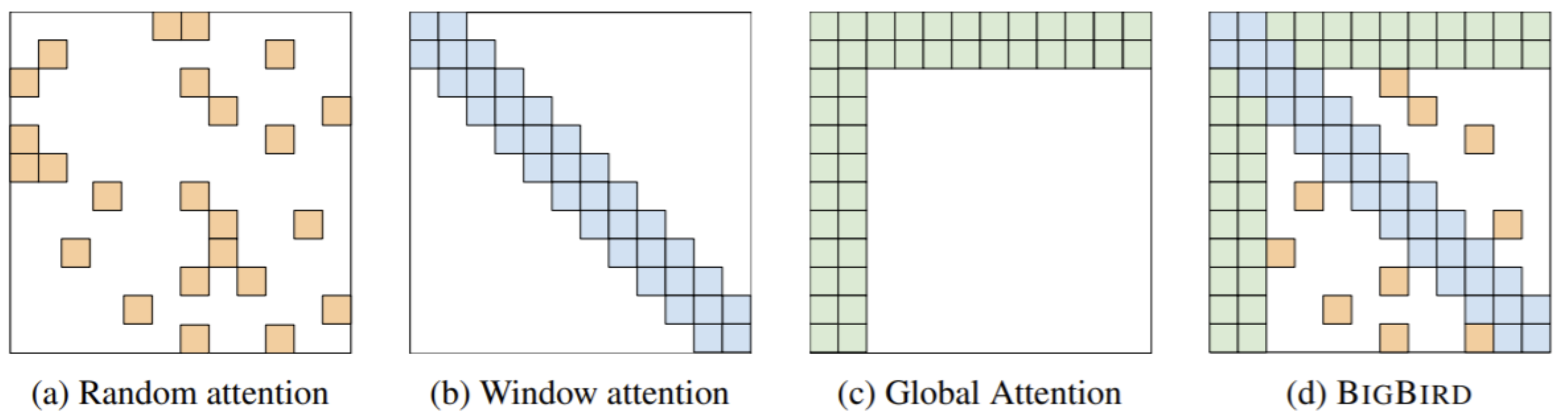
For example,  BigBird  [ Zaheer et al., 2021 ]

Key idea: replace all-pairs interactions with a family of other interactions,  like local windows ,  looking at everything , and  random interactions .

5. Pre-training

5.1 brief overview.

$\checkmark$ Word structure and subword models

Let’s take a look at the assumptions we’ve made about a language’s vocabulary. We assume a fixed vocab of tens of thousands of words, built from the training set. All  novel  words seen at test time are mapped to a single UNK.

Finite vocabulary assumptions make even  less  sense in many languages. Many languages exhibit complex  morphology , or word structure.

• The effect is more word types, each occurring fewer times.

Example: Swahili verbs can have hundreds of conjugations, each encoding a wide variety of information. (Tense, mood, definiteness, negation, information about the object, ++)

$\checkmark$ The byte-pair encoding algorithm

Subword modeling in NLP encompasses a wide range of methods for reasoning about structure below the word level. (Parts of words, characters, bytes.)

• The dominant modern paradigm is to learn a vocabulary of  parts of words (subword tokens).

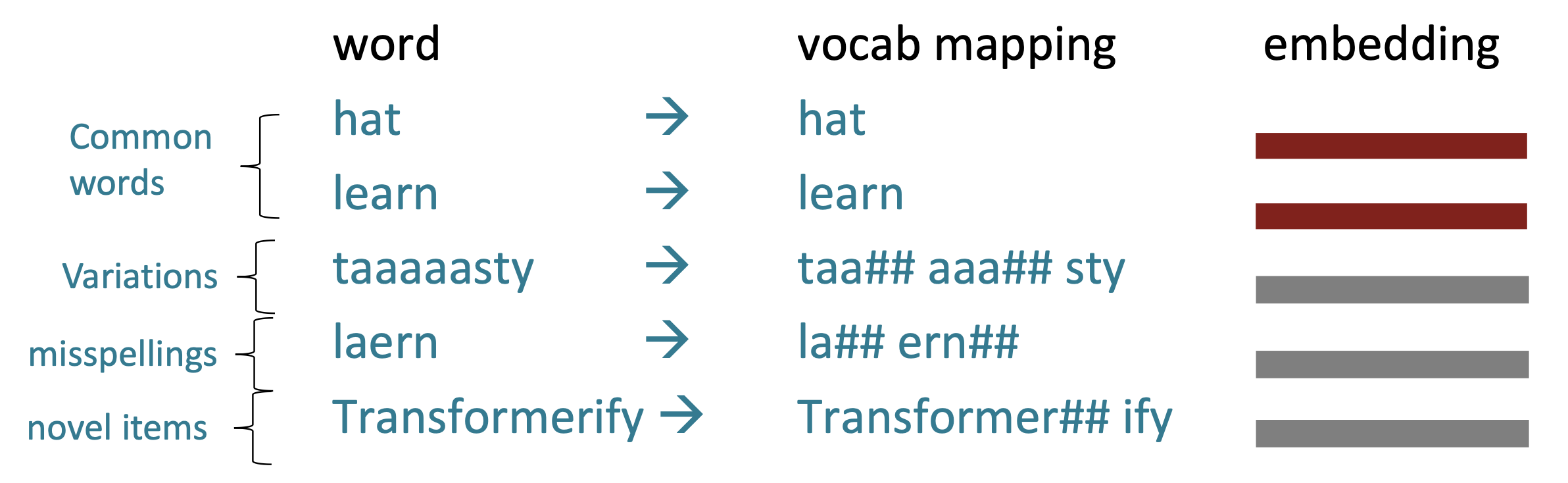
At training and testing time, each word is split into a sequence of known subwords.

Byte-pair encoding is a simple, effective strategy for defining a subword vocabulary.

• Start with a vocabulary containing only characters and an “end-of-word” symbol.
• Using a corpus of text, find the most common adjacent characters “a,b”; add “ab” as a subword.
• Replace instances of the character pair with the new subword; repeat until desired vocab size.

Originally used in NLP for machine translation; now a similar method (WordPiece) is used in pretrained models.

Common words end up being a part of the subword vocabulary, while rarer words are split into (sometimes intuitive, sometimes not) components.

In the worst case, words are split into as many subwords as they have characters.

$\checkmark$ Motivating model pretraining from word embeddings

Recall the adage we mentioned at the beginning of the course:

This quote is a summary of  distributional semantics , and motivated  word2vec . But:

Consider I  record  the  record *: the two instances of  record  mean different things.

$\checkmark$ Where we were: pretrained word embeddings, Circa 2017

• Start with pretrained word embeddings (no context!)
• Learn how to incorporate context in an LSTM or Transformer while training on the task.

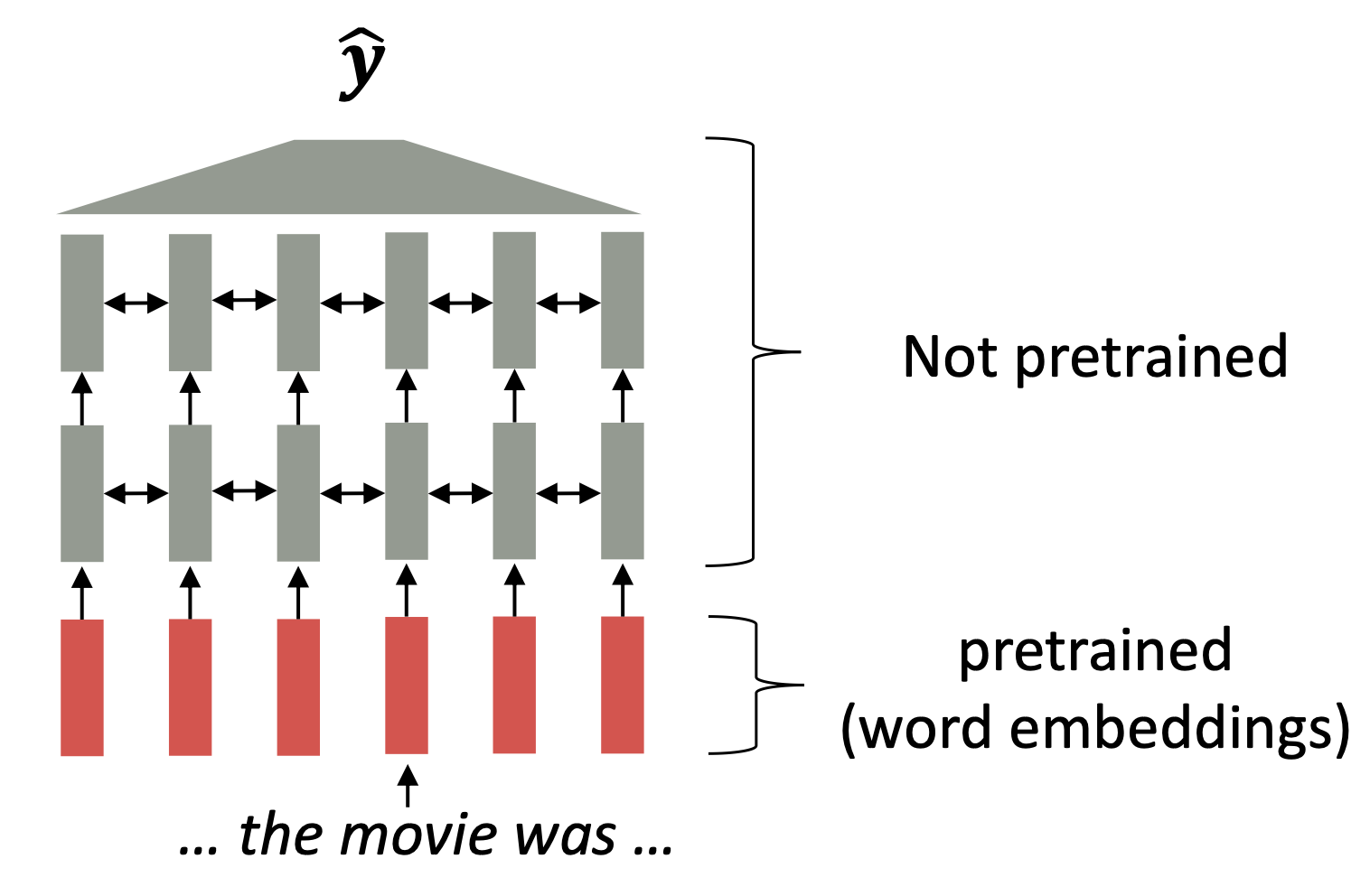
Reference. Stanford CS224n, Recall, movie gets the same word embedding, no matter what sentence it shows up in

$\checkmark$ Some issues to think about:

• The training data we have for our  downstream task  (like question answering) must be sufficient to teach all contextual aspects of language.
• Most of the parameters in our network are randomly initialized!

In modern NLP:

• All (or almost all) parameters in NLP networks are initialized via  pretraining .
• Pretraining methods hide parts of the input from the model, and train the model to reconstruct those parts.

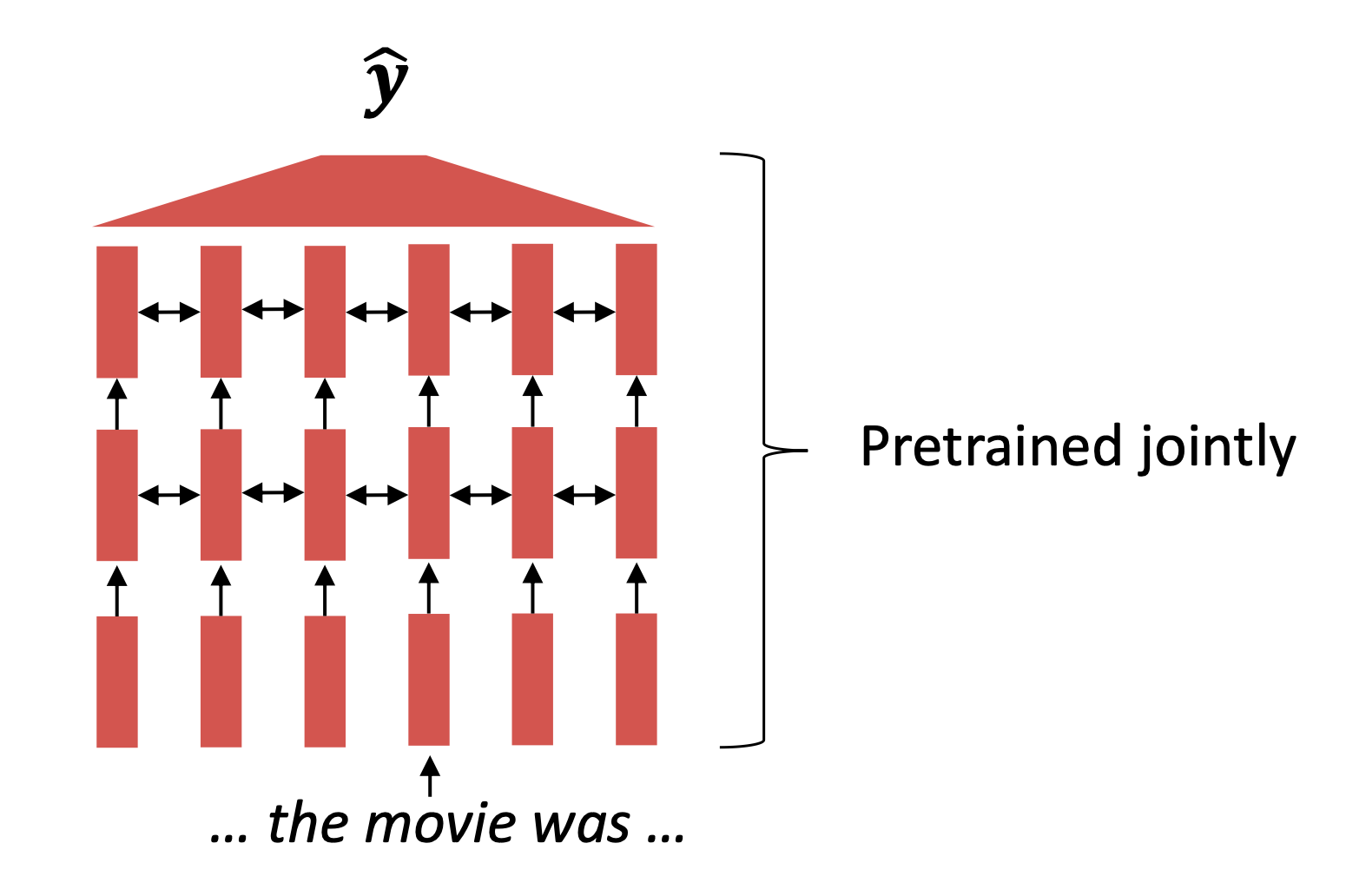
Reference. Stanford CS224n, This model has learned how to represent entire sentences through pretraining

• representations of language
• parameter initializations  for strong NLP models.
• Probability distributions  over language that we can sample from

Recall the  language modeling  task:

Model $p_{\theta}(w_t\lvert w_{1:t-1})$, the probability distribution over words given their past contexts.

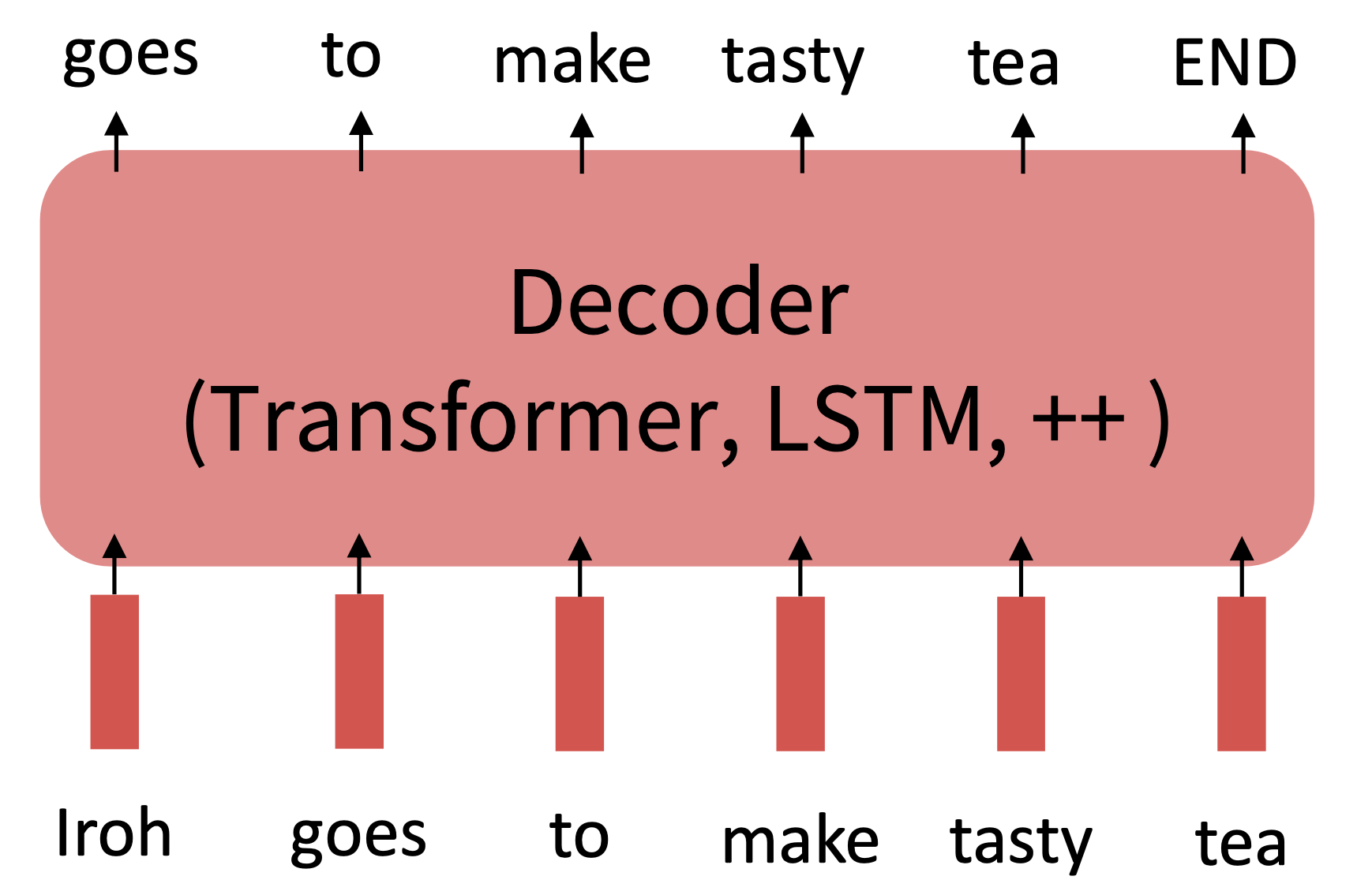
Reference. Stanford CS224n, Step 1: Pretrain (on language modeling)

$\checkmark$ Pretraining through language modeling [ Dai and Le, 2015 ]

• Train a neural network to perform language modeling on a large amount of text.
• Save the network parameters.

Pretraining can improve NLP applications by serving as parameter initialization.

Step 1: Pretrain (on language modeling): Lots of text; learn general things!

Step 2: Finetune (on your task) Not many labels; adapt to the task!

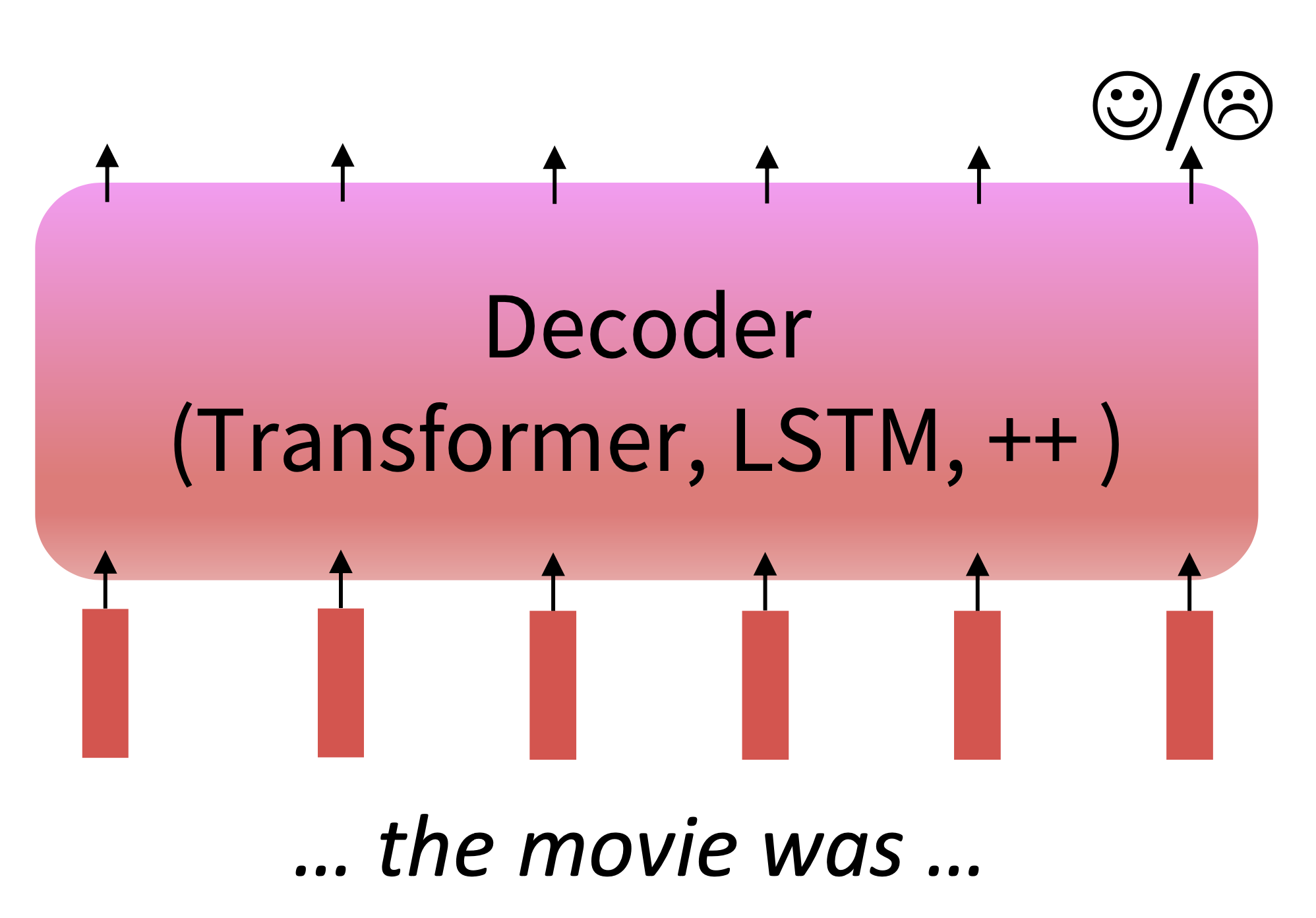
Why should pretraining and finetuning help, from a “training neural nets” perspective? Consider, provides parameters $\hat \theta$ by approximating $\underset{\theta}{min}\ L_{pretrain}(\theta)$, pretrain loss. Then, finetuning approximates $\underset{\theta}{min}\ L_{finetune}(\theta)$, starting at $\hat \theta$, finetuning loss. The pretraining may matter because stochastic gradient descent sticks (relatively) close to $\hat \theta$ during finetuning.

• So, maybe the finetuning local minima near $\hat \theta$ tend to generalize well!
• And/or, maybe the gradients of finetuning loss near $\hat \theta$ propagate nicely!

5.2 Model Pretraining ways

$\checkmark$ #1 Decoders

Pretraining

When using language model pretrained decoders, we can ignore that they were trained to model $p(w_t\lvert w_{1:t-1})$. We can fine-tune them by training a classifier on the lsat word’s hidden state.

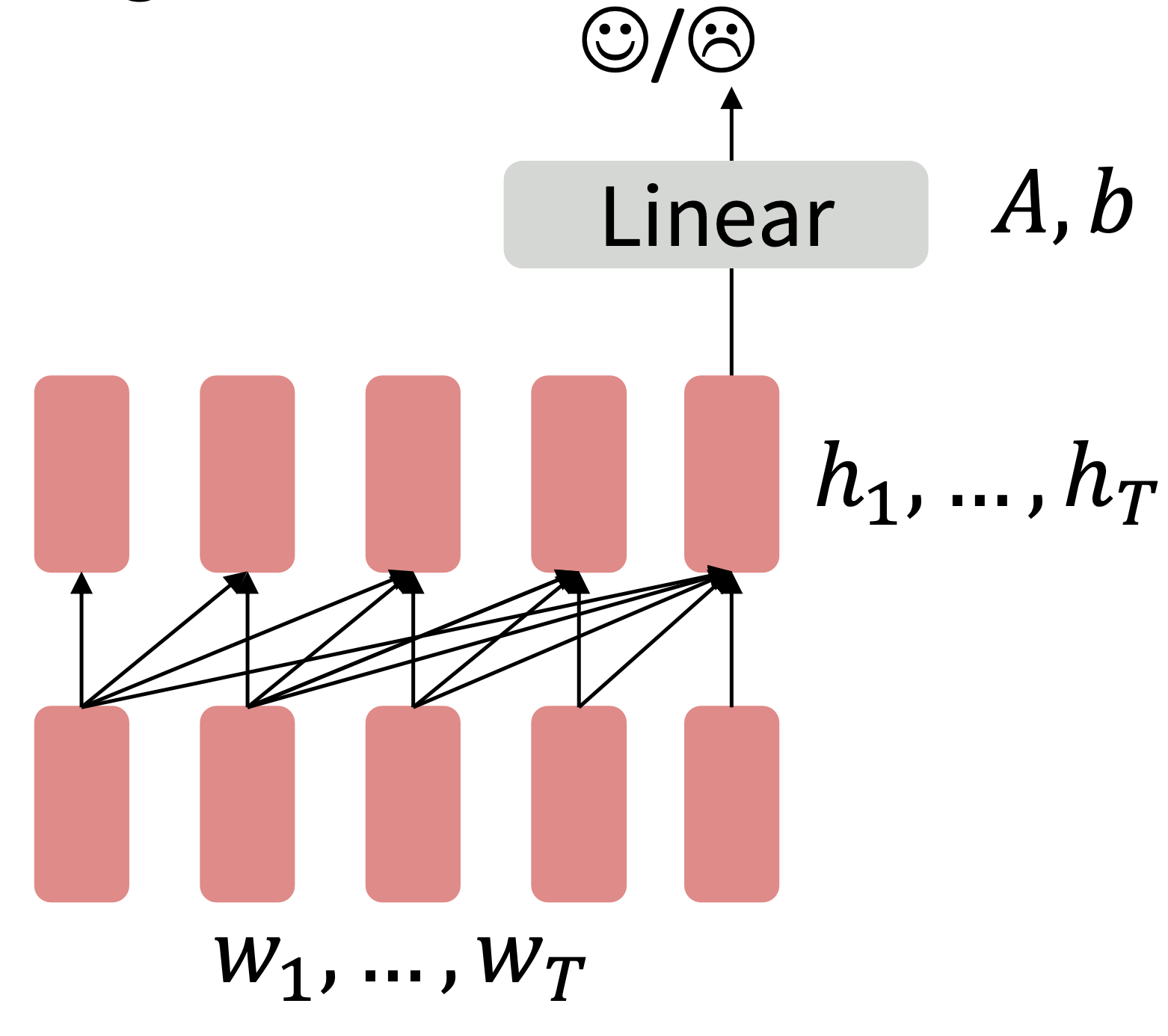
Reference. Stanford CS224n, 2021, Note how the linear layer hasn’t been pretrained and must be learned from scratch.

Where A and b are randomly initialized and specified by the downstream task. Gradients backpropagate through the whole network.

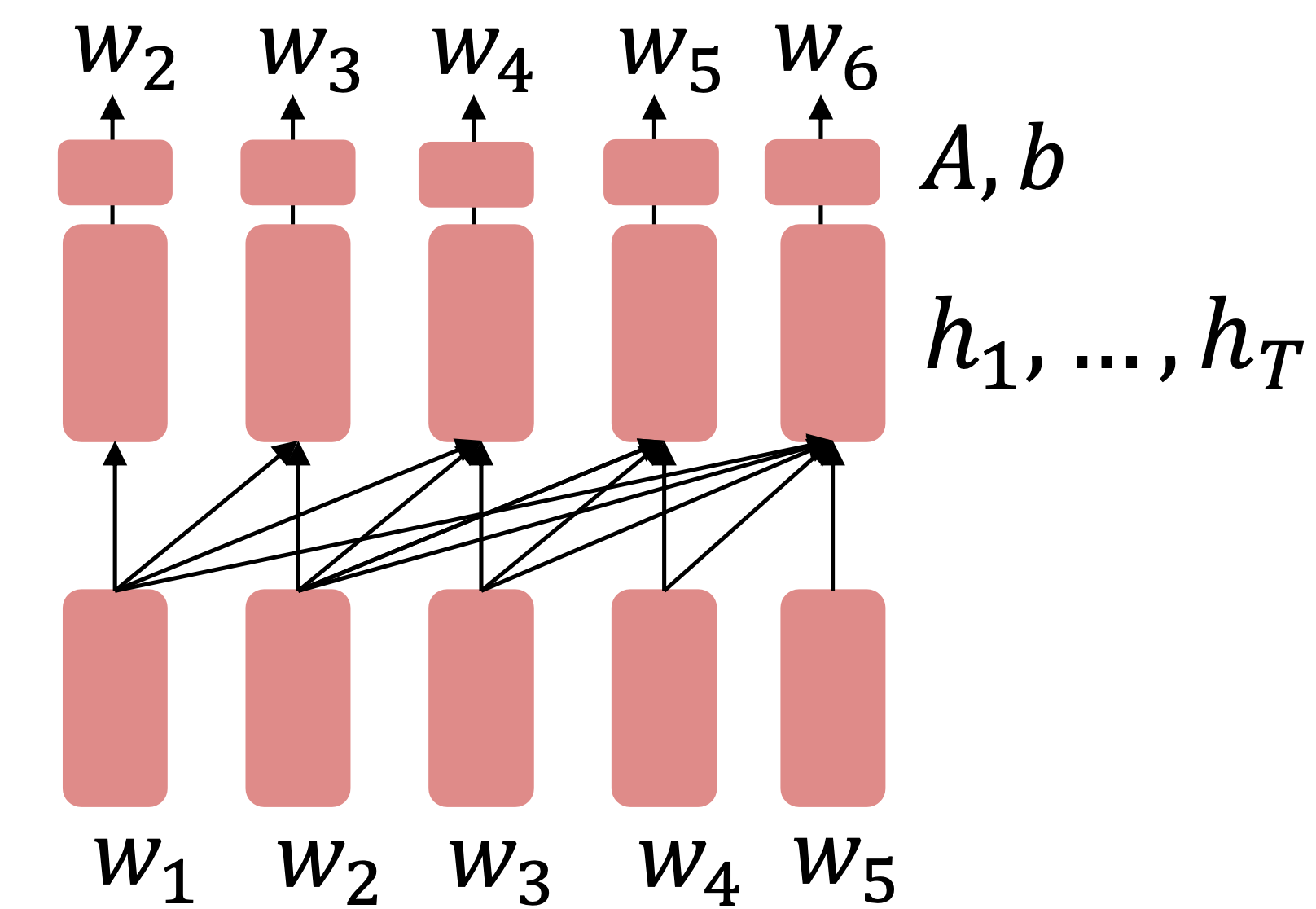
Reference. Stanford CS224n, 2021, Note how the linear layer has been pretrained.

It’s natural to pretrain decoders as language models and then use them as generators, finetuning their $p_{\theta}(w_t\lvert w_{1:t-1})$.

This is helpful in tasks  where the output is a sequence  with a vocabulary like that at pretraining time.

• Dialogue (context=dialogue history)
• Summarization (context=document)

Where A, b were pretrained in the language model

$\checkmark$ Generative Pretrained Transformer (GPT) [Radford et al., 2018]

2018’s GPT was a big success in pretraining a decoder!

• Transformer decoder with 12 layers.
• 768-dimensional hidden states, 3072-dimensional feed-forward hidden layers.
• Byte-pair encoding with 40,000 merges

Trained on BooksCorpus: over 7000 unique books.

• Contains long spans of contiguous text, for learning long-distance dependencies.
• The acronym “GPT” never showed up in the original paper; it could stand for “Generative PreTraining” or “Generative PreTrained Transformer”

How do we format inputs to our decoder for  finetuning tasks?

Radford et al., 2018 evaluate on natural language inference.

Natural Language Inference: Label pairs of sentences as entailing/contradictory/neutral

Here’s roughly how the input was formatted, as a sequence of tokens for the decoder.

The linear classifier is applied to the representation of the [EXTRACT] token.

Increasingly convincing generations (GPT2) [ Radford et al., 2018 ]

We mentioned how pretrained decoders can be used  in their capacities as language models.

GPT-2,  a larger version of GPT trained on more data, was shown to produce relatively convincing samples of natural language.

$\checkmark$ #2 Encoders, Encoders get bidirectional context!

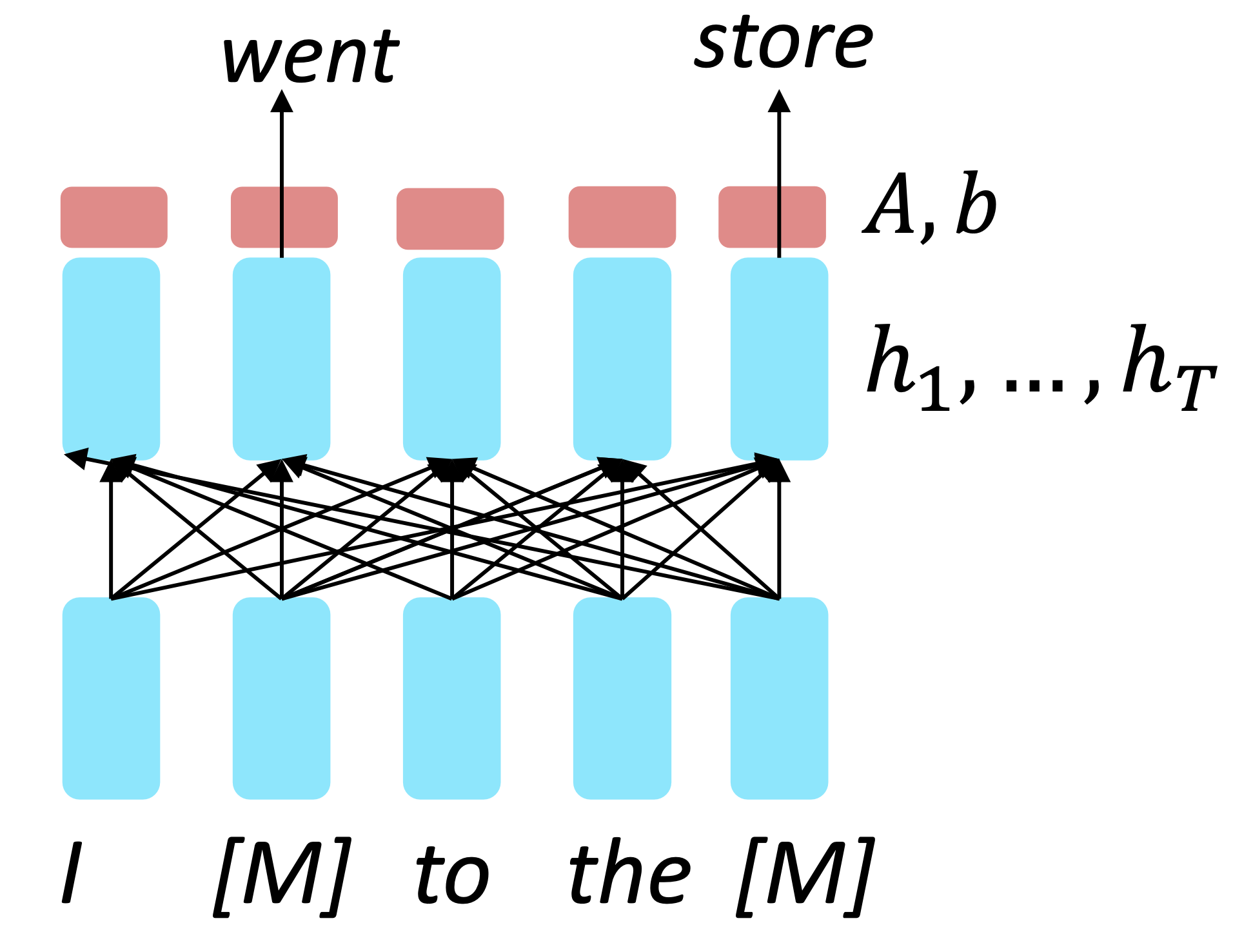
Reference. Devlin et al., 2018

Idea: replace some fraction of words in the input with a special [MASK] token ; predict these words.

Only add loss terms from words that are “masked out.” If $\tilde x$ is the masked version of x, we’re learning $p_{\theta}(x\lvert \tilde x)$. Called  Masked LM .

$\checkmark$ BERT: Bidirectional Encoder Represetations from Transformers

Devlin et al., 2018 proposed the “Masked LM” objective and  released the weights of a pretrained Transformer , a model they labeled BERT.

Some more details about Masked LM for BERT:

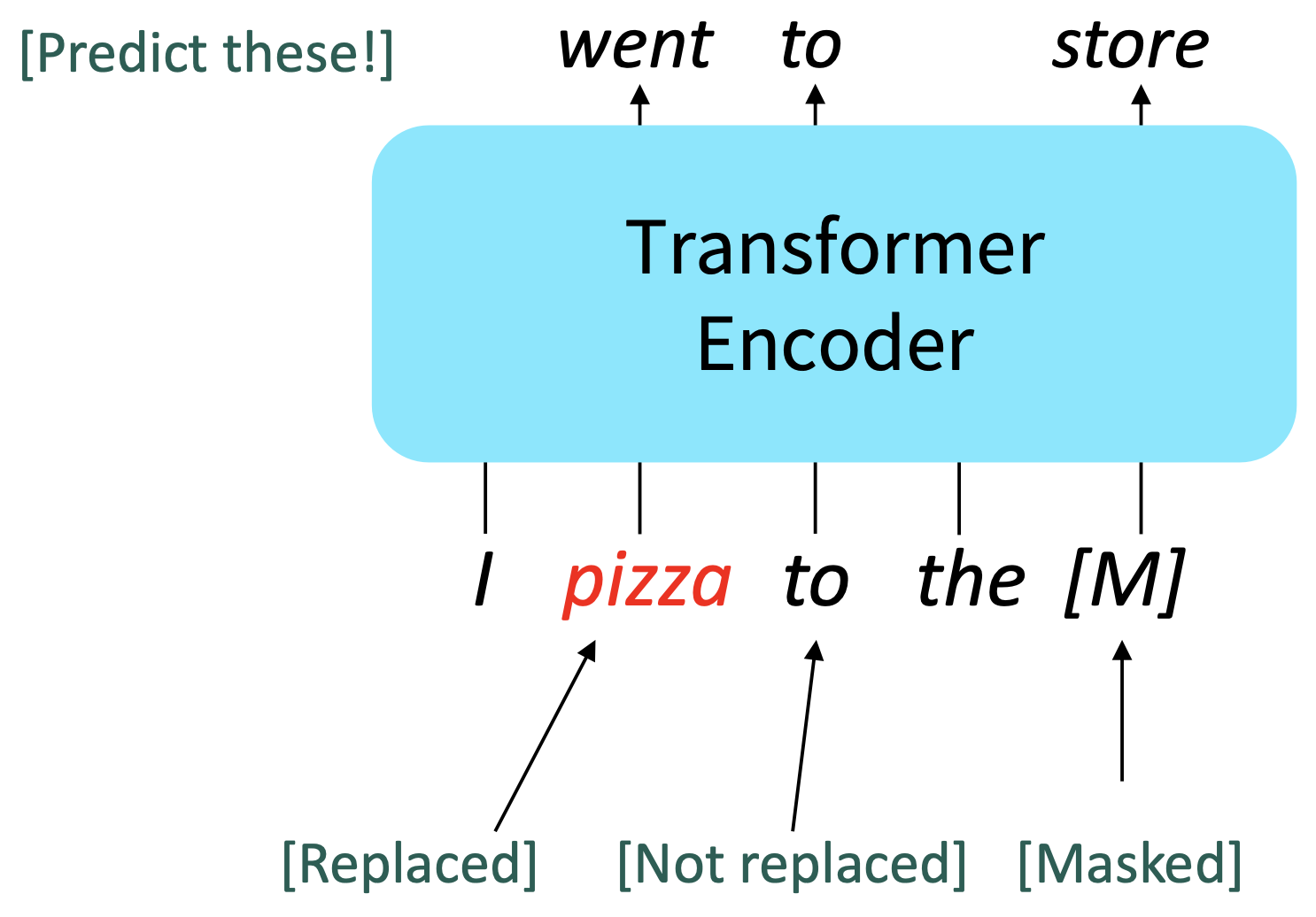
• Replace input word with [MASK] 80% of the time
• Replace input word with a random token 10% of the time
• Leave input word unchanged 10% of the time (but still predict it!)
• Why? Doesn’t let the model get complacent and not build strong representations of non-masked words. (No masks are seen at fine-tuning time!)

The Pretraining input to BERT was two separate contiguous chunks of text: “Segment Embedding”, Devlin et al., 2018 ,  Liu et al., 2019 ]

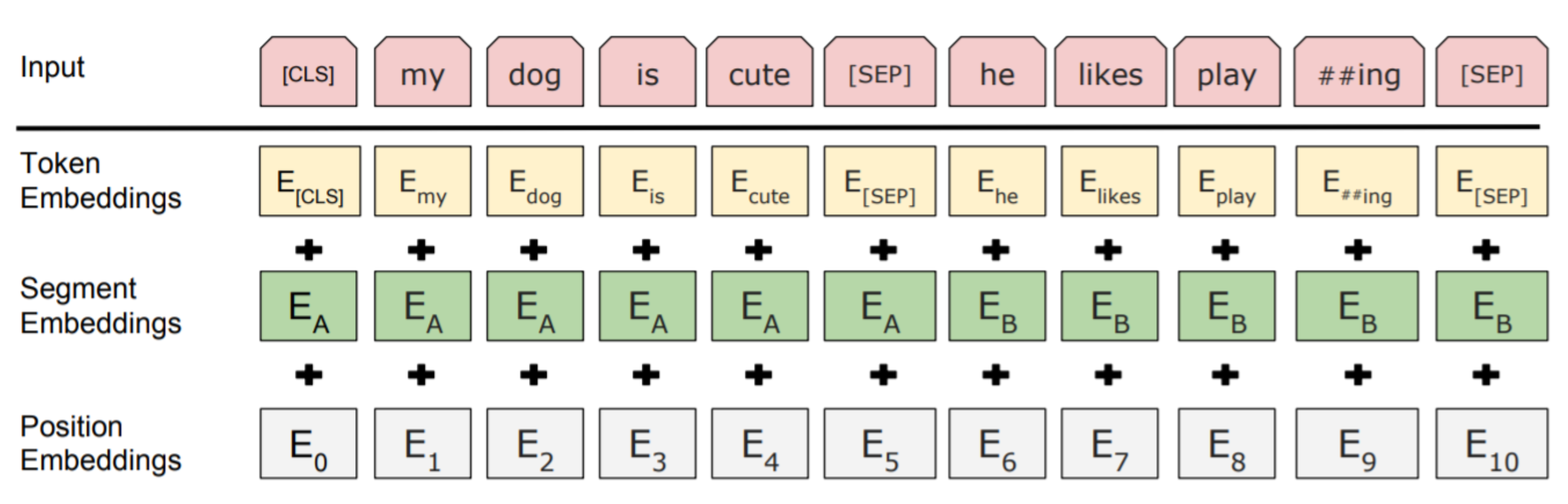
Reference. Devlin et al., 2018, Liu et al., 2019

BERT was trained to predict whether one chunk follows the other or is randomly sampled. Later work has argued this “next sentence prediction” is not necessary.

Two models were released:

BERT-base: 12 layers, 768-dim hidden states, 12 attention heads, 110 million params

BERT-large: 24 layers, 1024-dim hidden states, 16 attention heads, 340 million params.

Trained on:

BooksCorpus (800 million words)

English Wikipedia (2,500 million words)

Pretraining is expensive and impractical on a single GPU.

BERT was pretrained with 64 TPU chips for a total of 4 days. 

TPUs are special tensor operation acceleration hardware)

Finetuning is practical and common on a single GPU

“Pretrain once, finetune many times.”

• QQP:  Quora Question Pairs (detect paraphrase • questions)
• QNLI : natural language inference over question answering data
• SST-2 : sentiment analysis
• CoLA : corpus of linguistic acceptability (detect whether sentences are grammatical.)
• STS-B : semantic textual similarity
• MRPC : microsoft paraphrase corpus
• RTE : a small natural language inference corpus

If your task involves generating sequences, consider using a pretrained decoder; BERT and other pretrained encoders don’t naturally lead to nice autoregressive (1-word-at-a-time) generation methods.

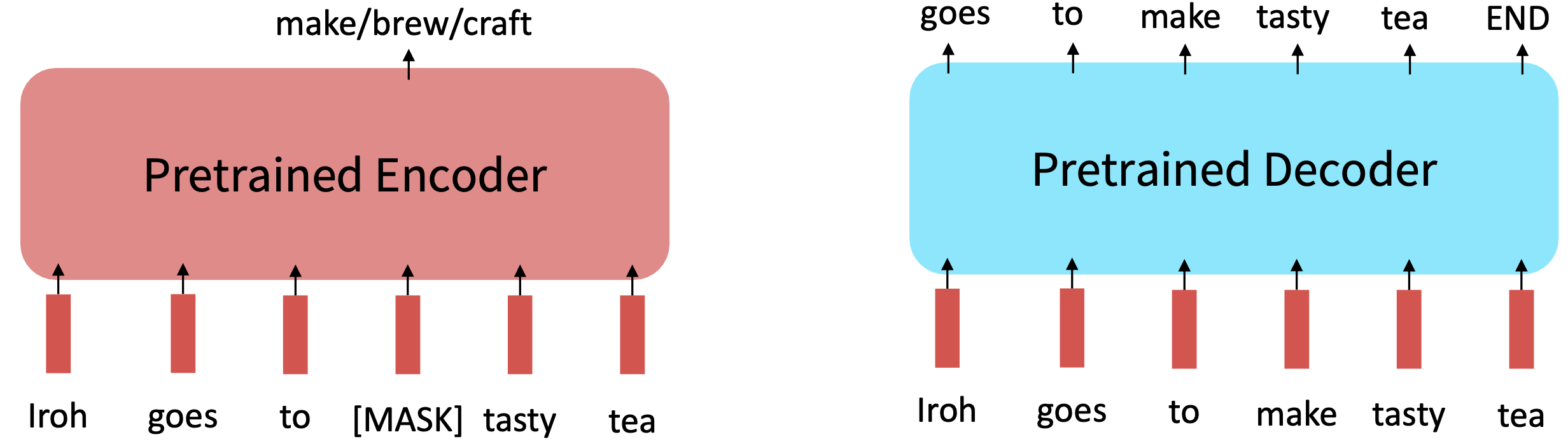
Expansions of BERT

RoBERTa, SpanBERT, +++

RoBERTa: mainly just train BERT for longer and remove next sentence prediction!, Liu et al., 2019

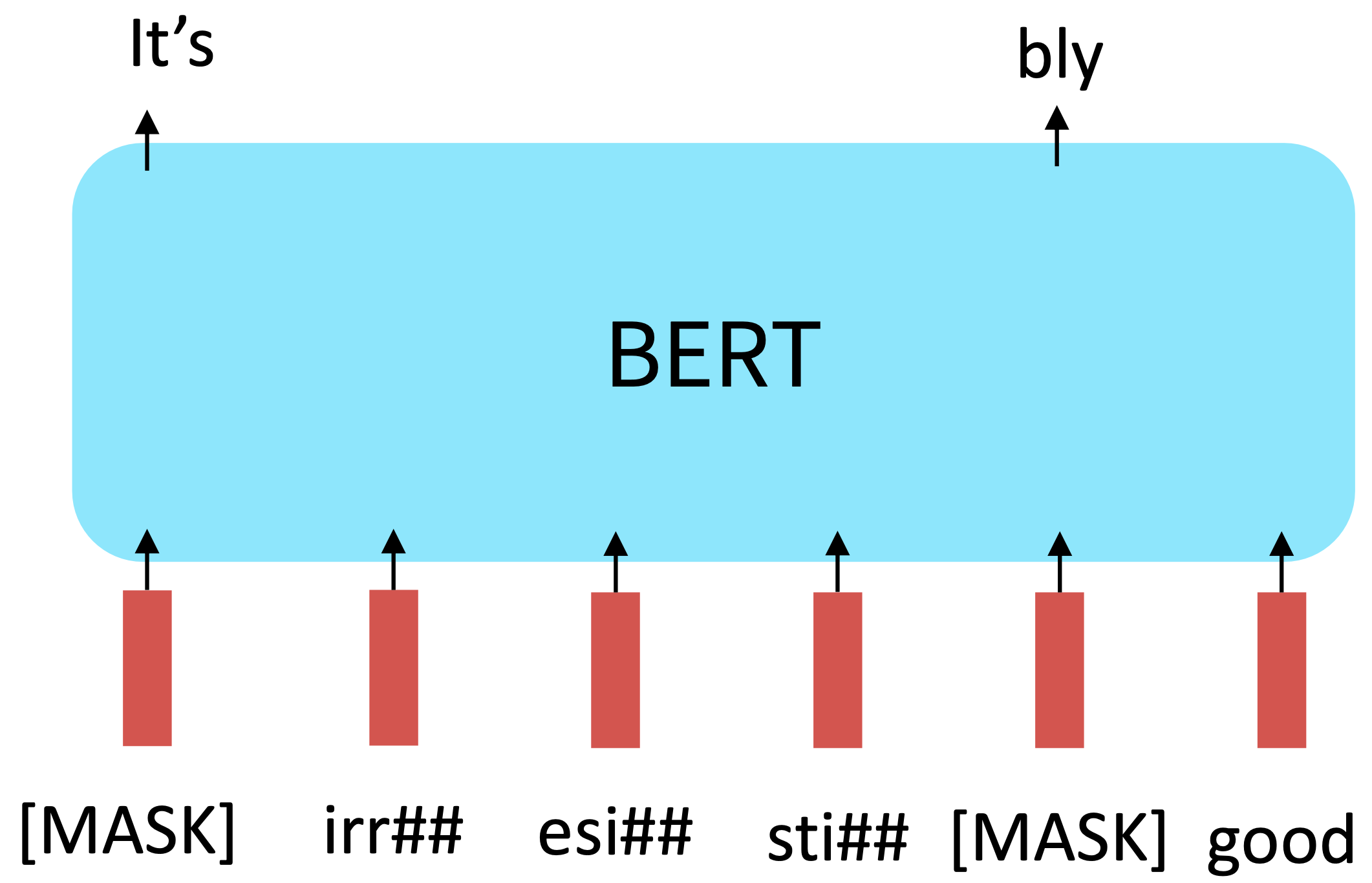
Reference. Liu et al., 2019

SpanBERT: masking contiguous spans of words makes a harder, more useful pretraining task, Joshi et al., 2020

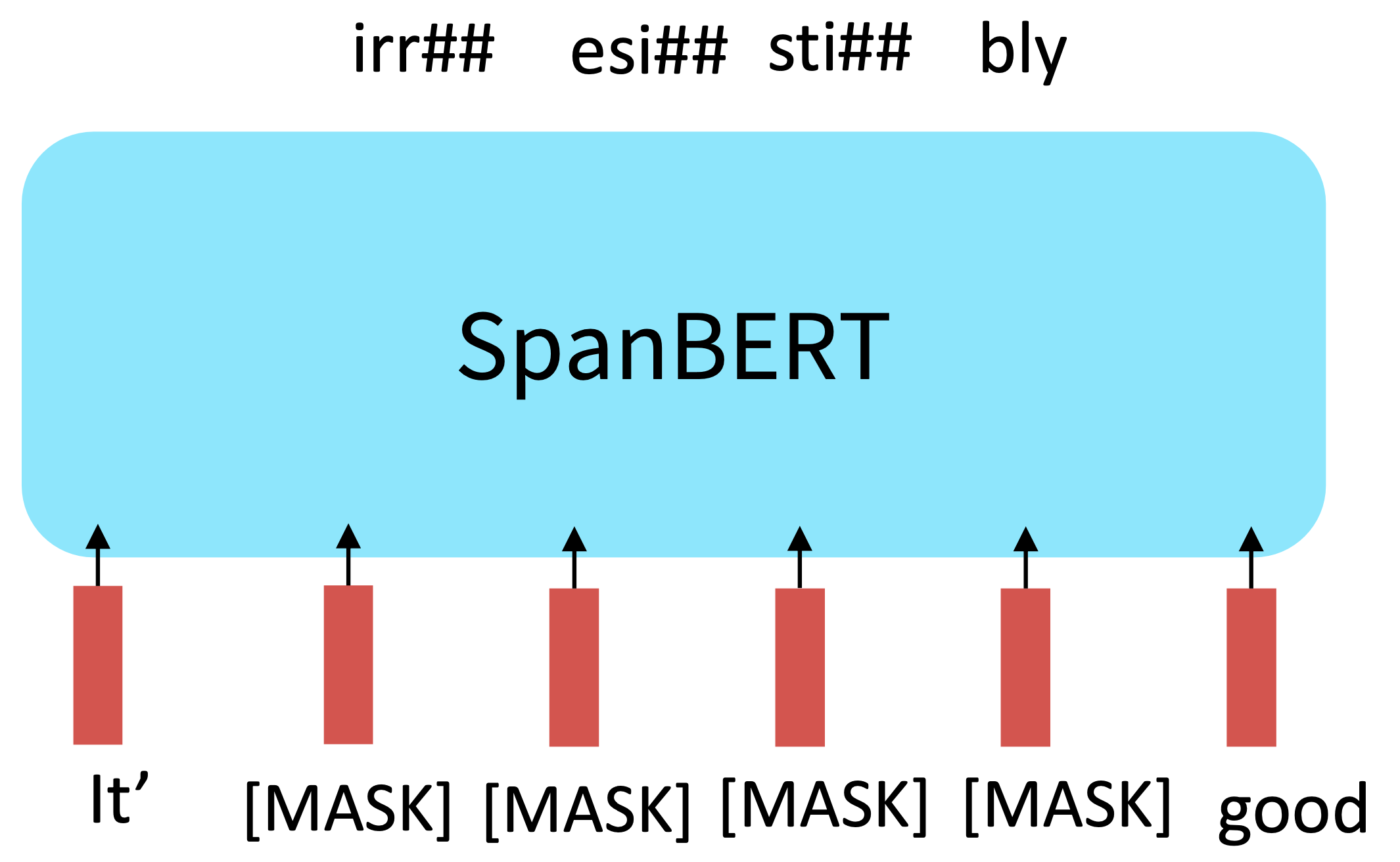
Reference. Joshi et al., 2020

$\checkmark$#3 Encoder-Decoders

For  encoder-decoders , we could do something like  language modeling , but where a prefix of every input is provided to the encoder and is not predicted.

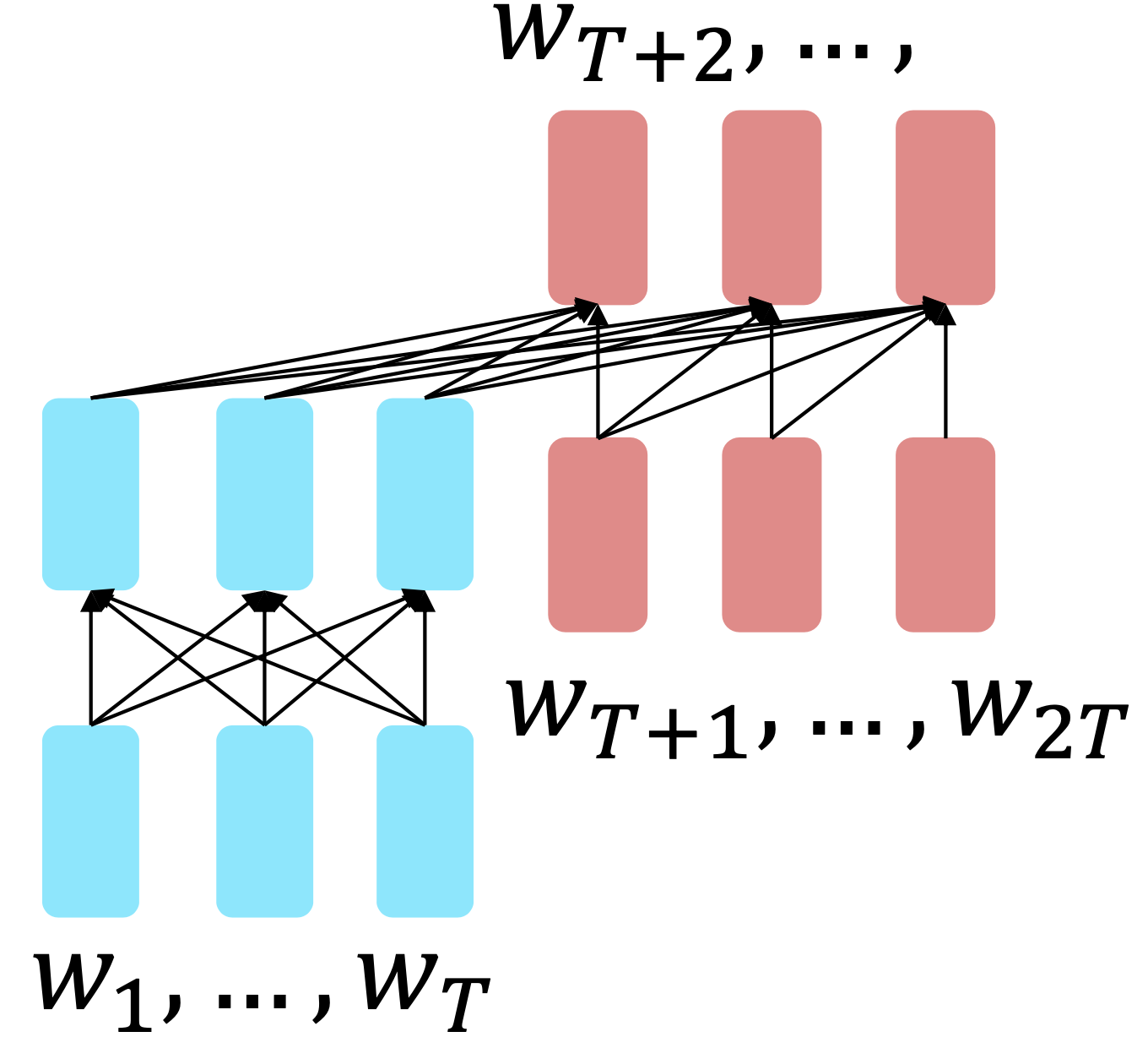
Reference. Raffel et al., 2018

The  encoder  portion benefits from bidirectional context; the  decoder  portion is used to train the whole model through language modeling.

What  Raffel et al., 2018  found to work best was  span corruption.  Their model:  T5 , which replaces different-length spans from the input with unique placeholders; decode out the spans that were removed

This is implemented in text preprocessing: it’s still an objective that looks like  language modeling  at the decoder side.

A fascinating property of T5: it can be finetuned to answer a wide range of questions, retrieving knowledge from its parameters.

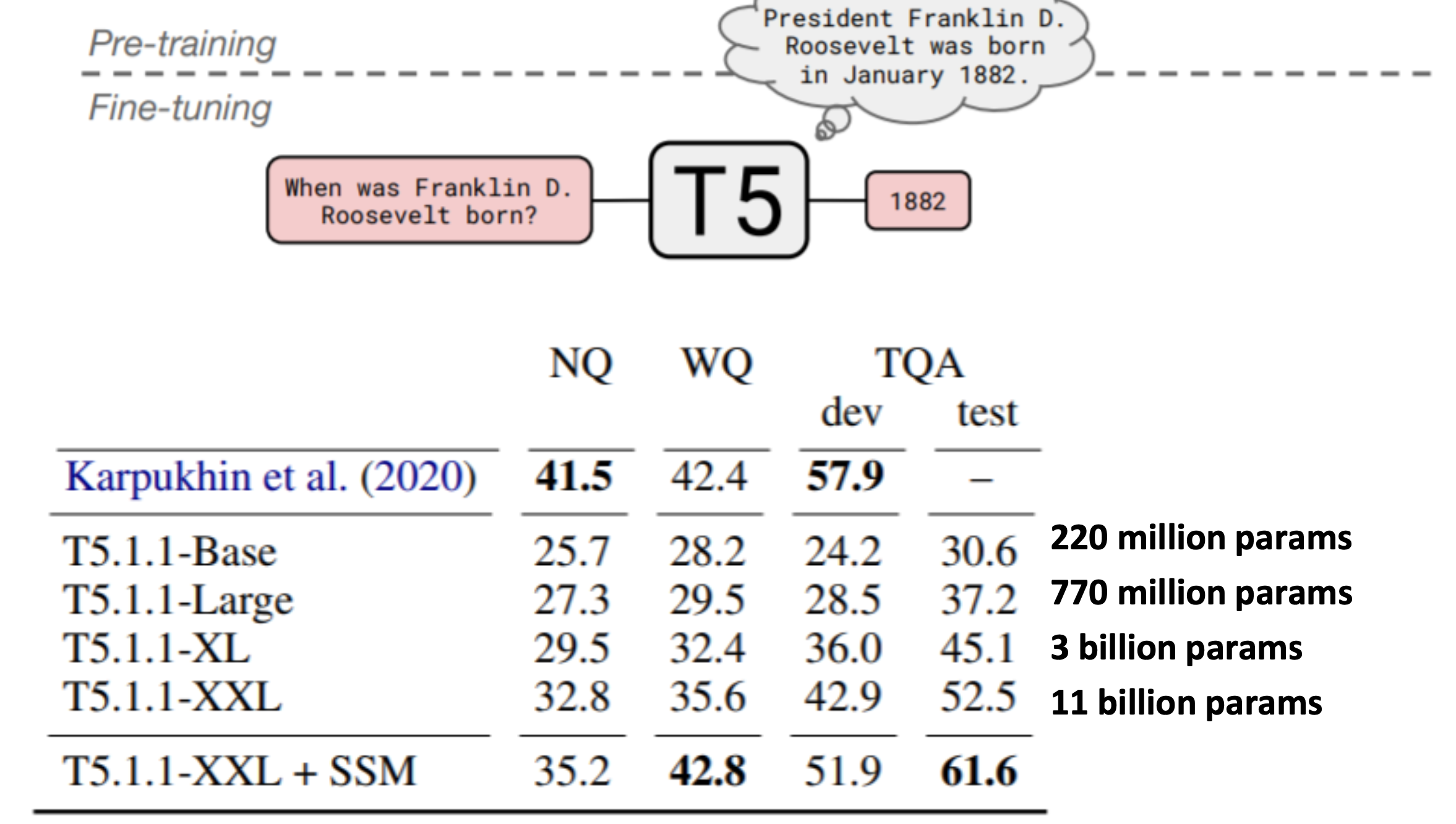
Reference. Raffel et al., 2018, NQ: Natural Questions, WQ: WebQuestions, TQA: Trivia QA, All "open-domain" versions

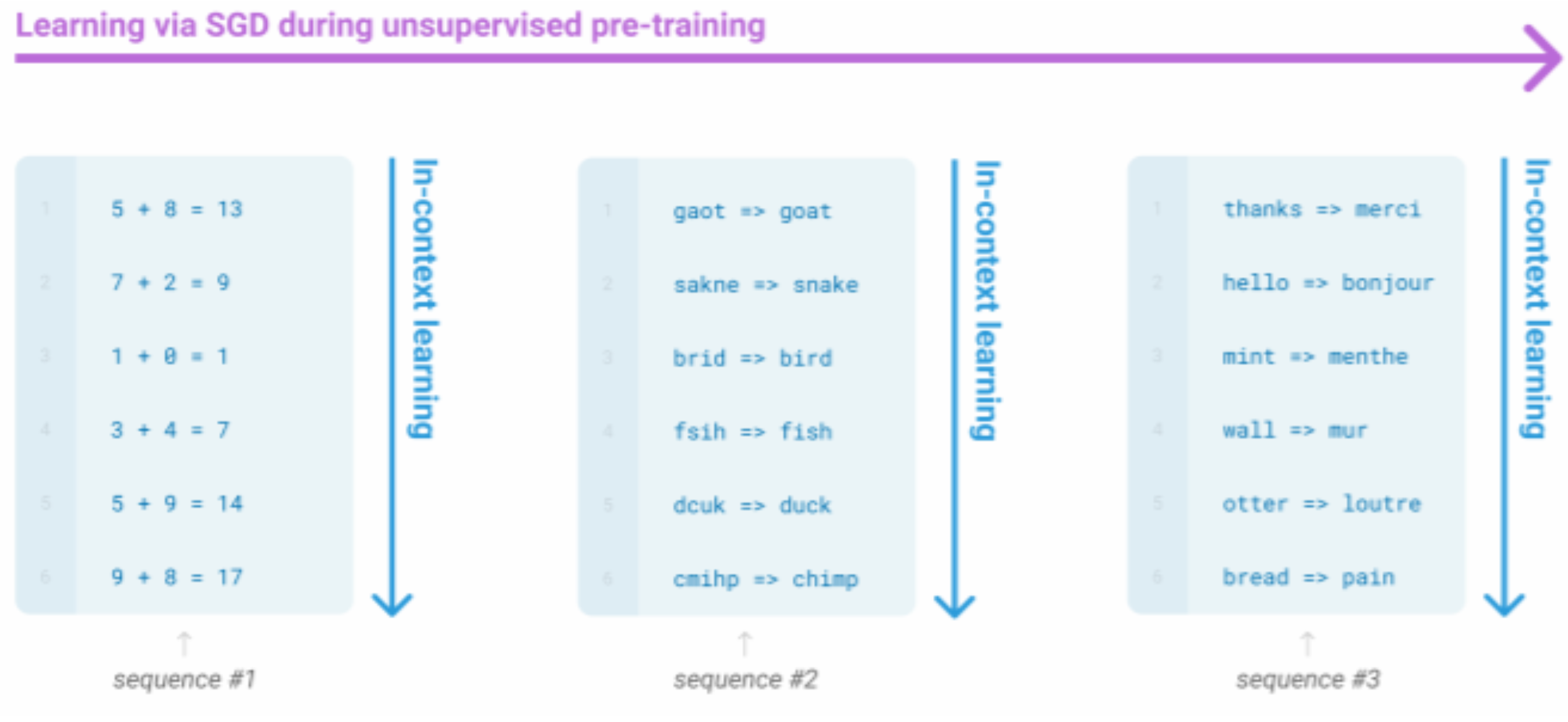
6. GPT-3, In-context learning, and very large models

Very large language models seem to perform some kind of learning without gradient steps simply from examples you provide within their contexts. GPT-3 is the canonical example of this. The largest T5 model had 11 billion parameters. GPT-3 has 175 billion parameters.

The in-context examples seem to specify the task to be performed, and the conditional distribution mocks performing the task to a certain extent.

Input (prefix within a single Transformer decoder context):

Output (conditional generations):

Very large language models seem to perform some kind of learning  without gradient steps  simply from examples you provide within their contexts.