flow rate experiment conclusion

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

Lab Example 1 - Lab Report

Introduction to engineering (engr a110), orange coast college, students also viewed.

• HW2, Theromodynamic - Engineering Exam.
• Cheat Sheet for Chapter 6 - Propositional Logic
• Final Exam , Thermodynamic
• EGME 304-01 Summer 2021 Final Exam
• Solution For Exercise 8-3 Stop and Assess Yourself

Related documents

• Critical Thinking Review Topics for Quiz One.docx
• 2 Chronicles 1 - Minh Tuong
• Mech of ev - Mechanisms of evolution
• Hw2 - Find the limit and instantaneous rate of change

Preview text

Flow Through a Venturi Meter EGME 306B

Fluids and Thermal Laboratory

March 2, 2018

Table of Contents

Abstract................................................................................................................ List of Symbols and Units.......................................................................................... Theory................................................................................................................. Procedure and Experimental Setup................................................................................ Sample Calculation and Error Analysis........................................................................... Results................................................................................................................ Discussion and Conclusion........................................................................................ References........................................................................................................... Appendix............................................................................................................

List of Symbols and Units

Symbol Name of Variable Units

DD Diameter of the throat m

DA Diameter of the inlet m

hA-hD Height difference between inlet and throat

Qact Volumetric Flow rate from experiment

Qtheo Volumetric Theoretical flow rate

Re Reynolds number No units

HT Head loss m

Cd Discharge coefficient No units

μ Viscosity N*s/m 2

ρ Density of water kg/m 3

g Gravity m/s 2

p Pressure N/m 2 or Pa

Mass flow rate kg/s

Venturi meters are instruments of measurements that use a pipe with a throat, which is much narrower from the inlet of the pipe to increase the flow velocity and a pressure drop can be calculated using that flow velocity. This can be seen in figure I.

The pressures at the inlet (d 1 ) and the outlet (d 2 ) are measured with two different piezometers. A piezometer is a device which uses hydrostatic pressure to measure pressure of a fluid. As shown in Figure I, a piezometer is a vertical tube attached to the pipe at the bottom and open to the atmosphere from the top. Using a set up like Figure I, the pressures at the inlet and throat can be calculated (or the difference in pressure) using two methods; hydrostatic equation and Bernoulli equation. Using the hydrostatic equation, the pressure at the inlet and throat can be obtained if the following values are known: atmospheric pressure (varies with temperature and altitude), gravity (varies with altitude), density of water (varies with temperature and altitude as well), and the height between the pipe and the water in the piezometer. p = patm + ρgh (1)

where ρ is the density of water, patm is the atmospheric pressure, g is the gravitational acceleration, and h is the distance between the pipe and the water in the piezometer. Using equation 1 for the pressure at the inlet and throat, values of p 1 (inlet) and p 2 (throat) are obtained. By subtracting the two equations, a value of the pressure difference is obtained: p 1 - p 2 = ρg (h 1 – h 2 ) (2)

If h 1 is greater than h 2 , then the pressure at the inlet (p 1 ) is higher than the pressure at the throat (p 2 ).

Equation 8 and 9 can be used to relate the velocity of the flow of fluid at the inlet and throat:

ρV 1 A 1 = ρV 2 A 2 (10) Where A is the cross-section area of the pipe at the inlet and throat. However, since the density is constant, and,

A = ❑ 4 D 2 (11)

Equation 10 becomes: V 1 DA2 = V 2 DD2 (12) And by definition, the volumetric flow rate is defined as, Q = VA (13)

By combing equations 2, 6, and 12 to solve for V 1 and then plugging it into equation 13, the theoretical volumetric flow rate is obtained:

Qtheo = ❑ 4 DA2DD

2 g(h 1 −h 2 ) D A 4 −D D 4

Finally, a ratio, called the discharge coefficient, is used to determine the losses due to viscosity and other things related to it in a flow system. And is defined as follows:

Cd = QtheoQact (15)

Procedure and Experimental Setup

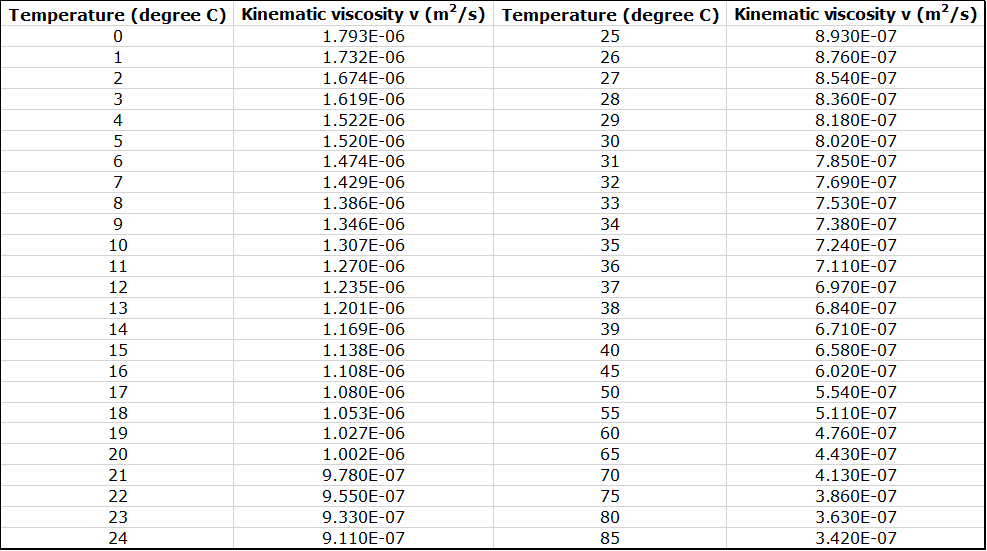
A water pump is connected to two parallel valves; one supplies water to the Venturi meter, while the other is a bypass valve which is used for safety measures in order not to damage any equipment. Water is then supplied and passes through the Venturi meter, and another hose leads the water into a measuring tank. On the Venturi meter, a set of eleven piezometers are placed along the pipe. The top of the piezometers is connected to a pressure manifold which allows the local pressure to be adjusted using a valve. Before starting the procedure, the piezometers must be leveled and air bubbles must be cleared, as they will change the height of the water in the piezometers and ultimately change the values of pressure and volumetric flow rate obtained. The control valve will be slowly closed to slowly increase the pressure which allows the water in the piezometers to rise and compress the air in the pressure manifold. Once the water has raised enough, the supply valve must be closed so the flow of water is stopped and static pressure is maintained. Opening one of the two valves will either increase or decrease the flow of water and alter the height difference between the inlet and throat. Also, water from the Venturi meter will be flowing through the pipe into a tank that stands on a scale. There will be six runs conducted with different heights between the inlet and throat.  Run 1: (hA – hD) = 10 inches  Run 2: 8 inches  Run 3: 6 inches  Run 4: 4 inches  Run 5: 2 inches  Run 6: 0 inches The heights of each of the eleven piezometers will be recorded. During each run, the flow rate is measured by collecting the water in the tank. A 15-pound weight will be placed and the water tank gate will be closed. When the lever of the scale becomes level, a timer will start to record the time it takes for the tank to be level with the scale. Then another 15-pound weight will be added and the time it takes the tank to level with the scale will be recorded. This will be repeated for five increments of 15-pound weights. Also, the temperature of the water must be recorded in order to obtain values for the density and viscosity of the water (used for volumetric flow rate, pressures, and Reynolds number). The temperature should be recorded after every run since the friction in the pipes could cause a temperature increase.

p = 103,812 Pa = 103 kPa The following equation was used to obtain the total head loss in meters from the inlet to the outlet.

HT = hA – hD + 8 Q

2 act ❑ 2 g

( D A 14 - D D 14 ) (18)

HT = 0 m Please note that all values used here were only obtained from the first run. The results for the other five runs can be found in the Results section. Next, we will use the values obtained for the volumetric flow rate for the six runs and compare it to their corresponding theoretical values. Using the following equation:

%error = actual theoretical−theoretical * 100 (19)

The following values for the actual volumetric are as follows for run one to six respectively, Qact = 4-4 m 3 /s Qact = 3 x10-4 m 3 /s Qact = 3 x10-4 m 3 /s Qact = 2 x10-4 m 3 /s Qact = 1 x10-4 m 3 /s Qact = 1 x10-4 m 3 /s And the following theoretical values for run one to six respectively, Qtheo = 4 x10-4 m 3 /s Qtheo = 3 x10-4 m 3 /s Qtheo = 3 x10-4 m 3 /s Qtheo = 2 x10-4 m 3 /s Qtheo = 1 x10-4 m 3 /s Qtheo = 1 x10-4 m 3 /s The following %error values are obtained: % error = -0% % error = -0% % error = -4% % error = -0% % error = -2% % error = -6%

Using the results obtained of the pressures and the height of the water in each piezometer, the following is generated,

1000000 2 4 6 8 10

Pressure vs Height

Run 1 Run 2 Run 3 Run 4 Run 5 Run 6

Height (in)

Pressure (Pa)

This graph represents the pressure distribution along the eleven of the piezometers. Since the slope is linear, the pressure is directly proportional to the height of the water in each piezometer tube. It may not be clearly visible, but the lowest pressure for each run was at the throat and the highest pressure at the inlet. This can be seen clearly using the table used to generate the graph found in the Appendix section.

The following results were obtained using equations 14, 15, 16, and 17 to generate Reynolds number and the discharge coefficient. Also, the following graph was generated to compare between the discharge coefficient and Reynolds number.

0 f(x) = 0 exp( 6786 x )

Volumetric Flow Rate vs Head Loss

Volumetric Flow Rate (m^3/s)

Head Loss (m)

This graph shows that the relationship between head loss and volumetric flow rate is exponential. This indicates that as the volumetric flow rate increases, the head loss will increase exponentially by a factor of 6,787. The trend-line reads as follows: y = 0.0025e6786 To sum up all the values obtained, Run hA – hD (m) Qact (m 3 /s) Qtheo (m 3 /s) Cd Re

####### 0 35526.

####### 0 31629.

Discussion and Conclusion

Throughout the experiment and obtaining the results it became evident that only two pressure taps, i. piezometer tubes are required to use a Venturi meter as a measuring device. The two piezometers or pressure taps need to be located at the inlet (first location on the pipe with the largest diameter) and throat (first location with the smallest diameter throughout the pipe). Two other devices used for flow measurement other than a Venturi meter are; orifice plates and pilot tubes. Orifice plates are used to measure fluid flow through the difference in pressure from the upstream side to the downstream of an obstructed pipe. The plate causing the obstruction allows for precise measurements because it narrowly constricts the fluid flow. However, at low flow rates, they become more inaccurate. In the case of pilot tubes, fluid flow is measured by converting the kinetic energy of the flow to potential. With the pilot probe, the dynamic pressure can be obtained. Throughout the experiment, it can be seen that at the throat of the Venturi meter the pressure deviates the most from the theoretical prediction. This occurs due to the Venturi effect which states that when a fluid flows through a narrower area, the fluid’s velocity increases while its static pressure decreases. The Venturi effect occurs to maintain the principle of continuity and the conservation of energy. Another topic is the effect of Reynolds number on the discharge coefficient. It can be seen from the graph that the relationship is rather cubic. An ideal experiment would yield a graph with a trend-line like the following: y = x 3 - x 2 + x. The result obtained was almost similar; y = 2 10-14x 3 – 1 10-9x 2 + 2*10-5x + 0. It can be seen that Reynolds number increases drastically while the discharge coefficient increases in increments of about 0. However, as Reynolds number lies between 20,000 and 30,000 the value of the discharge coefficient becomes stagnant. This shows that as flow becomes more turbulent, the viscous effects seem to wear off. Another conclusion drawn is that as Reynolds number decreases, the pressure distribution between the eleven piezometers also decreases. An example of this is for the first run, Reynolds number was calculated to be 35,526 and the pressure difference between the highest and lowest pressure points throughout the Venturi meter was 2,487 Pa. Reynolds number for run 4 was 22,531 and the pressure difference was only 994 Pa. Finally, regarding the relationship between head loss and flow rate, it can be seen from the graph that as the volumetric flow rate increases, the head loss increases exponentially at a rate of 6786.

Mayoral, Salvador, Ph., Flow Through a Venturi Meter, California State University Fullerton, Feb. 3, 2017

Pressure - -

• - 1 0 4- - 4- - 0 35526.
• 2 0 3. - x10- - 3. - x10- - 0 31629.
• 3 0 3. - x10- - 3. - x10- - 0 26465.
• 4 0 2. - x10- - 2. - x10- - 0 22531.
• 5 0 1. - x10- - 1. - x10- - 0 15565.
• 6 0 1. - x10- - 1. - x10- - 0 8179. - Time (s) Weight (lb) - 1 15 14 15 15 15. - 2 17 17 17 17 17. - 3 20 19 20 25 20. - 4 25 23 25 23 23. - 5 35 35 35 34 34. - 6 68 66 66 66 66.
• - 0. - - 0. - - 0. - - 0. - - 0. - - 0. - - 0. -
• - 9- - 0. - - 0. - - 0. - - 0. - - 0. - - 0. - - Run Cd Re - 0. - - 35526. - - - 0. - - 31629. - - - 0. - - 26465. - - - 0. - - 22531. - - - 0. - - 15565. - - - 0. - - 8179. -
• - 103128. -
• - 102879. -
• - 102630. -
• Multiple Choice

Course : Introduction to Engineering (ENGR A110)

University : orange coast college.

• Discover more from: Introduction to Engineering ENGR A110 Orange Coast College 13   Documents Go to course
• More from: Introduction to Engineering ENGR A110 Orange Coast College 13   Documents Go to course

Recommended for you

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Experiment #7: Osborne Reynolds’ Demonstration

1. introduction.

In nature and in laboratory experiments, flow may occur under two very different regimes: laminar and turbulent. In laminar flows, fluid particles move in layers, sliding over each other, causing a small energy exchange to occur between layers. Laminar flow occurs in fluids with high viscosity, moving at slow velocity. The turbulent flow, on the other hand, is characterized by random movements and intermixing of fluid particles, with a great exchange of energy throughout the fluid. This type of flow occurs in fluids with low viscosity and high velocity. The dimensionless Reynolds number is used to classify the state of flow. The Reynolds Number Demonstration is a classic experiment, based on visualizing flow behavior by slowly and steadily injecting dye into a pipe. This experiment was first performed by Osborne Reynolds in the late nineteenth century.

2. Practical Application

The Reynolds number has many practical applications, as it provides engineers with immediate information about the state of flow throughout pipes, streams, and soils, helping them apply the proper relationships to solve the problem at hand. It is also very useful for dimensional analysis and similitude.  As an example, if forces acting on a ship need to be studied in the laboratory for design purposes, the Reynolds number of the flow acting on the model in the lab and on the prototype in the field should be the same.

3. Objective

The objective of this lab experiment is to illustrate laminar, transitional, and fully turbulent flows in a pipe, and to determine under which conditions each flow regime occurs.

The visualization of flow behavior will be performed by slowly and steadily injecting dye into a pipe. The state of the flow (laminar, transitional, and turbulent) will be visually determined and compared with the results from the calculation of the Reynolds number.

5. Equipment

The following equipment is required to perform the Reynolds number experiment:

• F1-10 hydraulics bench,
• The F1-20 Reynolds demonstration apparatus,
• Cylinder for measuring flow,
• Stopwatch for timing the flow measurement, and
• Thermometer.

6. Equipment Description

The equipment includes a vertical head tank that provides a constant head of water through a bellmouth entry to the flow visualization glass pipe. Stilling media (marbles) are placed inside the tank to tranquilize the flow of water entering the pipe. The discharge through this pipe is regulated by a control valve and can be measured using a measuring cylinder [7]. The flow velocity, therefore, can be determined to calculate Reynolds number. A dye reservoir is mounted on top of the head tank, from which a blue dye can be injected into the water to enable observation of flow conditions (Figure 7.1).

Flow behavior in natural or artificial systems depends on which forces (inertia, viscous, gravity, surface tension, etc.) predominate. In slow-moving laminar flows, viscous forces are dominant, and the fluid behaves as if the layers are sliding over each other. In turbulent flows, the flow behavior is chaotic and changes dramatically, since the inertial forces are more significant than the viscous forces.

In this experiment, the dye injected into a laminar flow will form a clear well-defined line. It will mix with the water only minimally, due to molecular diffusion. When the flow in the pipe is turbulent, the dye will rapidly mix with the water, due to the substantial lateral movement and energy exchange in the flow. There is also a transitional stage between laminar and turbulent flows, in which the dye stream will wander about and show intermittent bursts of mixing, followed by a more laminar behavior.

The Reynolds number ( Re ), provides a useful way of characterizing the flow.  It is defined as:

The Reynolds number is a dimensionless parameter that is the ratio of the inertial (destabilizing) force to the viscosity (stabilizing) force. As Re increases, the inertial force becomes relatively larger, and the flow destabilizes and becomes fully turbulent.

The Reynolds experiment determines the critical Reynolds number for pipe flow at which laminar flow ( Re<2000  ) becomes transitional ( 2000<Re<4000  ) and the transitional flow becomes turbulent ( Re>4000 ). The advantage of using a critical Reynolds number, instead of critical velocity, is that the results of the experiments are applicable to all Newtonian fluid flows in pipes with a circular cross-section.

8. Experimental Procedure

Set up the equipment as follows:

• Position the Reynolds apparatus on a fixed, vibration-free surface (not on the hydraulics bench), and ensure that the base is horizontal and the test section is vertical.
• Connect the bench outflow to the head tank inlet pipe.
• Place the head tank overflow tube in the volumetric tank of the hydraulics bench.
• Attach a small tube to the apparatus flow control valve, and clamp it to a fixed position in a sink in the lab, allowing enough space below the end of the tube to insert a measuring cylinder. The outflow should not be returned to the volumetric tank since it contains dye and will taint the flow visualisation.

Note that any movement of the outflow tube during a test will cause changes in the flow rate, since it is driven by the height difference between the head tank surface and the outflow point.

• Start the pump, slightly open the apparatus flow control valve and the bench valve, and allow the head tank to fill with water. Make sure that the flow visualisation pipe is properly filled. Once the water level in the head tank reaches the overflow tube, adjust the bench control valve to produce a low overflow rate.
• Ensuring that the dye control valve is closed, add the blue dye to the dye reservoir until it is about 2/3 full.
• Attach the needle, hold the dye assembly over a lab sink, and open the valve to ensure that there is a free flow of dye.
• Close the dye control valve, then mount the dye injector on the head tank and lower the injector until the tip of the needle is slightly above the bellmouth and is centered on its axis.
• Adjust the bench valve and flow control valve to return the overflow rate to a small amount, and allow the apparatus to stand for at least five minutes
• Adjust the flow control valve to reach a slow trickle outflow, then adjust the dye control valve until a slow flow with clear dye indication is achieved.
• Measure the flow volumetric rate by timed water collection.
• Observe the flow patterns, take pictures, or make hand sketches as needed to classify the flow regime.
• Increase the flow rate by opening the flow control valve. Repeat the experiment to visualize transitional flow and then, at higher flow rates, turbulent flow, as characterized by continuous and very rapid mixing of the dye. Try to observe each flow regime two or three times, for a total of eight readings.
• As the flow rate increases, adjust the bench valve to keep the water level constant in the head tank.

Note that at intermediate flows, it is possible to have a laminar characteristic in the upper part of the test section, which develops into transitional flow lower down. This upper section behavior is described as an “inlet length flow,” which means that the boundary layer has not yet extended across the pipe radius.

• Measure water temperature.
• Return the remaining dye to the storage container. Rinse the dye reservoir thoroughly to ensure that no dye is left in the valve, injector, or needle.

9. Results and Calculations

Please visit this link for accessing excel workbook for this experiment.

The following dimensions of the equipment are used in the appropriate calculations. If required, measure them to make sure that they are accurate [7].

• Diameter of test pipe: d = 0.010 m
• Cross-sectional area of test pipe: A =7.854×10 -5 m 2

9.1. Results

Use the following table to record your measurements and observations.

Raw Data Table

9.2. calculations.

Calculate discharge, flow velocity, and Reynolds number ( Re ). Classify the flow based on the Re of each experiment. Record your calculations in the following table.

Result Table

Use the template provided to prepare your lab report for this experiment. Your report should include the following:

• Table(s) of raw data
• Table(s) of results
• A description, with illustrative sketches or photos, of the flow characteristics of each experimental run.
• How is the flow pattern of each of the three states of flow (laminar, transitional, and turbulent) different?
• Does the observed flow condition occur within the expected Reynold’s number range for that condition?
• Discuss your observation and any source of error in the calculation of the number.
• Compare the experimental results with any theoretical studies you have undertaken.

Applied Fluid Mechanics Lab Manual Copyright © 2019 by Habib Ahmari and Shah Md Imran Kabir is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book