make a table or an organized list problem solving

Fun teaching resources & tips to help you teach math with confidence

Math Strategies: Problem Solving by Making a List

As I’ve mentioned many times, one of the main goals in mathematics education is to raise up confident problem solvers . And while there are many ways to go about solving math problems, and we as adults may often see strategies as common sense, these are things that need to be taught. Giving kids as many tools as possible will set them up for success so that you can “let them loose” and see their creative minds work and explore. To continue my series on teaching kids to problem solve, today I’m going to discuss problem solving by making a list .

–>Pssst! Do your kids need help making sense of and solving word problems? You might like this set of editable word problem solving templates ! Use these with any grade level, for any type of word problem :

Making a Meaningful List: 

This was always a hard approach for me personally because it doesn’t seem like math, and can often be time consuming. I mean, who really wants to sit and list out all the possible solutions to a math problem? BUT, it is a very useful strategy, and as we’ll see, learning to be organized and systematic is the key ( and will also save tons of time )!

So when is it useful to make a list? Basically, any time you have a problem that has more than one solution , or you’re trying to solve a combination problem , it’s helpful to make a list.

But not just any list of possibilities. That will feel useless and frustrating if you’re just trying to pull out possibilities from anywhere. And more than that, it’s very likely possibilities will be skipped or repeated, making the final solution wrong.

On top of that, it will probably be more time consuming to make a list if you don’t have a systematic approach to it, which is probably why I was never a fan as a kid. No one wants to just sit and stare at the paper hoping solutions will pop into their brain.

Organizing the information in a logical way keeps you on track and ensures that all the possible solutions will be found.

There are different ways to organize information, but the idea is to exhaust all the possibilities with one part of your list before moving on.

For example, say you’re trying to figure out all the different combinations of ice cream toppings at your local ice cream shop. They have 3 different flavors (chocolate, vanilla and strawberry), but also have 4 different toppings (nuts, whipped cream, chocolate candies and gummy bears).

If you just start listing different possibilities without any kind of structure, you’re bound to get lost in your list and miss something. So instead, list all the possibilities for chocolate ice cream before moving on to vanilla.

Chocolate: just chocolate (no toppings), chocolate with nuts, chocolate with whipped cream, chocolate with candies and chocolate with gummy bears.

Now we see that there are 5 possibilities if you get chocolate ice cream, and so we can move on to vanilla, and then strawberry.

The key is to start with the first flavor and list every possible topping in order . Then move on to the next flavor and go through the toppings in the same order .

Then nothing gets skipped, forgotten or repeated . After completing the list, we see that there are 15 possible combinations.

Some students may even notice that there will be 5 possibilities for each flavor , and thus multiply 3×5 without completing the list. (That’s another great strategy: look for patterns ).

Even if a pattern is not discovered, however, completing the list in an organized, systematic way will ensure all possibilities are covered and the total (15) found.

Another way to organize the list is to make a tree diagram . Here’s another example problem:

Sarah is on vacation and brought 3 pairs of pants (blue, black, and white) and 3 shirts (pink, yellow and green). How many different outfit combinations can she make?

Using a tree diagram is a great way to keep the information organized, especially if you have kids who struggle with keeping track of their list:

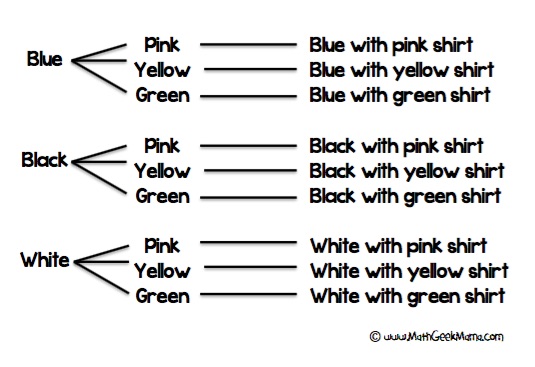
Then it is very easy for students to see that there are 9 different outfit combinations .

Was this helpful? Is it a strategy that you share with your kids?

See the rest of the posts in this series and prepare your kids to be great problem solvers:

• Problem Solve by Solving an Easier Problem
• Problem Solve by Drawing a Picture
• Problem Solve by Working Backwards
• Problem Solve by Finding a Pattern
• Problem Solve with Guess & Check

I’m really liking this “problem solving” series! As someone who’s not so great as problem solving, these tips are going to come in handy when helping my daughter! Thanks for sharing at the Thoughtful Spot!

I was never very good at math, and unfortunately, my daughter isn’t great at it either. I came across this post on Hop (on the Hip Homeschool Moms site), and I love it! I’m going to read the other articles in the series too. I would love to help my daughter enjoy and understand math, and I’m hopeful that your posts will help me do that! Thanks so much for sharing your post with us on the Hop!

Comments are closed.

Similar Posts

“2×2=BOO!” Hands-On Multiplication Fun!

Disney Math: Using Pattern Blocks to Create Cinderella’s Castle!

The Best Books to Teach Addition and Subtraction

Weekly Math Freebie Round Up

Christmas Shopping: Money Math Practice {FREE}

Understanding the Distributive Property {FREE Lesson!}

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Problem Solving: Make a Table Math Strategy

Math Problem Solving: Make a Table

In this introductory guide, we will explore the Make a Table math strategy, a valuable tool for solving problems by organizing information in a logical format.

This problem-solving strategy encourages students to identify patterns and relationships within data. We’ll explain the strategy using an example and explain how it can be used effectively in mathematical problem-solving.

What is the Make a Table Math Strategy?

Making a table is a math problem-solving strategy that students can use to solve  word problems  by writing information in a more organized format.

Example of a problem that can be solved by making a table:

Juanita checked a book out of the library, and it is now 7 days overdue. If a book is 1 day overdue, the fine is 10¢, 2 days overdue, 20¢, 3 days overdue, 30¢, and so on. How much is her fine?

Why is the Make a Table Math Strategy Important?

This problem-solving strategy allows students to discover relationships and patterns among data. It encourages students to organize information logically and to look critically at the data to find patterns and develop a solution.

How to Make a Table to Solve a Math Problem

To help you learn to teach the Make a Table Math strategy, we will use the following word problem as an example:

How many hours will a car traveling at 65 miles per hour take to catch up with a car traveling at 55 miles per hour if the slower car starts one hour before the faster car?

Step 1: Understand the Problem

Demonstrate that the first step is understanding the problem. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words.

In this problem, students need to understand that there is a slower car going 55 miles per hour and a faster car going 65 miles per hour. The slower car starts one hour before the faster car. Students need to find how many hours it will take the faster car to catch up to the slower car.

Step 2: Choose a Strategy

Because there are three sets of data to organize, you should use the Make a Table strategy. Generally, if there is data associated with a certain category, it can be organized easily by making a table. This strategy also overlaps with the  Find a Pattern strategy  because it is often easier to find a pattern when the data is organized in a table.

Step 3: Solve the Problem

Make a table to organize the data. For this example, create a row for the slower car, a row for the faster car, and a column for each hour. Find the distance traveled during each hour by looking at the distances listed in each column.

The distance of the faster car was more than the distance of the slower car in hour seven. The faster car took six hours to catch up to the slower car.

Step 3: Check Your Work

Reread the problem to be sure the question was answered.

Did you find the number of hours it took for the faster car to catch up?

Yes, it took 6 hours.

Check the math to be sure it is correct.

55 x 2 = 110, 55 x 3 = 165, 55 x 4 = 220, 55 x 5 = 275, 55 x 6 = 330, 55 x 7 = 385 65 x 2 = 130, 65 x 3 = 195, 65 x 4 = 260, 65 x 5 = 325, 65 x 6 = 390

Determine if the best strategy was chosen for this problem or if there was another way to solve the problem.

Making a table was a good way to solve this problem.

Step 4: Explain Your Work

The last step is explaining how you found the answer. Demonstrate how to write a paragraph describing the steps you took and how you made decisions throughout the process.

I set up a table for the miles each car had gone during each hour. I kept adding columns until the faster car caught up to the slower car. At the end of the seventh hour, the faster car had gone 390 miles, which was more than the distance traveled by the slower car, 385 miles. Because the faster car didn't start traveling in the first hour, it traveled for six hours.

Step 5: Guided Practice

Have students try solving the following problem using the strategy Make a Table.

The printer in the media center can print 1 page every 30 seconds. The printer in the office can print 4 pages every 30 seconds. If both printers are printing, how many pages will the office printer have printed by the time the media center printer prints 5 pages?

Have students work in pairs, groups, or individually to solve this problem. They should be able to tell or write about how they found the answer and justify their reasoning.

How Can You Stretch Students’ Thinking?

The Make a Table math strategy can be stretched when combined with other strategies, such as looking for patterns or drawing a picture. By combining this strategy with others, students can analyze the data that is given to find more complex relationships.

The full page is available ONLY to subscribers. Sign up today to get access to this page and all of the content on TeacherVision®.

Featured Middle School Resources

Elements of Poetry Workbook

Use this poetry toolbox workbook to support your students to learn different poetic terms and devices, and then practice...

Earth Day Activities: History of Earth Day Reading Passage and Quiz

Help your students work on their reading comprehension skills while learning all about Earth Day with this reading compr...

Test Prep Strategies, Tools, and Practice Questions

Help set your students up for academic success with this packet of test-taking tips, test preparation strategies, and pr...

Related Resources

TEACHING RESOURCE

Pattern Problem Solving: Teach Students to Find a Pattern in Math Problems

Pattern problem solving In this article, we’ll delve into the concept of pattern problem solving, a fundamental mat...

Math Problem Solving: The Guess and Check Method

Math Problem Solving: The Guess and Check Method In this article, we will explore the guess and check method, a power...

Problem Solving: Draw a Picture

Problem Solving: Draw a Picture What Is It? The draw a picture strategy is a problem-solving technique in which students...

Problem Solving: Choose the Operation

Problem Solving: Choose the Operation What Is It? The process of "choosing the operation" involves deciding which mathem...

Problem Solving: Eliminating Possibilities

Problem Solving: Eliminating Possibilities What Is It? Eliminating Possibilities is a strategy in which students remove ...

Problem Solving: Simplify the Problem

Problem Solving: Simplify the Problem What Is It? Simplifying a mathematics problem is a strategy that often is used alo...

About the author

Haley Horton

Digital content manager & editor, about haley.

My Learning Springboard

School Planning | Academic Tutoring | Test Preparation

A Multidisciplinary Educational Consulting Firm

More results...

Problem-Solving Strategies

January 26, 2021 Brad Hoffman Leave a Comment

Certainly, many students find that it is possible to solve a given word problem with minimal consideration of how to approach it. People have varying degrees of “math sense.” Some find most math problems mysterious. Some, however, can very easily see what to do to find solutions; it almost seems obvious to them. But even for students with strong “math sense,” there come those situations when they don’t intuitively know what to do. For all learners, the recognition of specific problem-solving strategies to solve math problems is useful. Thinking about our own thinking (aka metacognition) is important in developing flexibility so that we can see more than one way to solve a particular problem. Math journaling supports this thinking and development.

Below you will find a list of some very useful problem-solving strategies . One thing that is particularly beneficial about this set of strategies is that they are, in fact, universal. In other words, they will work regardless of the math program a student might be using. Whether it’s Singapore Math or Everyday Math or something else entirely , these problem-solving strategies can provide a clear path toward solutions. Interestingly, they can even extend to problem-solving outside the area of math! Becoming familiar with them and comfortable using them can be a big help to students as they wend their way through problems, be they less or more complex.

10 Problem-Solving Strategies

• Make a model/Act out
• Draw a diagram or picture
• Look for a pattern
• Make an organized list
• Make a table
• Guess & Check
• Make it simpler
• Work backwards
• Use logical reasoning

Here are some examples of problems and how to use these strategies.

“How many complete turns does the hour hand on a clock make in one day?”

From the list of problem-solving strategies above, “make a model or act it out” is an excellent choice for this problem. A student could use a model or a real analog clock and turn the hands and count. Distinguishing between the minute and the hour hand and recognizing that the clock only shows 12 of the 24 hours in a day lets the student see that the hour hand makes two complete turns. A physical clock that a student can actually turn provides an important concrete experience that may prove helpful for finding the solution.

“Using each of the digits 0, 1, 2, 3, 4 only once, make a two-digit number times a three-digit number multiplication problem with the greatest product.”

Students can “ draw a diagram or picture” of an “empty” multiplication problem with a box for each digit. Consider which two digits give the largest product and put them in the highest place value spots. Then, if it’s not immediately evident to the student, use one of the other problem-solving strategies — “ guess and check” — to place the remaining digits in the remaining spots. Check by multiplying the results to identify which is actually the largest (e.g. Is it 430 x 21 or 320 x 41?)

“How many even numbers are there between 201 and 351?”

In this instance, “ look for a pattern” would be especially helpful from the list of problem-solving strategies. Either write all numbers from 201 through 351 and notice the pattern that there are 5 in every set of 10 numbers (e.g. 201-210), and then count how many sets of 10 numbers there are and multiply that by 5, or simply write one set of 10 numbers and identify the 5 in 10 pattern without writing out all of them. Either way is valid.

“You have two noses and three hats. How many different nose-hat disguises can you wear?”

For this problem, “ make an organized list ” from the problem-solving strategies listed above works well. The list will start with Hat A and match with each nose (2), then Hat B with each nose (2), then Hat C with each nose (2). This gives a total of 6 disguises.

“How many numbers between 10 and 30 give a remainder of 2 when divided by 3?” You could “ make a table” to find the solution.

As the Table continues, a pattern becomes evident (“ look for a pattern ” — overlapping strategy!) in which every third number gives a remainder of 2. Count them for a solution.

“If 25 Glinks equal a Glonk, and 15 Glonks equal a Glooie, how many Glinks equal 2 Glooies?”

Please, “ make it simpler”! That strategy is an especially good choice from the list of problem solving-strategies. Let’s look at a simpler, but similar, problem. It’s simpler because the numbers are smaller, and you could even draw a picture to prove it’s correct.

If 3 Glinks equal a Glonk. And 2 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 3×2, which equals 6.

So, if 6 Glinks equal a Glooie, then how many Glinks equal 2 Glooies? Multiply 6×2, which equals 12. So, 12 Glinks equal 2 Glooies.

Now with the larger numbers:

If 25 Glinks equal a Glonk. And 15 Glonks equal a Glooie. How many Glinks equal a Glooie? Multiply 15×25, which equals 750. So, 750 Glinks equal a Glooie.

Then, how many Glinks equal 2 Glooies? Multiply 750×2, which equals 1500. So, there are 1500 Glinks in 2 Glooies.

It’s the same process, with bigger numbers! Much simpler!

“If I add 10 to my age and double it, I am 90. How old am I?”

From the list of problem-solving strategies, this problem begs for the student to “ work backwards”. Simply un-double the 90 and subtract ten. 90 divided by 2 = 45 and 45-10=35. Voilà! The answer is 35 years old! Then reverse again to confirm that the answer is correct.

“Arrange these digits and symbols to make a true number sentence (equation.) 3,1,4,9,+,/,= (Note: the forward slash  [/] signifies “divided by”.)

“ Use logical reasoning ” to realize that any order is possible, but a larger number needs to be divided by a smaller number with no remainder (9/3=3) Then 3+1=4, so the sentence 9/3+1=4 is the solution.

For the problems that seem absolutely impossible to solve, your best option is to “ brainstorm” , and that’s on the above list of problem-solving strategies! Try various ideas; work with a partner; explore to see what might work; try everything you can think of! It’s amazing how good ideas will sometimes just pop into one’s head!

As a student works with these problem-solving strategies, it becomes clear that they often overlap (as in the “ draw a picture” / “guess and check” example above, problem #2). Or a student becomes especially attached to a few particular strategies that often work well. Some problems seem to be especially suitable for a particular strategy, while others can be approached from several directions. Having the flexibility to move from one strategy to another helps avoid the serious “I’m STUCK!” situation. Also, using more than one strategy on the same problem allows students to check solutions more efficiently before moving on. Again, however, THINKING about how we are THINKING is very beneficial in developing skills in this area. We call this metacognition .

Solving word problems can be fun, like being a detective who has unusual insight. There are solutions! Enjoy finding them! And make effective use of problem-solving strategies!

By Jean Snyder and Brad Hoffman , Elementary Math Specialists

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Notify me of follow-up comments by email.

Notify me of new posts by email.

Company Overview

School Planning

Private Tutoring

Test Preparation

Strategy: Making & Using a Table

Math Problem Solving Strategy: Making and Using a Table to Solve a Problem

This is another free resource for teachers from The Curriculum Corner.

Looking to help your students learn to make a table to solve a problem?

This math problem solving strategy can be practiced with this set of resources.

Math Problem Solving Strategies

This is one in a series of resources to help you focus on specific problem solving strategies in the classroom.

Within this download, we are offering you a range of word problems for practice.

Each page provided contains a single problem solving word problem.

Below each story problem you will find a set of four steps for students to follow when finding the answer.

This set will focus on the make a table strategy for math problem solving.

What are the 4 problem solving steps?

After carefully reading the problem, students will:

• Step 1:  Circle the math words.
• Step 2:  Ask yourself: Do I understand the problem?
• Step 3:  Solve the problem using words and pictures below.
• Step 4:  Share the answer along with explaining why the answer makes sense.

Making & Using a Table to Solve Problems

 This set of problems assumes children have already had instruction on how to create a table to organize their information. 

The problems give them different scenarios and the students have to organize the information in their own tables in order to solve the problems. 

If you have students who still need additional support, we have provided pages with the table already added to get them started. 

For even more support, you could add some starting information in the table. 

As always, we feel its important to differentiate for the needs of individuals or groups in your classrooms.

You can download this set of making and using tables to solve problems practice here:

Problem Solving

You might also be interested in:

• Problem Solving Strategies & Anchor Chart
• Problem Solving Challenge

As with all of our resources, The Curriculum Corner creates these for free classroom use. Our products may not be sold. You may print and copy for your personal classroom use. These are also great for home school families!

You may not modify and resell in any form. Please let us know if you have any questions.

The answer is... Problem Solving Center - The Curriculum Corner 4-5-6

Thursday 30th of January 2020

[…] Making & Using a Table […]

Strategy: Making Change - The Curriculum Corner 4-5-6